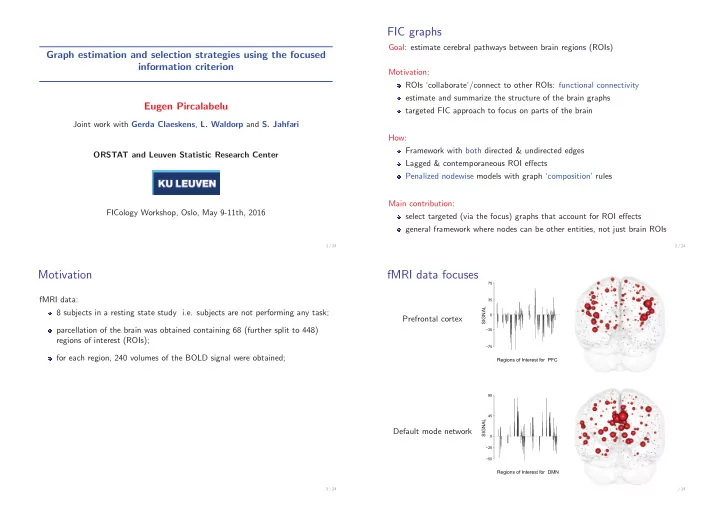
FIC graphs Goal: estimate cerebral pathways between brain regions - PowerPoint PPT Presentation

FIC graphs Goal: estimate cerebral pathways between brain regions (ROIs) Graph estimation and selection strategies using the focused information criterion Motivation: ROIs ‘collaborate’/connect to other ROIs: functional connectivity estimate and summarize the structure of the brain graphs Eugen Pircalabelu targeted FIC approach to focus on parts of the brain Joint work with Gerda Claeskens , L. Waldorp and S. Jahfari How: Framework with both directed & undirected edges ORSTAT and Leuven Statistic Research Center Lagged & contemporaneous ROI effects Penalized nodewise models with graph ‘composition’ rules Main contribution: FICology Workshop, Oslo, May 9-11th, 2016 select targeted (via the focus) graphs that account for ROI effects general framework where nodes can be other entities, not just brain ROIs 1 / 24 2 / 24 Motivation fMRI data focuses 75 fMRI data: 35 SIGNAL 8 subjects in a resting state study i.e. subjects are not performing any task; 0 Prefrontal cortex parcellation of the brain was obtained containing 68 (further split to 448) −35 regions of interest (ROIs); −75 for each region, 240 volumes of the BOLD signal were obtained; Regions of Interest for PFC 90 45 SIGNAL Default mode network 0 −25 −50 Regions of Interest for DMN 3 / 24 4 / 24

Prefrontal cortex focused graph Graph theoretical framework Define the graph G = ( E , V ) based on edges E nodes V r.v X i : i ∈ V . To each X 1 . . . X p a node in V = { 1 . . . p } is associated. E a subset of V × V set of pairs of distinct nodes. ( i , j ) ∈ E i → j i parent of j ( j , i ) ∈ E j → i i child of j ( j , i ) ∪ ( i , j ) ∈ E i − j i neighbor of j One or more connections between i and j (directed/undirected); Self-loop edges are allowed (such as i → i ) and denote a lagged effect. 5 / 24 6 / 24 Graph selection procedures Proposed method Graphical Lasso: undirected edges 1 the ‘best graph’ should depend on the focus Σ − 1 ≻ 0 (log det Σ − 1 − tr( W Σ − 1 ) − λ || Σ − 1 || 1 ) max for different focuses, possibly different selected models the focus guides the graph selection aspect ∈ E ≡ Σ − 1 X i ⊥ X j | X { 1 ,..., p }\{ i , j } iff ( i , j ) ∪ ( j , i ) / = 0 ij Gaussian AR model; Neighborhood selection: undirected edges 2 penalized nodewise neighborhood selection; X i ⊥ X k | X ne i ∀ i ∈ V & ∀ k ∈ V \ { ne i ∪ i } mean squared error (MSE) to decide on the selection; X i ‘response node’, other X j ( j � = i ) covariates in a linear regression. Lasso reg. to determine the neighborhood of node i Let { j ∈ V : ˆ Y ≡ X i : i ∈ V the node of interest. ne λ θ i ˆ = j � = 0 } i E λ, AND ˆ ne λ ne λ W ≡ set of protected nodes, always included as neighbors of Y = { ( i , j ) : i ∈ ˆ j AND j ∈ ˆ i } E λ, OR ˆ ne λ ne λ = { ( i , j ) : i ∈ ˆ j OR j ∈ ˆ i } Z ≡ set of unprotected nodes, potential neighbors Time Series Chain Graphical Models (TSCGM): undirected+directed edges 3 Subset S ⊆ V \ i of possible neighbors is to be selected. X t | X t − 1 ∼ N (Γ X t − 1 , Σ) . 7 / 24 8 / 24

Local misspecification Penalty function Penalty needed for parameter estimation in p > n settings. FIC takes care of selection so sparse penalties are not necessary. Y k has density f ( y k | w k , z k , θ 0 , γ 0 + δ/ √ n ) for k = 1 , . . . , n Local quadratic approximation to ψ when not differentiable at zero. lasso : ψ l ( | γ j − γ j 0 | ) = | γ j − γ j 0 | f is 2 times diff. in a ‘proximity’ of ( θ 0 , γ 0 ) adaptive lasso : ψ al ( | γ j − γ j 0 | ) = w j | γ j − γ j 0 | , for a weight w j bridge : ψ b ( | γ j − γ j 0 | ) = | γ j − γ j 0 | α α > 0 ( θ 0 , γ 0 + δ/ √ n ) hard thresholding : ψ h ( | γ j − γ j 0 | ) = λ 2 − ( | γ j − γ j 0 | − λ ) 2 I ( | γ j − γ j 0 | < λ ) δ controls the proximity around narrow model ′ SCAD : ψ s ( | γ j − γ j 0 | ) = I ( | γ j − γ j 0 | ≤ λ )+ w k protected neighbors ⇒ θ is present in all models (never subject to model ( a λ − | γ j − γ j 0 | ) + I ( | γ j − γ j 0 | > λ ); a > 2 . selection or exclusion) ( a − 1) λ ′ ( | γ japx | ) ψ ( | γ j − γ j 0 | ) ≈ ψ ( γ japx ) + 1 ψ ( γ j − γ j 0 ) 2 − γ 2 � � d γ japx � n � 2 | γ japx | 1 log f ( y k | w k , z k , θ, γ ) − λ (ˆ � � θ, ˆ γ ) = arg max ψ ( | γ j − γ j 0 | ) , ′ ( | γ japx | ) n n ′ ≈ ψ θ,γ k =1 j =1 ψ ( | γ j − γ j 0 | ) ( γ j − γ j 0 ) | γ japx | for a given penalty function ψ (2 times diff. in 0) and an external value λ . ′ ( | γ japx | ) ′′ ≈ ψ ψ ( | γ j − γ j 0 | ) | γ japx | 9 / 24 10 / 24 Selecting λ Focus parameters Define a focus parameter µ = µ ( θ, γ, w , z ) a function of θ and γ . � � ω T { J 11 , S , 0 cc T ( J 11 , S , 0 ) t − 2( I − G S ) δ c T ( J 11 , S , 0 ) T } ω min c µ ( σ, β, w , z ) = [ w , z ] t β ; mean of a ROI for fixed vals of other ROIs Eg: For ROI 1 k we define the focus, as the conditional mean on covariates √ n z = ( ROI 2 k , ROI 3 k , ROI 4 k , ROI 1 k − 1 , ROI 2 k − 1 , ROI 3 k − 1 , ROI 4 k − 1 ) as λ S = ω T ( I − G S ) δ 1 q T ( J 11 , S , 0 ) T ω ψ ′′ (0) . ω T J 11 , S , 0 1 q 1 q T ( J 11 , S , 0 ) T ω µ = E [ ROI 1 k | z = ( − 20 , 100 , 25 , 45 , 80 , 10 , 50)] µ ( σ, β, w , z ) = β l ; reg.coef of a certain ROI l Endogeneity problem: MSE ≻ c ≻ λ ≻ ( θ, γ ) ≻ λ Two-step solution: estim. ( θ, γ ) on a λ grid, retain (ˆ θ, ˆ γ ) with best GCV µ ( σ, β, w , z ) = G − 1 (0 . 9 | w , z ); 0.90-quantile of the response distribution at performance, estimate c and based on c estimate MSE fixed vals for other ROIs. Goal: estimate µ as precisely as possible (in the MSE sense). 11 / 24 12 / 24

Limiting distribution Graph composition rules For any model S , we compute Once all nodewise models are selected (some might include only contemporaneous √ n (ˆ d or only dynamic effects, while others might contain both) we apply the ‘OR’ rule µ S − µ true ) → Λ S ∼ N (Bias( µ, S , δ, c ) , Var( µ, S )) , µ S ) = Bias( µ, S , δ, c ) 2 + Var( µ, S ) . MSE(ˆ � � E λ, or ˆ ne λ ne λ = ( i , j ) ∪ ( j , i ) : i k ∈ ˆ j k or j k ∈ ˆ instantaneous undirected i − j i k p � � � E λ, or ˆ � ne λ FIC( G ( E S , V )) = MSE(ˆ µ l ; S l ) , = ( i , j ) : i k − 1 ∈ ˆ lag 1 directed i → j j k l =1 � � E λ, or ˆ ne λ = ( j , i ) : j k − 1 ∈ ˆ lag 1 directed i k i ← j where S = { S 1 , . . . , S p | S 1 ⊆ { V \ 1 } ; . . . ; S p ⊆ { V \ p }} . � � ˆ E λ, or ˆ ∪ ˆ E λ, or i → j ∪ ˆ E λ, or E λ, or = directed and undirected i − j i ← j ne λ denotes the neighborhood of the considered node for a certain value of where ˆ The mean depends on the chosen focus µ , the submodel S , the value of δ the penalty. indicating the distance between the parameters from the simplest model and the ′′ (0)1 q / √ n . true model, and on the chosen penalization via the value c = λψ 13 / 24 14 / 24 Prefrontal cortex and Default mode network as focuses Focus FIC LQA ℓ 1 FIC ℓ 2 Ratio vs FIC GL-CV(Lik) GL-StARS MSPE (PFC focus) 1.52 1.11 MSPE (DMN focus) 1.44 1.06 No. of edges (PFC focus) 4.67 10.3 No. of edges (DMN focus) 4.40 9.70 Table: Ratios of the empirical MSPE and number of edges in the estimated graphs for GL-CV(Lik) and GL-StARS relative to the graphs estimated using FIC - LQA ℓ 1 for the PFC and DMN focuses. 15 / 24 16 / 24