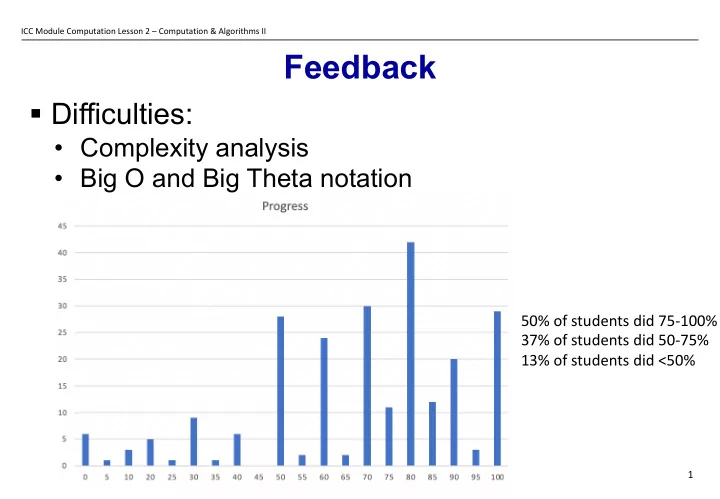

ICC Module Computation Lesson 2 – Computation & Algorithms II Feedback § Difficulties: • Complexity analysis • Big O and Big Theta notation 50% of students did 75-100% 37% of students did 50-75% 13% of students did <50% 1
ICC Module Computation Lesson 2 – Computation & Algorithms II Information, Computation, and Communication Algorithm 2 2
ICC Module Computation Lesson 2 – Computation & Algorithms II Topics § Recursion § Complexity of a recursive algorithm § Dynamic Programming § (Binary Search « Recherche dichotomique ») 3
Understanding a Recurive Algorithm What is the output if L={5,8,6,10,3}? A. 5 B. 8 C. 24 D. 32
ICC Module Computation Lesson 2 – Computation & Algorithms II Complexity Height? Cost? Algo1({5,8,6,10,3}) ∼ 10 --”-- Algo1({8,6,10,3}) --”-- Algo1({6,10,3}) n+1 Algo1({10,3}) --”-- Algo1({3}) --”-- Algo1({}) 3 T(n)=10 ・ n + 3 = Θ(n) 5
ICC Module Computation Lesson 2 – Computation & Algorithms II Writing a Recursive Algorithm § Find the largest number in a list • Input: a list L with n numbers • Output: the largest number in this list § Idea of recursion: • Use a solution of a smaller problem (a shorter list) § You need to answer two questions: 1. Assume we are given the largest element in the list L[2:n] (list of length n-1), how would we compute the largest element of the list L[1:n]? 2. What is the termination condition? What is the largest element of a list of size 1? 6
ICC Module Computation Lesson 2 – Computation & Algorithms II Question 1: from n-1 to n 7
ICC Module Computation Lesson 2 – Computation & Algorithms II Question 2: Termination 8
Find Max (Recursively) What is the complexity of this algorithm? A. Θ(log(n)) B. Θ(n) C. Θ(n 2 ) D. Θ(2 n )
ICC Module Computation Lesson 2 – Computation & Algorithms II Complexity Height? Cost? rec_max({5,8,6,10,3}) ∼ 8 --”-- rec_max({8,6,10,3}) --”-- rec_max({6,10,3}) n+1 --”-- rec_max({10,3}) Rec_max({3}) --”-- 3 T(n)= 8 ・ n + 3 = Θ(n) 10
ICC Module Computation Lesson 2 – Computation & Algorithms II Recursion or Not? § The recursive solution is not always the only solution and rarely the most efficient ... § ...but it is sometimes much simpler and more practical to implement ! § Examples : sorting, processing of recursive data structures (e.g. trees, graphs, ...), ... 11
ICC Module Computation Lesson 2 – Computation & Algorithms II Fibonacci Numbers (Recursive Version) F(n) = F(n-1) + F(n-2) for n>1 F(0) = 0 et F(1) = 1 Month 1: 1 Month 2: 1 Month 3: 2 Month 4: 3 Month 5: 5 Month 6: 8 Named after Leonardo Fibonacci (1175-1250) 12
ICC Module Computation Lesson 2 – Computation & Algorithms II Fibonacci Numbers in Nature The lengths of the Number of ancestors squares describing 13 of a drone (a male naturally appear honey bee) is a spirals are often 2 3 Fibonacci number. 8 1 1 Fibonacci numbers. 5 In these pictures there are 55 curves of seeds spiraling to the left as you go outwards and 34 spirals of seeds spiraling to the right. A little further towards the center you can count 34 spirals to the left and 21 spirals to the right. These pairs of numbers are (almost always) neighbors in the Fibonacci series. https://plus.maths.org/content/life-and-numbers-fibonacci 13
ICC Module Computation Lesson 2 – Computation & Algorithms II Fibonacci Recursive F(n) = F(n-1) + F(n-2) for n>1 Height? Cost? F(0) = 0 et F(1) = 1 1 F(5) = F(4)+F(3) F(4) = F(3)+F(2) F(3) = F(2)+F(1) 2 4 F(3) = F(2)+F(1) F(2) = F(1)+F(0) F(2) = F(1)+F(0) F(1) 6 F(2) = F(1)+F(0) F(1) F(1) F(0) F(1) F(0) 2 F(1) F(0) In each box in this tree we have to performance a constant number of instructions. $ 2 ! = 2 $%& − 1 = 𝑃(2 $ ) 1. How many boxes (function calls) are in this tree? < " !"# 2. How high is the tree? The height is n $%& 14 ' 2 ! = 2 $(& $ ' − 1 = Ω(2 > " ' ) !"#
ICC Module Computation Lesson 2 – Computation & Algorithms II Fibonacci Recursive § Complexity F(n)? Exponential in n § Is there a better solution? Idea : do not perform the same calculation many times but store the already calculated value for later use 15
ICC Module Computation Lesson 2 – Computation & Algorithms II Dynamic Programming § Dynamic programming is strategy to solve problems. • It applies to problems for which we can find an optimal solution by breaking it down into smaller optimal overlapping sub-problems in a recursive manner. • To solve such problems efficiently we memorize the solutions of sub-problems to avoid re-computation. § If the sub-problems are not overlapping the solving strategy is called ” divide and conquer ” (like in binary search « Recherche dichotomique »). 16
ICC Module Computation Lesson 2 – Computation & Algorithms II Dynamic Programming - Fibonacci Memoize the last two computations (x and y) 17
Complexity? A. Θ(log n) B. Θ(n) C. Θ(n 2 ) D. Θ(2 n )
ICC Module Computation Lesson 2 – Computation & Algorithms II Dynamic Programming – Floyd Computation of the shortest path , for example between all the train stations of the CFF network. Given a graph G with vertices 1,2,..,N, consider a function called D k-1 (i,j) that returns the shortest path from i to j using only vertices Zürich from 1 to k-1 as intermediate points . j Biel Key Idea of the algorithm: k-1 The shortest path to go from i to j (e.g., Lausanne D k-1 (i,j) to Zürich) is the shortest among: D (k,j) k-1 1. The shortest known path from Lausanne to Bern k Zürich, 2. The path from Lausanne to Zürich by traversing a city not known yet (e.g., Bern) D (i,k) k-1 D k ( i, j ) = min {D k − 1 ( i, j ) , D k − 1 ( i, k ) + D k − 1 ( k , j ) } i 19 Lausanne
ICC Module Computation Lesson 2 – Computation & Algorithms II Dynamic Programming – Floyd 20
ICC Module Computation Lesson 2 – Computation & Algorithms II Floyd’s Algorithm: Example Lausanne Biel Bern Zürich D(i,j) Zürich 0 133 58 ∞ Lausanne Biel 4 38 133 0 45 38 Biel 2 58 45 0 102 Bern ∞ 38 102 0 Zürich 102 45 Bern 3 133 58 1 Going throw (1) Lausanne does not give any improvements. Lausanne Going throw (2) Biel improves the distances (fictitious data) from Lausanne to Zürich and • 21 • from Zürich to Bern
ICC Module Computation Lesson 2 – Computation & Algorithms II Floyd’s Algorithm: Example Lausanne Biel Bern Zürich Zürich 0 133 58 ∞ Biel 4 38 D 0 = D 1 133 0 45 38 2 58 45 0 102 ∞ 38 102 0 102 45 Lausanne Biel Bern Zürich Bern 3 133 0 133 0 D 2 = 58 45 0 58 171 38 83 0 1 Going throw (1) Lausanne does not give any improvements. Lausanne Going throw (2) Biel improves the distances (fictitious data) from Lausanne to Zürich and • 22 • from Zürich to Bern
ICC Module Computation Lesson 2 – Computation & Algorithms II Floyd’s Algorithm: Example Lausanne Biel Bern Zürich Zürich 0 Biel 4 38 133 0 D 2 = 2 58 45 0 171 38 83 0 102 45 Lausanne Biel Bern Zürich Bern 3 133 0 103 0 D 3 = 58 45 0 58 141 38 83 0 1 Going throw (3) Bern improves the distances Lausanne • from Lausanne to Biel and (fictitious data) from Zürich to Lausanne • Note: it also works for asymmetric 23 Going throw (4) Zürich does not give any improvements graphs (directed graphs)
Complexity? Θ(n 2 ) A. Θ(n 3 ) B. Θ(n 4 ) C. Θ(n 5 ) D.
ICC Module Computation Lesson 2 – Computation & Algorithms II Conclusion § There is no miracle recipe to find an algorithm, but there exist big families of resolution strategies: • decompose (e.g., “recursion”): try to solve the problem by decomposing it in simpler (or smaller) instances • decompose and regroup (e.g., “dynamic programming”): memorize intermediate computations to avoid executing them several times 25
ICC Module Computation Lesson 2 – Computation & Algorithms II Questions ? 26
ICC Module Computation Lesson 2 – Computation & Algorithms II Binary Search: Inspection of Exam Results « Recherche dichotomique » § About 300 copies sorted by SCIPER number § How many copies do you have to look at (in the worst case) in order to find your copy? 27
ICC Module Computation Lesson 2 – Computation & Algorithms II Binary Search: Inspection of Exam Results « Recherche dichotomique » § Roughly 9 copies: 1. Split the pile into two piles of about half the size (~150 copies) 2. Check the SCIPER number of the copy on the top of the second pile: a) if it is your copy, you are done b) if it is not your copy and if your SCIPER number is larger than the one of the copy continue your search in the second pile by going to Step 1, c) otherwise continue the search in the first pile by going to Step 1 § Approx. sizes of search piles: 300, 150, 125, 63, 32, 16, 8, 4, 2, 1 28
Recommend
More recommend