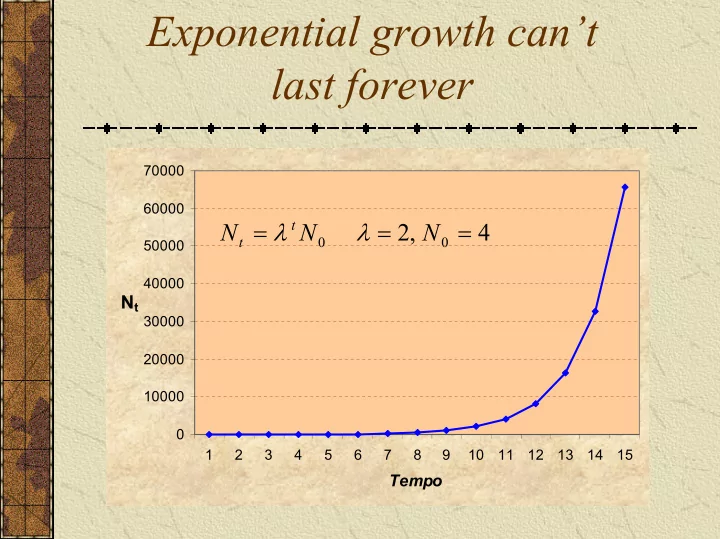
Exponential growth cant last forever 70000 60000 = = = t - PowerPoint PPT Presentation

Exponential growth can’t last forever 70000 60000 = λ λ = = t N N 2 , N 4 t 0 0 50000 40000 N t 30000 20000 10000 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Tempo

Regulation factors N t Negative feedback Density Density λ dependent independent Growth rate (birth rate, survival)

Mechanisms that may induce density dependent regulation Limited food resources: – Less consumption per capita , longer time periods searching for prey, with longer exposition to predators (affects S and b) Less space: -Smaller average territory or greater number of individuals without territory Greater predator and/or parasite pressure: -Predators “shift” to denser prey populations; greater incidence of infectious diseases. Greater use of marginal habitats of lesser quality etc. etc...

Exponential growth: constant b and d = r t N N e = − r b d constants t 0 0 0 b 0 d 0 N > ⇒ > ⇒ b d r 0 exponentia l growth 0 0 N 0 time

Density dependent regulation d = f ( N ) b 0 b = f ( N ) d 0 N > ⇒ < ⇒ b d increase b d decrease Stable equilibrium Equilibrium, N = K N=K

Carrying Capacity, K Carrying capacity ≈ Population density which is sustained by the resources available 30 K 20 N 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 tempo

How to model density-dependence 1. State the mechanisms of density dependence explicitly Example: what are the mechanisms of intra-specific competition ? 2. Assume simple analytical functions for b=f(N) and d=f(N) Etc.

Continuous breeding = − r b d 0 0 b 0 r = + d d qN d 0 t 0 t = − b b pN t 0 t N dN ( ) Substituting in = − b d N t t t dt dN [ ] we get ( ) ( ) = − − + b pN d qN N 0 t 0 t t dt dN [ ] ( ) ( ) = − − + b d p q N N 0 0 t t dt

Introducing K N K At K, dN/dt = 0 when does N t = 0 dN = Trivial equilibrium 0 ? dt dN [ ] ( ) = − + r p q N t N r t dt = N t + p q Non-trivial equilibrium K itself

The logistic equation of continuos breeders (Verhulst, 1838) r r = ∴ + = K p q + p q K Substituting here dN [ ] ( ) = − + r p q N t N t dt  −  dN N =   rN 1 dt  K  Unregulated growth Regulating factor

Growth per capita 1 dN r  −  dN N =   = − rN 1 ≡ r N dt  K  N dt K Contribution of 1 individual for population growth r r 1 dN − slope = Contrib. K N dt per capita K N

Solution of the logistic equation Solution:  −  dN N =   rN 1 KN dt K   = 0 N ( ) t + − − r t N K N e 0 0 16 12 K N 8 r=1.2 r=0.7 r=1 4 0 1 21 41 61 81 101 121 141 Tempo

Há populações com crescimento exactamente logístico ?