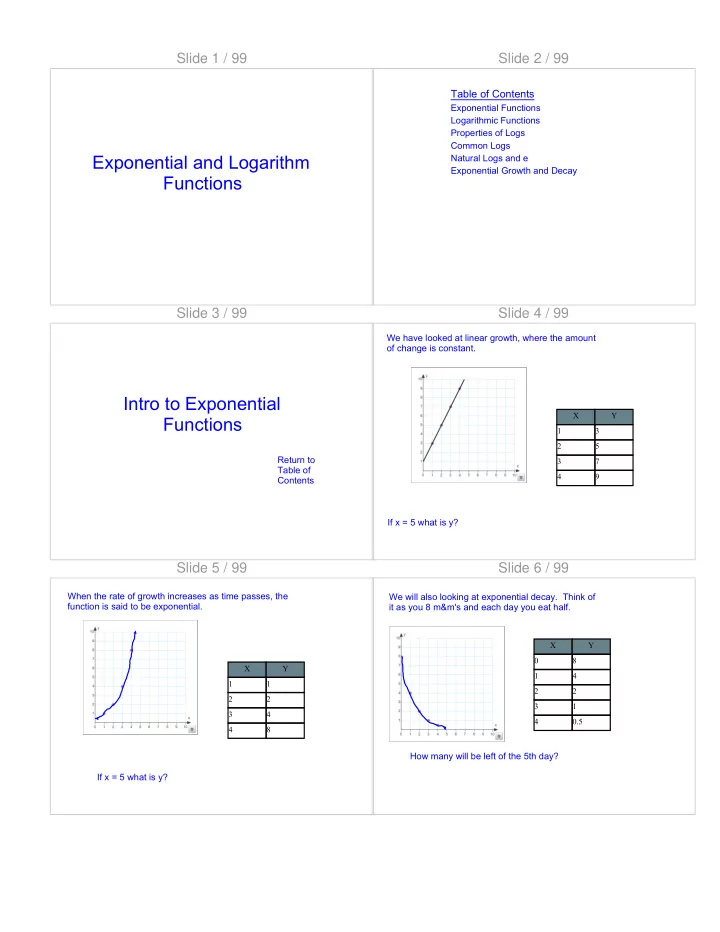

Slide 1 / 99 Slide 2 / 99 Table of Contents Exponential Functions Logarithmic Functions Properties of Logs Common Logs Exponential and Logarithm Natural Logs and e Exponential Growth and Decay Functions Slide 3 / 99 Slide 4 / 99 We have looked at linear growth, where the amount of change is constant. Intro to Exponential X Y Functions 1 3 2 5 Return to 3 7 Table of 4 9 Contents If x = 5 what is y? Slide 5 / 99 Slide 6 / 99 When the rate of growth increases as time passes, the We will also looking at exponential decay. Think of function is said to be exponential. it as you 8 m&m's and each day you eat half. X Y 0 8 X Y 1 4 1 1 2 2 2 2 3 1 3 4 4 0.5 4 8 How many will be left of the 5th day? If x = 5 what is y?
Slide 7 / 99 Slide 8 / 99 From a Graph The exponential function has a curved shape to it. For exponential growth, the function starts with the x-axis as an asymptote and increases to infinity. How can we recognize For exponential decay, the function starts at infinity an Exponential function? and decreases to the x-axis as an asymptote. Exponential Growth Exponential Decay Slide 9 / 99 Slide 10 / 99 1 Which of these are exponential growth graphs? 2 Which of these are exponential decay graphs? B C D E B C D E A A F I F I G H G H Slide 11 / 99 Slide 12 / 99 The general form of an exponential is 3 Consider the following equation is it exponential growth or decay? where x is the variable and a, b, and c are constants. A growth decay B b is the growth rate. If b > 1 then its exponential growth If 0< b < 1 then its exponential decay c is the horizontal asymptote a + c is the y-intercept
Slide 13 / 99 Slide 14 / 99 4 Considering the following equation, what is the 5 Considering the following equation, what is the equation equation of the horizontal asymptote? of the y-intercept? y=2 (0,2) A A B y=3 B (0,3) y=4 C (0,4) C y=5 D (0,5) D Slide 15 / 99 Slide 16 / 99 6 Consider the following equation is it exponential growth 7 Considering the following equation, what is the or decay? equation of the horizontal asymptote? growth A y=.2 A decay y=1 B B y=3 C D y=4 Slide 17 / 99 Slide 18 / 99 8 Considering the following equation, what is the equation 9 Consider the following equation is it exponential growth of the y-intercept? or decay? A (0,.2) A growth (0,1) decay B B C (0,3) (0,4) D
Slide 19 / 99 Slide 20 / 99 10 Considering the following equation, what is the 11 Considering the following equation, what is the equation equation of the horizontal asymptote? of the y-intercept? y=0 (0,0) A A B y=1 B (0,1) C y=3 C (0,3) D y=4 D (0,4) Slide 21 / 99 Slide 22 / 99 Graph Sketching the graph of an exponential requires using a, b, and c. 1) Identify horizontal asymptote (y = c) 2) Determine if graph is decay or growth 3) Graph y-intercept (0,a+c) 4) Sketch graph Example: Step 4 Step 1 Step 2 Step 3 growth (0,5) y = 2 Slide 23 / 99 Slide 24 / 99 Logarithm functions are the inverses of exponential functions. Exponential Log Logarithmic Functions Return to Logs have the same domain as the exponential had range, Table of that is a you cannot take the log of 0 or a negative. Contents
Slide 25 / 99 Slide 26 / 99 Rewrite the following in exponential form. Logarithms are a way to rewrite an exponential equation. Rewrite the following in logarithmic form. Slide 27 / 99 Slide 28 / 99 12 Which of the following is the correct logarithmic form of 13 Which of the following is the correct logarithmic form of ? ? A C A B B D C D Slide 29 / 99 Slide 30 / 99 14 Which of the following is the correct exponential form of 15 Which of the following is the correct exponential form of ? ? A A B B C C D D
Slide 31 / 99 Slide 32 / 99 One way to solve a log equation (or expression) is to 16 Solve convert it back exponential form. Examples: Slide 33 / 99 Slide 34 / 99 17 Solve 18 Evaluate Slide 35 / 99 Slide 36 / 99 19 Solve Properties of Logs Return to Table of Contents
Slide 37 / 99 Slide 38 / 99 Examples: Use the Properties of Logs to expand Properties of Logs These rules may seem strange but recall that logs are a way of dealing with exponents, so when we multiplied like bases we added the exponents. Just like rule 1. Slide 39 / 99 Slide 40 / 99 20 Which choice is the expanded form of the following 21 Which choice is the expanded form of the following A A B B C C D D Slide 41 / 99 Slide 42 / 99 22 Which choice is the expanded form of the following 23 Which choice is the expanded form of the following A A B B C C D D
Slide 43 / 99 Slide 44 / 99 Use and to approximate the value 24 Approximate the value of the expression given of the expression. and . Slide 45 / 99 Slide 46 / 99 25 Approximate the value of the expression given 26 Approximate the value of the expression given and . and . Slide 47 / 99 Slide 48 / 99 Examples: Use the Properties of Logs to rewrite as a single log. 27 Which choice is the contracted form of the following A B C D
Slide 49 / 99 Slide 50 / 99 28 Which choice is the contracted form of the following 29 Which choice is the contracted form of the following A A B B C C D D Slide 51 / 99 Slide 52 / 99 30 Which choice is the contracted form of the following Solving Log Equations Revisited Equations will not always be in or form. We will need to use the properties to convert them to one these forms. A B C D Slide 53 / 99 Slide 54 / 99 Extraneous answers: You can not take a log of x<0. Check to see if your solution makes the value positive. 31 Solve the following equation: r =3 works for each of the logs, but r= -1 is extraneous.
Slide 55 / 99 Slide 56 / 99 32 Solve the following equation: 33 Solve the following equation: Slide 57 / 99 Slide 58 / 99 34 Solve the following equation: Common Logs Return to Table of Contents Slide 59 / 99 Slide 60 / 99 Solving Exponential Equations Using Common Logs Common logs are logs with bases of 10. We can solve the variable as exponent using common logs Recall We can use this method to introduce common logs and then Notice the common log is written with an understood use are preferred method to find the value of the common log. base of 10. Common logs are used in the Richter Scale to Decibels. Values for common logs can be calculated from a chart or by using a scientific calculator.
Slide 61 / 99 Slide 62 / 99 35 Solve the following equation. 36 Solve the following equation. Slide 63 / 99 Slide 64 / 99 37 Solve the following equation. 38 Solve the following equation. Slide 65 / 99 Slide 66 / 99 Logarithmic functions can be rewritten as the ratio of 39 Find the approximate value of common logs. The advantage of this is that we have a method of calculating the value of common logs. Find the approximate value of
Slide 67 / 99 Slide 68 / 99 40 Find the approximate value of 41 Find the approximate value of Slide 69 / 99 Slide 70 / 99 e has a constant value of about 2.71828 e is the number used when something is continually growing, like a bacteria colony or an oil spill. The Natural Log is the inverse function of a base e function. Base e and Natural Logs Return to Table of Contents Slide 71 / 99 Slide 72 / 99 Work with e and ln the same way you did 10 and log. Write the following in the equivalent exponential or log form. For example:
Slide 73 / 99 Slide 74 / 99 Solve the following equations. Solve the following equations. Only 60.6 is a solution because ln(3(-60.6)) and ln(2(-60.6)) are undefined. Slide 75 / 99 Slide 76 / 99 The amount of money in a savings account, A, Again,using the compounded continually formula of A=Pe rt can be found using the continually compounded interest formula of If $500 is invested at 4% , how long until the account balance is doubled? A=Pe rt , where P is the principal (amount deposited), r is the annual interest rate (in decimal form), and t is time in years. If $500 is invested at 4% for 2 years, what will account balance be? It will take about 17.3 years for the money to double. $541.64 in 2 years. Slide 77 / 99 Slide 78 / 99 42 Find the value of x. 43 Find the value of x.
Slide 79 / 99 Slide 80 / 99 44 Find the value of x. 45 Find the value of x. Slide 81 / 99 Slide 82 / 99 46 Find the value of x. 47 Find the value of x. Slide 83 / 99 Slide 84 / 99 48 The amount of money in a savings account, A, can be 49 The amount of money in a savings account, A, can be found using the continually compounded interest found using the continually compounded interest formula formula of A=Pe rt , of A=Pe rt , where P is the principal (amount deposited), where P is the principal (amount deposited), r is the annual interest rate (in decimal form), r is the annual interest rate (in decimal form), and t is time in years. and t is time in years. If $1000 is invested at 4% for 3 years,what is the If $1000 is invested at 4%, how long until the account account balance? balance is doubled? HINT HINT
Recommend
More recommend