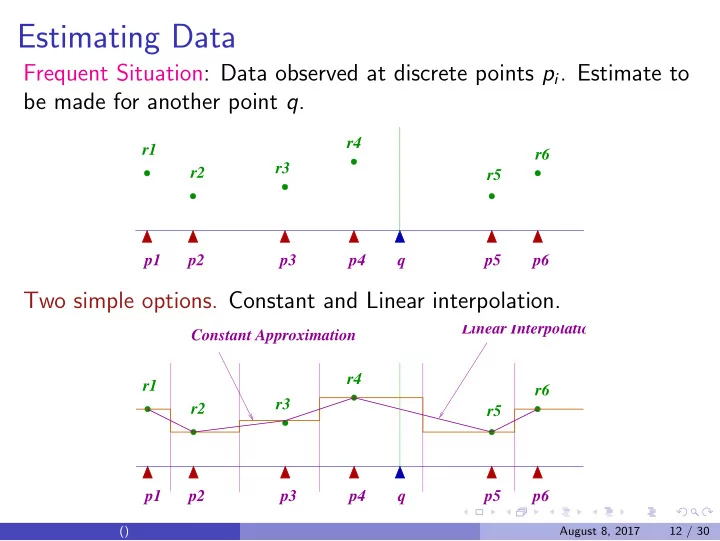
Estimating Data Frequent Situation: Data observed at discrete points - PowerPoint PPT Presentation

Estimating Data Frequent Situation: Data observed at discrete points p i . Estimate to be made for another point q . r4 r1 r6 r3 r2 r5 p1 p2 p3 p4 q p5 p6 Two simple options. Constant and Linear interpolation. Linear Interpolation Constant Approximation r4 r1 r6 r3 r2 r5 p1 p2 p3 p4 q p5 p6 () August 8, 2017 12 / 30

MyWatershed -estimating total rainfall MyWatershed Shown here is my watershed with the Rain−gauges locations of rain-gauges. Estimate the total rainfall over my watershed ( in cubic-meters . Question: What should I assume as the rainfall at point p ? Heuristic: Assign to each point p , the rainfall at the closest gauge. () August 8, 2017 13 / 30

The Voronoi perpendicular a bisector c d b region(c) : All points for which c is the closest. Note that it depends on the presence of other points. () August 8, 2017 14 / 30

The Domain decomposition () August 8, 2017 15 / 30

MyWatershed -the overlay MyWatershed Draw your watershed on a graph-paper. Let g ( i ) be a gauge and let the reading at g ( i ) be r ( i ). A(i) We want to find all points p for g(i) which the closest point is g ( i ). () August 8, 2017 16 / 30

MyWatershed -the overlay MyWatershed Draw your watershed on a graph-paper. Let g ( i ) be a gauge and let the reading at g ( i ) be r ( i ). A(i) We want to find all points p for g(i) which the closest point is g ( i ). Compute the polygon P ( i ) by the method of bisectors. Let A ( i ) be the fraction of the area lying inside my waterhsed. () August 8, 2017 16 / 30

MyWatershed -the construction MyWatershed Measure A ( i ) using the graph paper. Ignore area outside the watershed. The sum � i A ( i ) = A the total A(i) area of the watershed. g(i) Average rainfall Ignore � A ( i ) r ( i ) r = � A ( i ) Finally... Total Volumne= A . r () August 8, 2017 17 / 30

Domain Decomposition Division of the domain into non-overlapping triangles () August 8, 2017 18 / 30

Internal Section Formula a x 1−x c q p 1−y r y b f ( p ) = (1 − x ) · f ( a ) + x · ( y · f ( c ) + (1 − y ) · f ( b )) () August 8, 2017 19 / 30

Delaunay-Voronai Dual Decomposition () August 8, 2017 20 / 30

Other Options MyWatershed a,f(a) A(i) g(i) x,f(x) c,f(c) b,f(b) x=u1.a+u2.b+u3.c u1+u2+u3=1 f(x)=u1.f(a)+u2.f(b)+u3.f(c) () August 8, 2017 21 / 30

Measuring Stream-flows V-notch weir. Suitable for small streams. A V-notch is inserted in the stream so that there is sufficient head behind the V-notch. Measurements are taken on the height of the For a 90-degree stream-level on the V -notch: Q = 2 . 5 H 5 / 2 where V-notch. Q in cu.ft/s, and H is ht. of Flow: cu.m./s is given head above crest. Example: by an empirical If H = 0 . 25 ft then relationship. Q = 0 . 078 cu.ft/s. () August 8, 2017 22 / 30

Measuring Stream-flows For larger streams Use a stick-mounted flow-meter. Select a stream cross-section. Follow a schedule of measurements at various depths and points on the cross-section. Use formula to compute flow. () August 8, 2017 23 / 30

Measuring Stream-flows () August 8, 2017 24 / 30

Flow in Open-Channel Mannings Eqn. Example (Fetter) : An aquaduct is with a slope of V = (1 . 49 R 2 / 3 S 1 / 2 ) / n 5ft/mile and with a rectangular cross-section of where 50ft and water depth of 8ft. V is average velocity in ft/s What is the average velocity? R is surface-area/wet-perimeter in ft. S is the slope of the water R = (50 × 8) / 66 = 6 . 06. and n is as below: S = 5 / (1760 × 3) = 0 . 000947. Mountain streams 0.04 n = 0 . 02. winding stream 0.035 natural streams 0.025 V = 3 . 048 ft / s unlined canals 0.02 smooth concrete 0.012 () August 8, 2017 25 / 30

Another Problem Mumbai needs 3000 mega-liters/day which come from lakes about 100 km away and about 500 ft above Mumbai in elevation. Estimate the the number of pipes needed to transfer this water, if the diameter of these pipes is 2m. Estimate the total flow and the height of water in the nalla opposite Hostel 5 on a rainy day. () August 8, 2017 26 / 30

Diversion Based Irrigation Small bandaharas within stream and small canals to take away water. Few gates and flood based canal delivery. extraction through wells () August 8, 2017 27 / 30

Diversion Based Irrigation-A Section () August 8, 2017 28 / 30

Measuring other flows Infiltration: Standard models. Also Infiltrometer which measures infiltration and conductivity, a hydrogeological term. ◮ slope, soil properties, vegetation. Transpiration: Standard data from experimental plots. Also FAO and agriculture department. ◮ Typically depends on wind velocity, air temperature, humidity and also plant properties. ◮ Typically about 100 to 200 times of wieght gained by plant. For crops, about 3mm per day. Evaporation. From soil as well as water bodies. 1mm-5mm per day. Depends on air temperature, humidity and velocity. Seepage, Groundwater flows: Depends on conductivity and hydraulic heads . Darcy’s law. () August 8, 2017 29 / 30

Thanks () August 8, 2017 30 / 30

Water and Development Part 2c: Sub-surface and Groundwater Milind Sohoni www.cse.iitb.ac.in/ ∼ sohoni email: sohoni@cse.iitb.ac.in () August 10, 2017 1 / 26

Objectives Sub-surface and Groundwater: Stocks and Flows. How does GW and SSW function as stocks? Sub-surface water (a.k.a. Soil Moisture) in the top few meters. Groundwater: deeper, saturated. Complex interaction between SSW and GW. What are the basic mechanisms (laws and models) by which they work? What are the key parameters to describe these and how are these measured? () August 10, 2017 2 / 26

Groundwater Deep. Accessed through wells and bore-wells. Water-Table: important concept. How much water is available through-out the year? Specific Yield Does it depend on the nature of soil/rock underneath? Aquifer How do different wells interact? Conductivity Well Ground ��� ��� ��� ��� ��� ��� WaterTable ��� ��� ��� ��� () August 10, 2017 3 / 26

Porosity: Soil as a container Porosity: The fraction of empty space with a soil. em Depends on configuration. Porosity depends on the regularity of particle High Porosity Low size. Sand 0.1mm-1mm The more sorted the Silt 0.005mm-0.1mm particles, the higher the Clay < 0.005mm porosity. May change across different areas and different depths. () August 10, 2017 4 / 26

Moisture Moisture: The volume fraction of wet soil which is water. Water exists in within the voids and is either (i) loosely depth held, or (ii) tightly held by soil particles. Soil moisture n increases with depth and reaches its theoretical maximum of saturation proposity p . This is called saturation. At this point, soil moisture equals porosity. p moisture () August 10, 2017 5 / 26

Saturation The region below is called the saturated region. The region above is the unsaturated region. This depth is called the depth of the water-table . At this depth, water appears spontaneously in a dug-well. Saturated water can be extracted easily. Unsaturated region: important for plants and microbes. Groundwater also flows just as ordinary water, albeit at different rates. Groundwater flows eventually go to streams, rivers and oceans. Well Ground ��� ��� ��� ��� ��� ��� WaterTable ��� ��� ��� ��� () August 10, 2017 6 / 26

Moisture when it rains: When the rain falls (a) Before Rains: surface moisture less than porosity. (b) Start of Rain: surface mosture starts increasing: Infiltration phase. (c) Saturation: Surface saturates: Run-Off phase. (d) Rain Stops: Moisture descends and joins water-table by gravity. Depth Water−Table (b) (d) (a) (c) () August 10, 2017 7 / 26

Porosity and Soil Moisture Key Quantites Soil Moisture: Fraction of soil-volume filled with water. Porosity of a soil: Maximum possible value of soil moisture. Take a fixed volume V sample of soil. ◮ Use a standard gouge, scoop, screw or core. Let W s be its weight. Let W d be the weight of the sample after oven-drying. Let W w be the weight of the sample after immersing it in water till it gets saturated. Let ρ be the density of water. Porosity p = W w − W d ρ V Moisture n = W s − W d ρ V () August 10, 2017 8 / 26