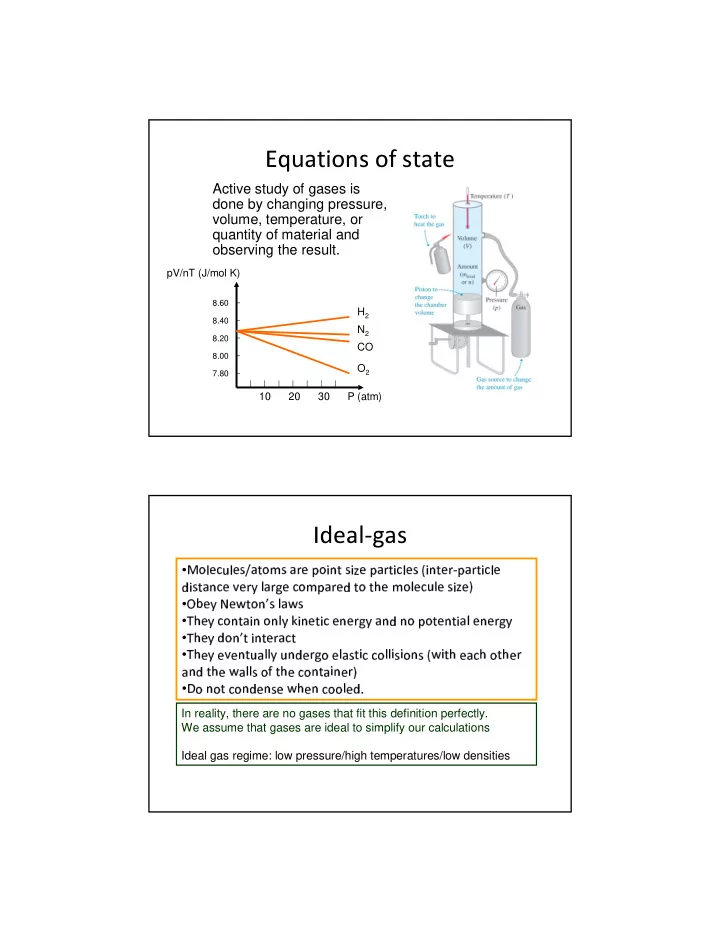
Equations of state Active study of gases is done by changing - PDF document

Equations of state Active study of gases is done by changing pressure, volume, temperature, or quantity of material and observing the result. pV/nT (J/mol K) 8.60 H 2 8.40 N 2 8.20 CO 8.00 O 2 7.80 10 20 30 P (atm) Ideal-gas � ✁ ✂ ✄ ☎ ✆ ✂ ✄ ✝ ✞ ✟ ✠ ✁ ✡ ✝ ✟ ☛ ✄ ☞ ✁ ✌ ✍ ✠ ✝ ✌ ✎ ✄ ☞ ✟ ☛ ✠ ✌ ☎ ✂ ✄ ✝ ✏ ✌ ✍ ✠ ✄ ☛ ✑ ☞ ✟ ☛ ✠ ✌ ☎ ✂ ✄ • ✒ ✌ ✝ ✠ ✟ ✍ ☎ ✄ ✓ ✄ ☛ ✔ ✂ ✟ ☛ ✕ ✄ ☎ ✁ ✡ ☞ ✟ ☛ ✄ ✒ ✠ ✁ ✠ ✖ ✄ ✡ ✁ ✂ ✄ ☎ ✆ ✂ ✄ ✝ ✌ ✎ ✄ ✗ ✄ ✔ ✚ ✄ ✛ ✠ ✁ ✍ ✜ ✝ ✂ ✟ ✛ ✝ • ✘ ✙ ✒ ✖ ✄ ✔ ☎ ✁ ✍ ✠ ✟ ✌ ✍ ✁ ✍ ✂ ✔ ✣ ✌ ✍ ✄ ✠ ✌ ☎ ✄ ✍ ✄ ☛ ✕ ✔ ✟ ✍ ✍ ✁ ☞ ✁ ✠ ✄ ✍ ✠ ✌ ✟ ✂ ✄ ✍ ✄ ☛ ✕ ✔ • ✢ ✖ ✄ ✔ ✒ ✁ ✍ ✜ ✠ ✌ ✍ ✠ ✄ ☛ ✟ ☎ ✠ • ✢ ✒ ✖ ✄ ✔ ✄ ✓ ✄ ✍ ✠ ✆ ✟ ✂ ✂ ✔ ✆ ✍ ✄ ☛ ✕ ✁ ✄ ✂ ✟ ✝ ✠ ✌ ☎ ☎ ✁ ✂ ✂ ✌ ✝ ✌ ✁ ✍ ✝ ✏ ✛ ✌ ✠ ✖ ✄ ✟ ☎ ✖ ✁ ✠ ✖ ✄ ☛ • ✢ ✒ ✟ ✍ ✠ ✖ ✄ ✛ ✟ ✂ ✂ ✝ ✁ ✤ ✠ ✖ ✄ ☎ ✁ ✍ ✠ ✟ ✌ ✍ ✄ ☛ ✗ ✁ ✍ ✁ ✠ ☎ ✁ ✍ ✒ ✄ ✍ ✝ ✄ ✛ ✖ ✄ ✍ ☎ ✁ ✁ ✂ ✄ ✒ ✦ • ✥ In reality, there are no gases that fit this definition perfectly. We assume that gases are ideal to simplify our calculations Ideal gas regime: low pressure/high temperatures/low densities

Ideal-gas equation � ✁ ✂ ✄ ☎ ✆ ✆ ✝ ✄ ☎ ✞ pV = nRT ✁ ✟ ✠ ✡ ✝ ☛ ☎ ☞ ✁ ✌ ✝ ☛ ✍ ☎ ✄ ✠ ✎ ☛ ✠ ✡ ☎ ✆ ✏ ✁ ✑ ☎ ☛ ✂ ☎ ✄ ✒ ✑ ✝ ✄ ☎ ✓ ✁ ✔ ✕ ☎ ✒ ✡ ✖ ✒ ✆ ✗ ✠ ✌ ✆ ✑ ✒ ✌ ✑ ✘ ✙ ✚ ✛ ✜ ✢ ✣ ✤ ☛ ✠ ✡ ✥ m total = nM ✧ ✆ ✔ ✌ ✖ ✑ ★ ☎ ✔ ✕ ☎ ✌ ✑ ✔ ✑ ✩ ✁ ☛ ✠ ✡ ✒ ✄ ☛ ✒ ✆ ✆ ✦ m pV = RT total ✪ ☎ ✠ ✍ ✑ ✒ ✔ ✌ M ρ = m total / V ✧ ρ ✆ ✔ ✌ ✖ ✑ ★ ☎ ✔ ✕ ☎ ✌ ✑ ✔ ✑ ✩ ✁ ✕ ☎ ✌ ✆ ✔ ✑ ✩ pM ✪ ρ = ☎ ✠ ✍ ✑ ✒ ✔ ✌ RT ✫ ✠ ✑ ✔ ✗ ☎ ✌ ✠ ✑ ✒ ✑ ✔ ✠ ✌ ✚ ✡ ✠ ✬ ☎ ✄ ✗ ✒ ✆ ☎ ✁ ✔ ✌ ✑ ☎ ✌ ✆ ✔ ✟ ☎ ✭ ✝ ✂ ✂ ☎ ✄ ✗ ✒ ✆ ☎ ✁ ☎ ✮ ✑ ☎ ✌ ✆ ✔ ✟ ☎ ✯ ✝ ✒ ✌ ✑ ✔ ✑ ✔ ☎ ✆ Ideal-gas equation � ✁ ✂ ✄ ☎ ✆ ✆ ✝ ✄ ☎ ✞ pV = nRT ✁ ✟ ✠ ✡ ✝ ☛ ☎ ☞ ✁ ✌ ✝ ☛ ✍ ☎ ✄ ✠ ✎ ☛ ✠ ✡ ☎ ✆ ✏ ✁ ✑ ☎ ☛ ✂ ☎ ✄ ✒ ✑ ✝ ✄ ☎ ✓ ✁ ✔ ✕ ☎ ✒ ✡ ✖ ✒ ✆ ✗ ✠ ✌ ✆ ✑ ✒ ✌ ✑ ✘ ✙ ✚ ✛ ✜ ✢ ✣ ✤ ☛ ✠ ✡ ✥ N = nN ✁ ✲ ✟ ✠ ✖ ✄ ✒ ✕ ✄ ✠ ✌ ✝ ☛ ✍ ☎ ✄ ✧ ✆ ✔ ✌ ✖ ✑ ★ ☎ ✔ ✕ ☎ ✌ ✑ ✔ ✑ ✩ A ✰ ✱ R = = pV N T NkT ✪ ☎ ✠ ✍ ✑ ✒ ✔ ✌ N A The constant term R / N A is referred to as Boltzmann's constant, in honor of the Austrian physicist Ludwig Boltzmann (1844–1906), and is represented by the symbol k :

Ideal-gas equation (contd.) p V p V � ✠ ✄ ✗ ✠ ✌ ✆ ✑ ✒ ✌ ✑ ☛ ✒ ✆ ✆ ✁ ✬ ☎ ✠ ✍ ✑ ✒ ✔ ✌ = 1 1 2 2 T T 1 2 pV = const � Boyle’s law . ✠ ✄ ✗ ✠ ✌ ✆ ✑ ✒ ✌ ✑ ✑ ☎ ☛ ✂ ☎ ✄ ✒ ✑ ✝ ✄ ☎ ✁ ✬ ☎ ✠ ✍ ✑ ✒ ✔ ✌ ✂ ✄ ☎ ✆ ✝ ✞ ✟ ✠ ✄ CPS question A quantity of an ideal gas is contained in a balloon. Initially the gas temperature is 27°C. You double the pressure on the balloon and change the temperature so that the balloon shrinks to one-quarter of its original volume. What is the new temperature of the gas? A. 54°C B. 27°C C. 13.5°C D. –123°C E. –198°C

CPS question p This pV –diagram shows three possible states of a certain amount 3 of an ideal gas. Which state is at the highest 2 temperature? 1 A. state #1 V B. state #2 O C. state #3 D. Two of these are tied for highest temperature. E. All three of these are at the same temperature. Summary:Equations of state pV = nRT � ✁ ✂ ✄ ☎ ✆ ✆ ✝ ✄ ☎ ✞ ✁ ✟ ✠ ✡ ✝ ☛ ☎ ☞ ✁ ✌ ✝ ☛ ✍ ☎ ✄ ✠ ✎ ☛ ✠ ✡ ☎ ✆ ✏ ✁ ✑ ☎ ☛ ✂ ☎ ✄ ✒ ✑ ✝ ✄ ☎ ✓ ✁ ✔ ✕ ☎ ✒ ✡ ✖ ✒ ✆ ✗ ✠ ✌ ✆ ✑ ✒ ✌ ✑ ✘ ✙ ✚ ✛ ✜ ✢ ✣ ✤ ☛ ✠ ✡ ✥ pV = NkT k: Boltzmann’s constant ; k = R/N A =1.38x10 -23 J/K

Kinetic theory of an ideal gas Pressure of a gas The pressure that a gas exerts is caused by the impact of its molecules on the walls of the container. Consider a cubic container of volume V containing N molecules with a speed v

Consider a gas molecule colliding elastically with the right wall of the container and rebounding from it. The force on the wall is obtained using Newton’s second law as follows , ∆ P = F ∆ P : change in momentum , ∆ t And the pressure: ∆ P 1 1 = = P F , ∆ A A t Total change in momentum ∆ P of all the molecules during a time interval ∆ t = Change in momentum of one molecule, times the number of molecules that hit the wall during the interval ∆ t : Change in momentum of one molecule: ∆ p = mv − − mv = mv ( ) 2 x x x Change in momentum of all the molecules: ∆ = × P mv N ( 2 ) x hit N N 1 = ∆ ∆ = ∆ N v tA P mv tA 2 � hit x x V V 2 Finally, the pressure is given by: ∆ P N 1 = = P mv 2 x ∆ A t V

2 by ( v x Particles move in random directions, so we replace v x 2 ) av N = P m v 2 ( ) x av V or, equivalently 1 = PV N mv 2 2 ( ) x av 2 Molecular interpretation of temperature 1 = = PV NkT N mv 2 2 ( ) x av 2 or 1 1 = mv kT 2 ( ) x av 2 2 There is nothing special about the x direction, in general: = = v v v 2 2 2 ( ) ( ) ( ) x av y av z av = + + = v v v v v 2 2 2 2 2 and ( ) ( ) ( ) ( ) 3 ( ) av x av y av z av x av Therefore: The average kinetic energy of a molecule is: 1 3 = = E mv kT 2 ( ) Kin av 2 2 The absolute temperature is a measure of the average translational kinetic energy of the molecules

CPS question An ideal gas is trapped in a chamber, inside a thermally insulated container (see figure). When the partition is broken or removed, the gas expands and fills the entire volume of the container. As a result, the final temperature of the gas after the expansion is: A. Lower than the initial temperature B. Higher than the initial temperature C. The temperature remains constant Equipartition theorem 1 3 = = E mv kT 2 ( ) Kin av 2 2 When a substance is in equilibrium, there is an average energy of 1/2 kT per molecule, or 1/2RT per mole, associated with each degree of freedom z y x

Molar heat capacity Kinetic energy per mole: 3 = E Kin RT 2 dQ = dE Kin 3 = C V dT RdT � 2 3 = C V R ✁ 2 3 = = C ( 8 . 314 J/mol.K ) 12 . 47 J/mol.K ✂ V 2 Molar heat capacity Kinetic energy per mole: 3 = E Kin RT 2 dQ = dE Kin 3 = C V dT RdT � 2 3 = C V R ✁ 2 3 = = C ( 8 . 314 J/mol.K ) 12 . 47 J/mol.K ✂ V 2 Works well for monoatomic gases… what’s wrong with the others…?

Heat absorption into degrees of freedom A molecule can absorb energy in translation, and also in rotation and vibrations in its structure CPS question The molar heat capacity at constant volume of diatomic hydrogen gas (H 2 ) is 5 R /2 at 500 K but only 3 R /2 at 50 K. Why is this? A. At 500 K the molecules can vibrate, while at 50 K they cannot. B. At 500 K the molecules cannot vibrate, while at 50 K they can. C. At 500 K the molecules can rotate, while at 50 K they cannot. D. At 500 K the molecules can rotate, while at 50 K they cannot.

Heat capacity of solids Solids can absorb energy in the vibrational modes. A 3-dimensional solid has 3 vibrational degrees of freedom+3 translational… = C V R � 3 ✁ C = = 3 ( 8 . 314 J/mol.K ) 24 . 9 J/mol.K V Dulong and Petit’s law (Valid at high temperature due to quantum nature of the vibrations) ✂ ✄ ☎ ✆ ✝ ✞ ✞ ✟ ✠ ✡ ✞ ☛ ☞ ✌ ✄ ✍ ✎ ✏ ✑ ☛ ✒ ✏ ✓ ✔ ☛ ✏ ✡ ✍ ✡ ✕ ✖ ✝ ✞ ✡ ✗ ✏ ☛ ✏ ✝ ✑ kT RT 2 2 = = v m M mp The fraction of molecules dN with speeds between v and v+dv is given by = dn f v dv ( ) The average speeds are given by: kT ∞ 8 v ave = vf v dv = ( ) ∫ π m 0 kT ∞ 3 = = v ave v f v dv 2 2 ( ) ∫ m 0