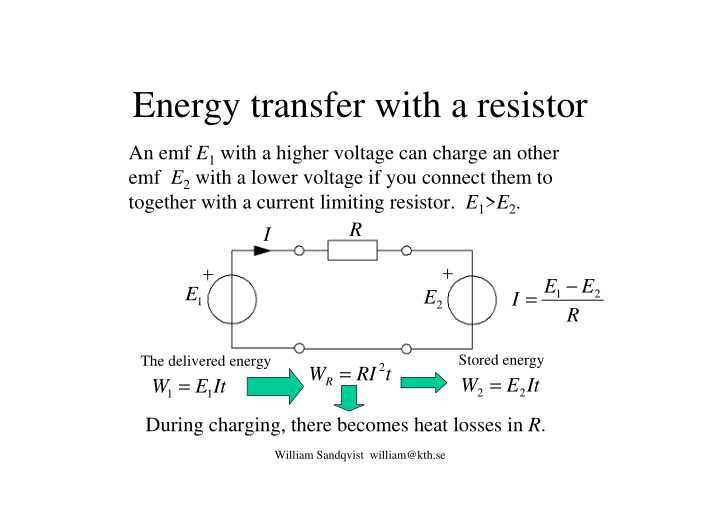



Energy transfer with a resistor An emf E 1 with a higher voltage can charge an other emf E 2 with a lower voltage if you connect them to together with a current limiting resistor. E 1 > E 2 . R I 1 − E E E E = I 2 1 2 R Stored energy The delivered energy = W R RI t 2 2 = 1 = W E It W E It 2 1 During charging, there becomes heat losses in R . William Sandqvist william@kth.se
Energy transfer with an inductor E > E E < E 1 2 1 2 L E E 2 1 With an inductor one can transfer energy from a larger emf to a smaller, E 1 > E 2 , Step Down , but also from a smaller emf to a larger, E 1 < E 2 , Step Up . This in theory is completely without losses. William Sandqvist william@kth.se
Step Up L E < E 1 2 E E 1 2 Pulse width modulation • Transistor • PWM-unit • Diode Transistor and diode acts together as a switch controlled by the PWM unit. William Sandqvist william@kth.se
E < E Step Up 1 2 i L L E E E E 2 2 1 1 i t t on off t = D on • DutyCycle D : + t t on off William Sandqvist william@kth.se
The coil current inertia = t 0 di di E i = ⇔ = E L L Ψ dt dt L i E Pump E Waterwheel L Flywheel t The inductor has current-inertia . The current can not change immediately. A fluid analogy: The inductor is a water mill with a flywheel. William Sandqvist william@kth.se
Energy transfer with an inductor L Let E 1 drive an increasing E E current through L during i 2 1 on t on . The current then reaches I max . i I max I i avg E 1 on I 0 L t t on William Sandqvist william@kth.se
Energy transfer with an inductor i switch the inductor so that L off L now continnues the current through E 2 . E 2 > E 1 E E 2 1 means that the current will be decreasing. It will reach I 0 again after time t off . i 1 − E E I The times t on , t off i 2 max off L I are those that avg gives us a I 0 stationary plot. t t off William Sandqvist william@kth.se
Energy transfer with an inductor i E 1 1 − E E i I L 2 off max L I i avg on I Stationary 0 t t t Energy: off on = ⋅ ⋅ = − ⋅ ⋅ = W E I t W E E I t W W ( ) on 1 avg on off 1 2 avg off on off + E t t 1 1 = = = ⋅ E E 2 on off − − E t D 2 1 D 1 1 1 off William Sandqvist william@kth.se
5V → 50V ? L E E 50V 2 1 5V E 1 5 = ⋅ � = − = − = E E D 1 1 1 90 % − 2 1 D E 1 50 2 William Sandqvist william@kth.se
Resistiv load? L C 5V 50V The current to the load will flow intermittently only during t off , so the voltage needs to be smoothed with a capacitor C . William Sandqvist william@kth.se
( What is a diode? ) A K ideal diode Semiconductor diode Symbol and characteristic conduction direction blocking direction Fluid Analogy check valve William Sandqvist william@kth.se
C ( What is a transistor? ) B Fluid analogy E The classic bipolar transistor, is earlier development than the MOS transistor. A small "base current" I B can control up to 100 times ( h FE ) bigger ”collector current” I C . I = h C FE PIC I B ≈ h 100 FE > � = I I 1 mA 100 mA B C William Sandqvist william@kth.se
Practical dimensioning? It is simple to set up the Step-up converter's output voltage with the DutyCycle D ! This we do at the lab. In practice it is much more difficult . An electronics engineer is faced with many questions: At what current "saturate" the coil iron core? How big internal resistance has the inductor? How big are the load variations? What values to L and C and f should be choosen? It is common to simulate the circuit with more realistic component models than what we use here. LT:s App note has the title ” Switching Regulators for Poets ” William Sandqvist william@kth.se
A problem is that while everyone agrees that working switching regulators are a good thing, everyone also agrees that they are difficult to get working. Unfortunately, switching regulators are one of the most difficult linear circuits to design. Mysterious modes, sudden, seemingly inexplicable failures, peculiar regulation characteristics and just plain explosions are common occurrences. Diodes conduct the wrong way. Things get hot that shouldn’t. Capacitors act like resistors, fuses don’t blow and transistors do. The output is at ground, and the ground terminal shows volts of noise. … Jim Williams William Sandqvist william@kth.se
Jim Williams at lab William Sandqvist william@kth.se
Simulation D = 86 % Startup Sequence 0…1ms 1 = E 5 Simulation with an ideal switch The voltage is stepping upwards… William Sandqvist william@kth.se
Simulation 2 ≈ E 30 Stationary at 100 ms E 1 = 5V E 2 ≈ 30V D = 86% 1 = E 5 William Sandqvist william@kth.se
William Sandqvist william@kth.se
Recommend
More recommend