Electron beam results Jerry Gilfoyle The Configurations of CO - PowerPoint PPT Presentation

More On Carbon Monoxide ∆ E = 0 . 25 ± 0 . 05 eV − → Electron beam results Jerry Gilfoyle The Configurations of CO 1 / 28

More On Carbon Monoxide ∆ E = 0 . 25 ± 0 . 05 eV − → Electron beam results Jerry Gilfoyle The Configurations of CO 1 / 28

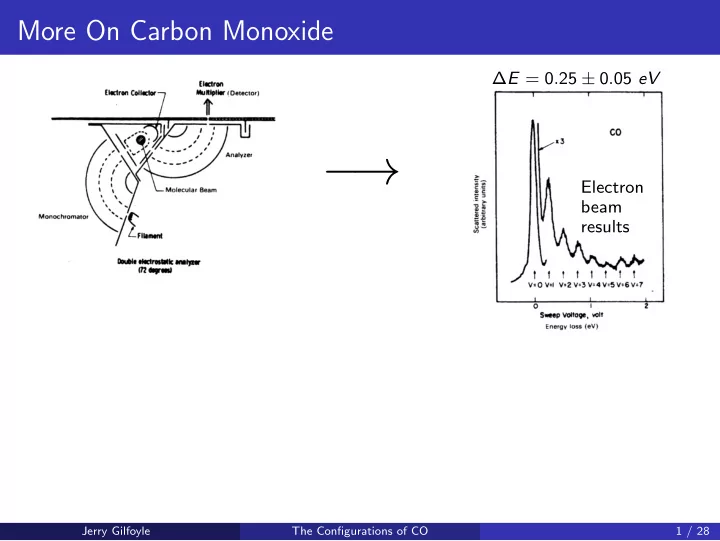
More On Carbon Monoxide ∆ E = 0 . 25 ± 0 . 05 eV − → Electron beam results − → Jerry Gilfoyle The Configurations of CO 1 / 28

Even More On Carbon Monoxide CO Absorption Spectrum → Electron beam Incident light results ∆ E = 0 . 25 ± 0 . 05 eV Photon detector CO gas target Jerry Gilfoyle The Configurations of CO 2 / 28

Even More On Carbon Monoxide CO Absorption Spectrum → Electron beam Incident light results ∆ E = 0 . 25 ± 0 . 05 eV Photon detector CO gas target Carbon−Monoxide Spectrum Absorption 0.2550 0.2600 0.2650 0.2700 0.2750 Energy (eV) Jerry Gilfoyle The Configurations of CO 2 / 28

Is Carbon Monoxide A Rigid Rotator? Excited states of carbon monoxide (CO) can be observed by measuring the absorption spectrum shown below. The molecule can both vibrate and rotate at the same time. The rotational energy states of a rigid rotator are E ℓ = � 2 2 I ℓ ( ℓ + 1) where I is the moment of inertia. The vibrational part of the energy is described by the harmonic oscillator so E n = ( n + 1 2 ) � ω 0 with ∆ E = � ω 0 = 0 . 25 ± 0 . 05 eV from our previous results. How do you get the expression above for the rotational energy? Is CO a rigid rotator? Carbon−Monoxide Spectrum Absorption 0.2550 0.2600 0.2650 0.2700 0.2750 Energy (eV) Jerry Gilfoyle The Configurations of CO 3 / 28

Is Carbon Monoxide A Rigid Rotator? Excited states of carbon monoxide (CO) can be observed by measuring the absorption spectrum shown below. The molecule can both vibrate and rotate at the same time. The rotational energy states of a rigid rotator are E ℓ = � 2 2 I ℓ ( ℓ + 1) where I is the moment of inertia. The vibrational part of the energy is described by the harmonic oscillator so E n = ( n + 1 2 ) � ω 0 with ∆ E = � ω 0 = 0 . 25 ± 0 . 05 eV from our previous results. How do you get the expression above for the rotational energy? Is CO a rigid rotator? Carbon−Monoxide Spectrum Absorption 0.2550 0.2600 0.2650 0.2700 0.2750 Energy (eV) Jerry Gilfoyle The Configurations of CO 3 / 28

The Plan 1 What is the kinetic and potential energy between the carbon and oxygen atoms in CO in the CM frame in cartesian and spherical coordinates? 2 How do you decompose the kinetic energy into radial and angular parts? 3 What is the Schroedinger equation for the rigid rotator? 4 What is the solution of the rigid rotator Schroedinger equation? Jerry Gilfoyle The Configurations of CO 4 / 28

Coordinates y r=r − r 1 2 r 1 R x r 2 Jerry Gilfoyle The Configurations of CO 5 / 28

Coordinates y y m 1 r=r − r r=r − r 1 1 2 2 r 1 r 1 R R cm x x m r 2 r 2 2 Jerry Gilfoyle The Configurations of CO 5 / 28

Angular Momentum µ α Jerry Gilfoyle The Configurations of CO 6 / 28

Angular Momentum y p α p p Τ r µ r x µ α Jerry Gilfoyle The Configurations of CO 6 / 28

Going To 3D The Laplacian � 1 ∂ 2 � � � � � ∂ r 2 ∂ 1 ∂ sin θ ∂ 1 ∇ 2 ψ = + + ψ r 2 sin θ r 2 sin 2 θ r 2 ∂φ 2 ∂ r ∂ r ∂θ ∂θ Jerry Gilfoyle The Configurations of CO 7 / 28

Going To 3D The Laplacian � 1 ∂ 2 � � � � � ∂ r 2 ∂ 1 ∂ sin θ ∂ 1 ∇ 2 ψ = + + ψ r 2 sin θ r 2 sin 2 θ r 2 ∂φ 2 ∂ r ∂ r ∂θ ∂θ The Schroedinger Equation in 3D − � 2 2 µ ∇ 2 ψ + V ( r ) ψ = E ψ � 1 − � 2 ∂ 2 ∂ � r 2 ∂ � 1 ∂ � sin θ ∂ � 1 � + + ψ r 2 sin θ r 2 sin 2 θ r 2 ∂φ 2 2 µ ∂ r ∂ r ∂θ ∂θ + V ( r ) ψ = E ψ Jerry Gilfoyle The Configurations of CO 7 / 28

Going To 3D Steps along the way. m 2 − 1 � sin θ d Θ � d ℓ + sin 2 θ Θ = A Θ sin θ d θ d θ Jerry Gilfoyle The Configurations of CO 8 / 28

Going To 3D Steps along the way. m 2 − 1 � sin θ d Θ � d ℓ + sin 2 θ Θ = A Θ sin θ d θ d θ Legendre’s Associated Equation (1 − z 2 ) d 2 Θ m 2 dz 2 − 2 z d Θ � � ℓ dz + A − Θ = 0 w here z = cos θ 1 − z 2 Jerry Gilfoyle The Configurations of CO 8 / 28

Going To 3D Steps along the way. m 2 − 1 � sin θ d Θ � d ℓ + sin 2 θ Θ = A Θ sin θ d θ d θ Legendre’s Associated Equation (1 − z 2 ) d 2 Θ m 2 dz 2 − 2 z d Θ � � ℓ dz + A − Θ = 0 w here z = cos θ 1 − z 2 And its recursion relationship when m ℓ = 0 a k +2 = k ( k + 1) − A ( k + 2)( k + 1) a k Jerry Gilfoyle The Configurations of CO 8 / 28

Going To 3D We have the recursion relationship when m ℓ = 0 a k +2 = k ( k + 1) − A ( k + 2)( k + 1) a k Notice. Given a 0 → a 2 → a 4 · · · and given a 1 → a 3 → a 5 · · · so ∞ ∞ ∞ a k z k = a k z k + � � � a k z k Θ( z ) = even k =0 odd and we choose a 0 = a 1 = 1. Jerry Gilfoyle The Configurations of CO 9 / 28

ξ Recall the Harmonic Oscillator Solution β 2 = m ω 0 / � ξ = β x log ( f ( ξ )) 2 ( ξ ) Red Dashed - ⅇ - ξ 2 H 50 Green Dashed - offset × ⅇ ξ 2 Jerry Gilfoyle The Configurations of CO 10 / 28

Another Convergence Problem Truncated Calculation of Θ ( z = 1 ) , m l = 0 2.5 2.0 Θ ( z ) 1.5 Θ( z = 1) = � k max k =0 a k (1) k 1.0 k ( k +1) − A a k +2 = ( k +2)( k +1) a k 0.5 0.0 0 20 40 60 80 100 k max Jerry Gilfoyle The Configurations of CO 11 / 28

Another Convergence Problem Truncated Calculation of Θ ( z = 1 ) , m l = 0 3.5 3.0 2.5 Θ ( z ) 2.0 Θ( z = 1) = � k max k =0 a k (1) k 1.5 k ( k +1) − A a k +2 = ( k +2)( k +1) a k 1.0 0.5 0.0 0 200 400 600 800 1000 k max Jerry Gilfoyle The Configurations of CO 12 / 28

Another Convergence Problem Truncated Calculation of Θ ( z = 1 ) , m l = 0 5 4 3 Θ ( z ) Θ( z = 1) = � k max k =0 a k (1) k 2 k ( k +1) − A a k +2 = ( k +2)( k +1) a k 1 0 0 2000 4000 6000 8000 10000 k max Jerry Gilfoyle The Configurations of CO 13 / 28

Another Convergence Problem Truncated Calculation of Θ ( z = 1 ) , m l = 0 5 4 Θ( z = 1) = � k max k =0 a k (1) k 3 Θ ( z ) k ( k +1) − A a k +2 = 2 ( k +2)( k +1) a k 1 Blue - Truncated Calculation of Θ ( z = 1 ) , m l = 0 Green - ln ( k max ) 0 0 2000 4000 6000 8000 10000 k max Jerry Gilfoyle The Configurations of CO 14 / 28

Legendre Polynomials ( m ℓ = 0) a k +2 = k ( k + 1) − A ( k + 2)( k + 1) a k m ℓ = 0 a 0 = a 1 = 1 ℓ � a k z k Θ = P ℓ ( z ) = z = cos θ even / odd First few polynomials. 5 cos 3 θ − 3 cos θ P 3 (cos θ ) = 1 � � P 0 (cos θ ) = 1 2 35 cos 4 θ − 30 cos 2 θ + 3 P 4 (cos θ ) = 1 � � P 1 (cos θ ) = cos θ 8 3 cos 2 θ − 1 63 cos 5 θ − 70 cos 3 θ + 15 cos θ P 2 (cos θ ) = 1 P 5 (cos θ ) = 1 � � � � 2 8 Jerry Gilfoyle The Configurations of CO 15 / 28

Spherical Harmonics ( m ℓ = m ) � 2 ℓ + 1 ( ℓ − m )! Θ( θ )Φ( φ ) = Y m ( ℓ + m )! P m ℓ (cos θ ) e im φ ℓ ( θ, φ ) = 4 π 1 Y 0 0 ( θ, φ ) = √ 4 π � � 3 3 Y 1 8 π sin θ e i φ Y − 1 8 π sin θ e − i φ 1 ( θ, φ ) = − ( θ, φ ) = 1 � 3 Y 0 1 ( θ, φ ) = 4 π cos θ Jerry Gilfoyle The Configurations of CO 16 / 28

Is Carbon Monoxide A Rigid Rotator? Excited states of carbon monoxide (CO) can be observed by measuring the absorption spectrum shown below. The molecule can both vibrate and rotate at the same time. The rotational energy states of a rigid rotator are E ℓ = � 2 2 I ℓ ( ℓ + 1) where I is the moment of inertia. The vibrational part of the energy is described by the harmonic oscillator so E n = ( n + 1 2 ) � ω 0 with ∆ E = � ω 0 = 0 . 25 ± 0 . 05 eV from our previous results. How do you get the expression above for the rotational energy? Is CO a rigid rotator? Carbon−Monoxide Spectrum Absorption 0.2550 0.2600 0.2650 0.2700 0.2750 Energy (eV) Jerry Gilfoyle The Configurations of CO 17 / 28

Is Carbon Monoxide A Rigid Rotator? Excited states of carbon monoxide (CO) can be observed by measuring the absorption spectrum shown below. The molecule can both vibrate and rotate at the same time. The rotational energy states of a rigid rotator are E ℓ = � 2 2 I ℓ ( ℓ + 1) where I is the moment of inertia. The vibrational part of the energy is described by the harmonic oscillator so E n = ( n + 1 2 ) � ω 0 with ∆ E = � ω 0 = 0 . 25 ± 0 . 05 eV from our previous results. How do you get the expression above for the rotational energy? Is CO a rigid rotator? Carbon−Monoxide Spectrum Absorption 0.2550 0.2600 0.2650 0.2700 0.2750 Energy (eV) Jerry Gilfoyle The Configurations of CO 17 / 28

Summary So Far p 2 2 µ = − � 2 � � 1 ∂ r 2 ∂ r r 2 2 µ ∂ r ∂ r 2 µ r 2 = − � 2 L 2 ∂ 2 � 1 ∂ � sin θ ∂ � 1 � + r 2 sin θ r 2 sin 2 θ ∂φ 2 2 µ ∂θ ∂θ m ℓ = 0 , ± 1 2 , ± 2 2 , ± 3 2 , ± 4 2 , ± 5 2 , ... m 2 � � � � − 1 ∂ sin θ ∂ ℓ + Θ = A Θ A = ℓ ( ℓ + 1) sin 2 θ sin θ ∂θ ∂θ L 2 | φ s � = � 2 ℓ ( ℓ + 1) | φ s � Jerry Gilfoyle The Configurations of CO 18 / 28

L 2 and L z The Eigenvalues of ˆ Jerry Gilfoyle The Configurations of CO 19 / 28