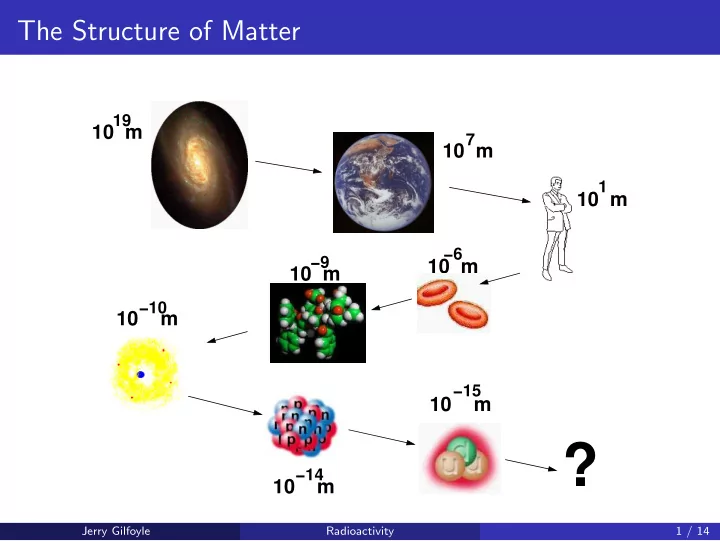

The Structure of Matter 19 10 m 7 10 m 1 10 m −6 −9 10 m 10 m −10 10 m −15 10 m ? −14 10 m Jerry Gilfoyle Radioactivity 1 / 14
Radioactivity and Nuclear Decay At the end of the nineteenth cen- tury Henri Becquerel discovers the spontaneous emission of ‘rays’. The surprise was that no energy in- put was required. These rays carry off huge amounts of energy. Some examples of ‘rays’. Original Photographic Plate Developed by Henri Becquerel. 212 208 4 Po Pb + He Pb + He (α) 84 82 2 212 212 Bi Po + e (β) + ν (undetected) e 83 84 137 137 ν e Cs Ba(0.662 keV) + e + (undetected) 55 56 137 Ba(0.0 keV) + γ 56 Jerry Gilfoyle Radioactivity 2 / 14
Why Should You Care? 1 Massive release of energy from a small amount of material. Weapons Energy source 2 How can we explain it? − → Why does the Sun shine? 3 Gobs of current uses. Food treatments. 1 Smoke detectors. 2 Medical applications (PET scans). 3 Environmental, medical, and biological monitoring. 4 Jerry Gilfoyle Radioactivity 3 / 14
The 4 He − 234 90 Th Potential 40 α - Th Potential Blue - known Red - a guess 20 V ( MeV ) 0 - 20 - 40 0 10 20 30 40 50 60 70 r ( fm ) Jerry Gilfoyle Radioactivity 4 / 14
Rutherford Scattering ZnS Microscope Collimator Alpha source Scattered helium Alpha beam Thorium target 210 4 206 Po He + Pb 84 2 82 Jerry Gilfoyle Radioactivity 5 / 14
The 4 He − 234 90 Th Potential 40 α - Th Potential Blue - known Red - a guess 20 V ( MeV ) 0 - 20 - 40 0 10 20 30 40 50 60 70 r ( fm ) Jerry Gilfoyle Radioactivity 6 / 14
Milking the Cow This ‘clock’ ticks by producing a short-lived, radioactive material. 137 Start with a liquid containing the ra- Cs − e 55 dioactive isotope 137 Cs that decays very slowly. excited state (0.662 MeV) 137 Cs → e − + 137 Ba ( 0 . 662 MeV ) γ ground state The number “0.662 MeV” means 137 56 Ba there is still energy (0.662 MeV) stored in the Ba-137 nucleus. Decay scheme of cesium-137. The excited Ba-137 then emits a high-energy photon or gamma ray to reach the stable ground state of 137 Ba . 137 Ba ( 0 . 662 ) → 137 Ba ( 0 . 0 )+ γ Jerry Gilfoyle Radioactivity 7 / 14
Geiger-Muller Tube A Geiger-Muller tube (or GM tube) is the sensing element of a Geiger counter instrument that can detect a single particle of ionizing radiation. It is a type of gaseous ionization detector with an operating voltage in the Geiger plateau. Jerry Gilfoyle Radioactivity 8 / 14
Using the Reduced χ 2 The χ 2 and reduced χ 2 are defined as N (( y i − f ( x i )) 2 χ 2 = � σ 2 i i =1 and χ 2 reduced χ 2 = N − d . o . f where N is the number of data points. In Mathematica the esti- mated variance is equal to the re- duced χ 2 if the proper weighting is used. R. Muto, et al. , Phys. Rev. Lett., 98 , 042501 (2007). Jerry Gilfoyle Radioactivity 9 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random 2 independent of each other Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random 2 independent of each other 3 continuous Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random 2 independent of each other 3 continuous 4 can be positive or negative Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random 2 independent of each other 3 continuous 4 can be positive or negative Do these conditions apply for radioactive decay? Jerry Gilfoyle Radioactivity 10 / 14
Probability Distribution Functions When Do You Use a Gaussian Probability Distribution Function? When variations in a measurement are 1 random 2 independent of each other 3 continuous 4 can be positive or negative Do these conditions apply for radioactive decay? NO! Jerry Gilfoyle Radioactivity 10 / 14
Poisson Statistics P ( m : n , p ) = 1 m ! µ m e − µ µ = np m - no. of events µ - average n - no. of trials p - probability of an event Probability of a discrete event occurring m times in a particular time period. Jerry Gilfoyle Radioactivity 11 / 14
Poisson Statistics P ( m : n , p ) = 1 m ! µ m e − µ µ = np m - no. of events µ - average n - no. of trials p - probability of an event Probability of a discrete event occurring m times in a particular time period. Number of soldiers killed by horse-kicks each year in Prussian cavalry corp (famous example in by a book of Ladislaus Josephovich Bortkiewicz (1868-1931)). Number of yeast cells for brewing Guinness (William Sealy Gosset (1876-1937)). The number of phone calls arriving at a call center per minute. The number of deaths per year in a given age group. The number of jumps in a stock price in a given time interval. The number of mutations in a given stretch of DNA after a certain amount of radiation. The proportion of cells infected at a given multiplicity of infection. Jerry Gilfoyle Radioactivity 11 / 14
Probability Distributions Binomial distribution: n ! m !( n − m )! p m q n − m P ( m ; n , p ) = q = 1 − p n - total number of events; m - number of events of probability p For p << 1 one obtains the Poisson distribution P ( m ; n , p ) = 1 m ! µ m e − µ µ = np What is the difference between a Gaussian distribution and a Poisson? Gaussian - random, independent, continuous variations. Poisson - discrete, random, positive variations. Jerry Gilfoyle Radioactivity 12 / 14
Semi-log Plots Time dependence of the Semi-log plot reveals the back- 137 Ba ( 0 . 662 ) decay on a lin- ground is significant. ear scale. Radioactive Decay Radioactive Decay 5000 137 Ba ( 0.662 ) decay 137 Ba ( 0.662 ) decay 4000 χ 2 / ν = 2.6 1000 χ 2 / ν = 2.6 t 1 / 2 = 2.65 ± 0.02 min 3000 t 1 / 2 = 2.65 ± 0.02 min 100 N N No background? 2000 10 1000 Background! 1 0 0 10 20 30 40 50 60 0 10 20 30 40 50 60 t ( min ) t ( min ) Jerry Gilfoyle Radioactivity 13 / 14
Semi-log Plots Time dependence of the Semi-log plot reveals the back- 137 Ba ( 0 . 662 ) decay on a lin- ground is significant. ear scale. Radioactive Decay Radioactive Decay 5000 137 Ba ( 0.662 ) decay 137 Ba ( 0.662 ) decay 4000 χ 2 / ν = 2.6, χ 2 / ν = 8.7 1000 χ 2 / ν = 2.6 t 1 / 2 = 2.65 ± 0.02 min ( red ) 3000 t 1 / 2 = 2.65 ± 0.02 min t 1 / 2 = 2.90 ± 0.03 min ( green ) 100 N N No background? 2000 10 1000 Background! 1 0 0 10 20 30 40 50 60 0 10 20 30 40 50 60 t ( min ) t ( min ) Jerry Gilfoyle Radioactivity 14 / 14
Recommend
More recommend