Eigenvalues of random normal matrices Random normal matrix model: - PowerPoint PPT Presentation
Eigenvalues of random normal matrices Random normal matrix model: Droplets Example: concentric ellipses Local droplets 1 0.5 -1.5 -1 -0.5 0.5 -0.5 -1 hypotrochoids deltoid Definition: K is a local droplet if Hele-Shaw flow 1 0.5
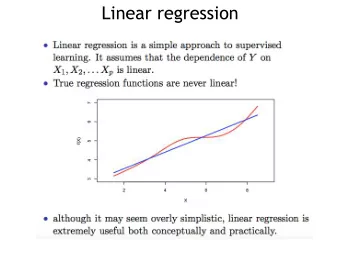
Eigenvalues of random normal matrices
Random normal matrix model:
Droplets Example:
concentric ellipses
Local droplets 1 0.5 -1.5 -1 -0.5 0.5 -0.5 -1 hypotrochoids deltoid Definition: K is a local droplet if
Hele-Shaw flow 1 0.5 -1.5 -1 -0.5 0.5 -0.5 -1
S-function and local droplets
Two pieces of the dynamics
?-function as conformal welding (mating)
centaurs
Examples of QDs bounded unbounded bounded . inversion d=0 d=1 . . . . d=2 d=1 limacons Neumann ovals wings
Example: 7 cardioids in ellipse
Connectivity bounds
Examples
Comments:
Bers slice for hexagonal torus
Inside the droplet • Convergence of fluctuations to a Gaussian field. Use of RNM model to approximate various objects related to GFF • Universality laws at regular points in the bulk and boundary, some types of singular points in the bulk
References • Based on joint work with Seung Yeop Lee. I thank Seung Yeop for pictures and crucial contributions • Use of conformal dynamics was inspired by a paper by Khavinson and Swiatek • Interesting analogy with some work in dimer model (Kenyon, Okounkov, Sheffield)
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.