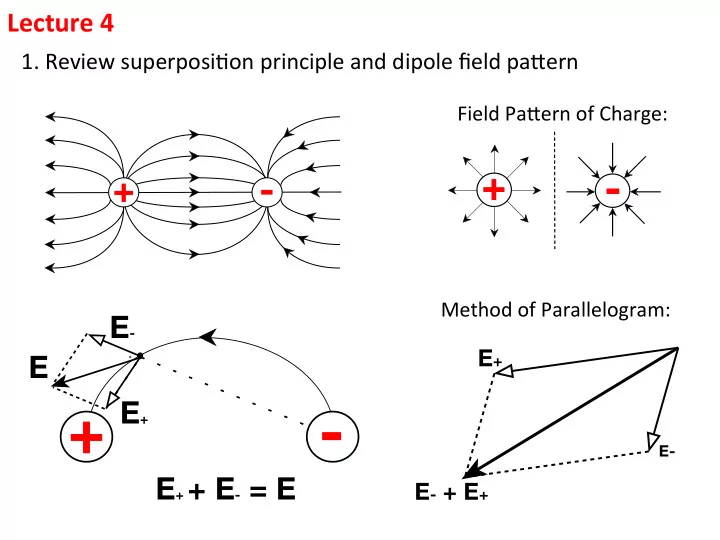
e e e e e e e b t z i 4 1il sa lia b7 dq p rnqrrluot leq
play

+ - E + E- E + + E - = E E - + E + 'b 't .Z .I 4"1il sA - PowerPoint PPT Presentation

Oct 22, 2022 •386 likes •479 views

Lecture 4 1. Review superposi.on principle and dipole field pa5ern Field Pa5ern of Charge: + - + - Method of Parallelogram: E - E + E + - E + E- E + + E - = E E - + E

  1. Lecture ¡4 ¡ 1. ¡Review ¡superposi.on ¡principle ¡and ¡dipole ¡field ¡pa5ern ¡ Field ¡Pa5ern ¡of ¡Charge: ¡ + - + - Method ¡of ¡Parallelogram: ¡ E - E + E + - E + E- E + + E - = E E - + E +

  2. 'b 't .Z .I 4"1il sA lia 'b7- dq p"rnqrrluot leq] pue b ,(q p"rnqrrtuot plerJ eql Jo epnlrutetu aql a;eduro3 'd lulod dtetlrqre uE tE III uor8at ul plalJ aql raprsuoJ {la-fi uor8a; aarqt olul srxe-x eql apnlp r{aqUa;n8g aq} uI ulrAorls sE b7- pue b satreql af,Jnos oIAl ualr3 -'l Clicker ¡4-­‑1 ¡ l*fr&YW

  3. Clicker ¡401: ¡Dipole ¡field ¡pa5ern ¡and ¡dipole ¡interac.on ¡ Lecture 5 Dipole field pattern and dipole interactions Lec5-1 Sketch a dipole field pattern Consider a dipole centered at the origin. A parallelogram of E field vectors due to the dipole charges has been constructed at point A . y B ~ E + A ~ ~ E net E − x Please sketch in your notebook the parallelogram formed by the field vectors at B. Wait. At the appropriate time discuss the parallelogram construction with your neighbour. Complete the parallelogram construction and label the three field vectors. Enter your clicker answer. Choice Have you completed your parallelogram construction at B? 1 Yes 2 No

  4. Field ¡at ¡a ¡point ¡P ¡ P + s − s 2 2 x s -q +q r where: ✏ = s E P = E + + E − 2 r kq kq = 2 ) 2 − ( r − s ( r + s 2 ) 2  � 1 1 = kq (1 − ✏ ) 2 − r 2 (1 + ✏ ) 2

  5. Digression ¡on ¡small ¡epsilon ¡expansion ¡ (1 − ✏ ) 2 = 1 − 2 ✏ + ✏ 2 = 1 − 2 ✏ + O ( ✏ 2 ) ≈ 1 − 2 ✏ (1 − ✏ ) 3 = 1 − 3 ✏ + 3 ✏ 3 + ✏ 3 = 1 − 3 ✏ + O ( ✏ 2 ) ≈ 1 − 3 ✏ General ¡Formula: ¡ ¡ (1 − ✏ ) a = 1 − a ✏ + O ( ✏ 2 ) ≈ 1 − a ✏ 1 Where ¡a ¡is ¡nega.ve: ¡ 1 − ✏ = 1 + ✏ (1 − ✏ )(1 + ✏ ) ≈ (1 − ✏ 2 ) ≈ 1 Product: ¡ So ¡the ¡general ¡formula ¡above ¡works ¡for ¡both ¡posi.ve ¡and ¡nega.ve! ¡ (1 − ✏ ) a ≈ 1 − a ✏

  6. Digression ¡on ¡small ¡epsilon ¡expansion ¡con4nued... ¡ Examples: ¡ 1 1 (1 − ✏ ) 2 = 1 − (2 ✏ ) ≈ 1 + 2 ✏ 1 1 (1 + ✏ ) 2 = 1 + 2 ✏ ≈ 1 − 2 ✏ − s + s P At ¡P ¡(from ¡slide ¡2): ¡ 2 2 x -q s +q r  1 1 � E P = kq ✏ = ( s/ 2) (1 − ✏ ) 2 − r 2 (1 + ✏ ) 2 x ⇣ s = 2 s ⌘ [ ] = (1 + 2 ✏ ) − (1 − 2 ✏ ) = 4 ✏ = f 2 x x E = kq x 2 · 2 s x = 2 kqs = 2 kp Dipole: ¡ p = qs x 3 x 3

  7. More ¡on ¡dipoles... ¡ E dipole ~ = ~ P 1 + ~ E + E − P 1 P 1 E + dir of E P 1 : ( − ˆ x ) P 1 E = 2 E + cos ↵ ~ E − = 2 × kq r 2 · s/ 2 = kqs r r 3 Dipole ¡in ¡Uniform ¡E: ¡ F dipole = ~ ~ F + q + ~ F − q = q ~ E − q ~ E = 0

  8. Uniform ¡dipole ¡in ¡uniform ¡E-­‑field ¡con.nued... ¡ F + F − α τ = Fd = Eqd = Eqs sin α ⌧ = ⌧ ˆ ~ n = ( Ep sin ↵ )ˆ n p × ~ = ~ E Direc.on: ¡CW ¡

  9. Is ¡electric ¡field ¡real? ¡ Source ¡creates ¡field: ¡field ¡spreads ¡out ¡with ¡the ¡speed ¡of ¡light. ¡ ¡Time ¡taken ¡to ¡spread ¡out ¡1 ¡foot: ¡ 0 . 3 3 × 10 8 = 10 − 9 sec = ns ∆ t ≈ e + e − system e + + e − → γγ 2 kp r Dipole ¡field ¡ r 3 At ¡t=0, ¡reac.on ¡occurs ¡ à ¡dipole ¡system ¡dissolves ¡ At ¡P: ¡Electric ¡field ¡due ¡to ¡the ¡dipole ¡con.nues ¡to ¡be ¡present ¡for ¡ t=0 ¡ à ¡t1 ¡= ¡r/c ¡

Recommend

More recommend