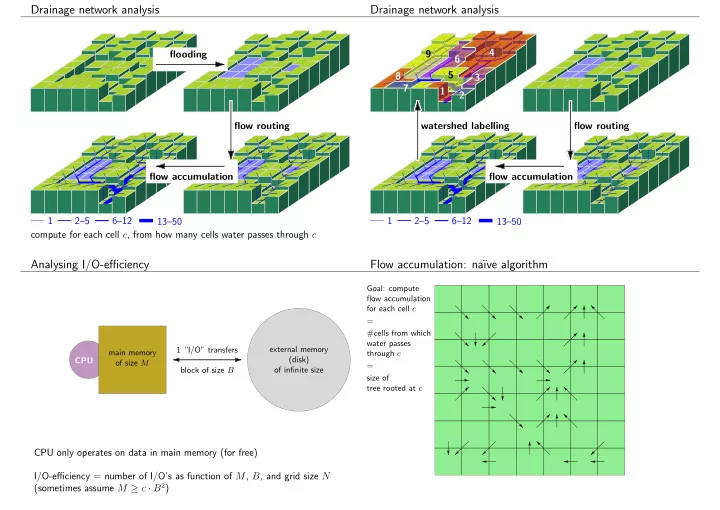

Drainage network analysis Drainage network analysis 4 flooding 9 6 5 8 3 7 1 2 flow routing watershed labelling flow routing flow accumulation flow accumulation 1 2–5 6–12 1 2–5 6–12 13–50 13–50 compute for each cell c , from how many cells water passes through c Analysing I/O-efficiency Flow accumulation: na¨ ıve algorithm Goal: compute flow accumulation for each cell c = #cells from which water passes 1 “I/O” transfers external memory main memory through c (disk) CPU of size M = block of size B of infinite size size of tree rooted at c CPU only operates on data in main memory (for free) I/O-efficiency = number of I/O’s as function of M , B , and grid size N (sometimes assume M ≥ c · B 2 )
Flow accumulation: na¨ ıve algorithm Flow accumulation: na¨ ıve algorithm Goal: compute Goal: compute 1 1 1 2 flow accumulation flow accumulation 1 for each cell c for each cell c = = 1 1 1 2 1 #cells from which #cells from which water passes water passes 1 1 2 2 through c through c = = size of size of 1 1 2 2 tree rooted at c tree rooted at c 1 1 2 2 1 2 Flow accumulation: na¨ ıve algorithm Row-by-row scan Goal: compute Goal: compute 6 flow accumulation 1 1 1 1 2 1 flow accumulation 1 1 1 1 1 1 1 for each cell c for each cell c = = 2 5 1 2 1 1 1 1 1 1 1 1 #cells from which #cells from which water passes water passes 5 5 1 1 1 1 1 1 1 through c through c = = size of size of 5 5 1 1 1 1 1 1 1 tree rooted at c tree rooted at c 5 5 1 1 1 1 1 1 1 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Row-by-row scan Row-by-row scan Goal: compute flow accumulation 1 1 1 1 3 35 1 for each cell c = 1 2 2 2 1 32 1 #cells from which water passes 1 6 1 1 1 30 1 through c = size of 1 4 7 2 28 1 1 tree rooted at c 1 1 13 1 22 1 1 1 1 1 19 1 1 1 Running time: Θ( N ) 3 3 1 1 4 3 1 N = #cells in grid Row-by-row scan Z-order scan Θ( N ) I/O’s in the worst case ≈ 1 year for 28 GB grid N = #cells in grid
Z-order scan Z-order scan Z-order scan Z-order scan on Z-order file √ B While working on a block, have its neighbours in memory too B = #bytes in one I/O
Z-order scan on Z-order file Z-order scan on Z-order file √ √ B B While working While working on a block, on a block, have its have its neighbours in neighbours in memory too memory too Only long paths require additional swapping B = #bytes in one I/O B = #bytes in one I/O Worst-case terrains vs. real terrains Worst-case terrains vs. real terrains Worst-case, size N Worst-case, size 4 N Worst-case, size N Worst-case, size 4 N √ Ω( N ) big bends Realistic, size N Realistic, size 4 N Q ′ = Q scaled by factor 3. Far cells of Q : cells on boundary of Q ′ where water from Q collects. Θ(1) big bends In the worst case, maximum number of far cells grows with resolution. N = #cells in grid N = #cells in grid
Worst-case terrains vs. real terrains Z-order scan on Z-order file Realistic, size N Realistic, size 4 N √ B While working on a block, have its neighbours in memory too Θ( N/B ) I/Os Only long paths require additional swapping N/B blocks × Q ′ = Q scaled by factor 3. γ swaps × Far cells of Q : cells on boundary of Q ′ where water from Q collects. 9-block window = Confluence assumption: number of far cells for any square Q ≤ constant γ Θ( N/B ) I/Os ≈ few hours N = #cells in grid N = #cells in grid B = #bytes in one I/O Flow accumulation by scanning in practice (row, column) ↔ Z-index theoretical analysis experiments 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 algorithm file order worst case ‘realistic’ bytes per cell time (mins) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 √ row-by-row scan row by row O ( N ) O ( N/ B ) tenthousands 111 (0) (1) (4) (5) (16) (17) (20) (21) Z-order scan row by row O ( N ) O ( N/B ) ∗ thousands 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 √ Z-order scan Z-order O ( N/ B ) O ( N/B ) hundreds 41 (2) (3) (6) (7) (18) (19) (22) (23) 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 bytes of disk I/O per cell calculated based on: N = 2 32 , M = 1 GB, B = 16 to 64KB time: 3 GHz Pentium, one disk for data + scratch, N = 3 . 5 · 10 9 (Neuse), M = 1 GB (8) (9) (12) (13) (24) (25) (28) (29) *) needs tall cache: M ≥ cB 2 0 1 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 1 (10) (11) (14) (15) (26) (27) (30) (31) Easy implementation: • needs efficient conversion ( row nr. , column nr. ) ↔ index in Z-order 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 • Z-order scan → good caching by OS, no need to tune to hardware / implement I/O-control (32) (33) (36) (37) (48) (49) (52) (53) 1 0 1 1 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 Z-order-traversal has many other applications, e.g.: (34) (35) (38) (39) (50) (51) (54) (55) • I/O-efficient matrix operations 1 1 0 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 • I/O-efficient algorithms and data structures for geographic maps (40) (41) (44) (45) (56) (57) (60) (61) 1 1 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 (42) (43) (46) (47) (58) (59) (62) (63) N = #cells in grid B = #bytes in one I/O
(row, column) ↔ Z-index Flow accumulation: separator-based algorithm √ √ Quick conversion through look-ups in tables of size N (example: N = 16 ) Separator cells: each √ row number column number spread rowdigits coldigits Θ( M ) -th row/column 0110 0011 0000 0 0 0 0 0 0 0 00 00 → look up in look up in 0001 0 0 0 0 0 0 1 00 01 divide grid into Θ( N/M ) spread spread 0010 0 0 0 0 1 0 0 01 00 subgrids of size Θ( M ) 0010100 0000101 0011 0 0 0 0 1 0 1 01 01 append 0 0100 0 0 1 0 0 0 0 00 10 00101000 0 0 1 0 0 0 1 0101 00 11 0 0 1 0 1 0 0 0110 01 10 add 0 0 1 0 1 0 1 00101101 0111 01 11 1000 1 0 0 0 0 0 0 10 00 Z-index 1001 1 0 0 0 0 0 1 10 01 1010 1 0 0 0 1 0 0 11 00 first half second half 1011 1 0 0 0 1 0 1 11 01 0010 1101 1100 1 0 1 0 0 0 0 10 10 look up in look up in look up in look up in 1 0 1 0 0 0 1 1101 10 11 √ rowdigits coldigits rowdigits coldigits 1 0 1 0 1 0 0 1110 11 10 Θ( M ) 01 00 10 11 1111 1 0 1 0 1 0 1 11 11 concatenate concatenate 0110 0011 can be adapted to non-square grids row number column number N = #cells in grid M = main memory size Flow accumulation: separator-based algorithm Flow accumulation: separator-based algorithm input input 1. move flow from interior 1. move flow from interior of subgrids to separators of subgrids to separators 1 1 and compute flow connec- and compute flow connec- tions between separators tions between separators 3 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 √ √ 1 1 1 1 1 1 Θ( M ) Θ( M ) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 separator separator separator separator 1 1 1 1 1 1 1 1 1 1 1 1 1 1 flow accumul. flow directions flow accumul. flow directions N = #cells in grid M = main memory size N = #cells in grid M = main memory size
Flow accumulation: separator-based algorithm Flow accumulation: separator-based algorithm input input 1. move flow from interior 1. move flow from interior of subgrids to separators of subgrids to separators 1 1 and compute flow connec- and compute flow connec- tions between separators tions between separators 3 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 √ √ 1 1 1 1 1 1 Θ( M ) Θ( M ) 1 1 1 1 1 1 4 2 4 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 separator separator separator separator 1 1 1 1 1 1 1 1 1 1 1 1 1 1 flow accumul. flow directions flow accumul. flow directions N = #cells in grid M = main memory size N = #cells in grid M = main memory size Flow accumulation: separator-based algorithm Flow accumulation: separator-based algorithm input 1. move flow from interior 1. move flow from interior of subgrids to separators of subgrids to separators and compute flow connec- and compute flow connec- tions between separators tions between separators 1 1 1 1 1 1 1 1 1 1 1 1 5 1 √ √ 1 1 1 1 1 1 Θ( M ) Θ( M ) 1 1 1 1 1 1 4 2 1 1 1 1 1 1 1 4 2 5 1 1 1 1 1 1 1 1 1 1 1 1 3 1 separator separator separator separator 1 1 1 1 1 1 1 2 2 1 1 1 1 1 flow accumul. flow directions flow accumul. flow directions N = #cells in grid M = main memory size N = #cells in grid M = main memory size
Recommend
More recommend