dimension d v ( H ) most p oints H an shatter 10 10 5 - PowerPoint PPT Presentation

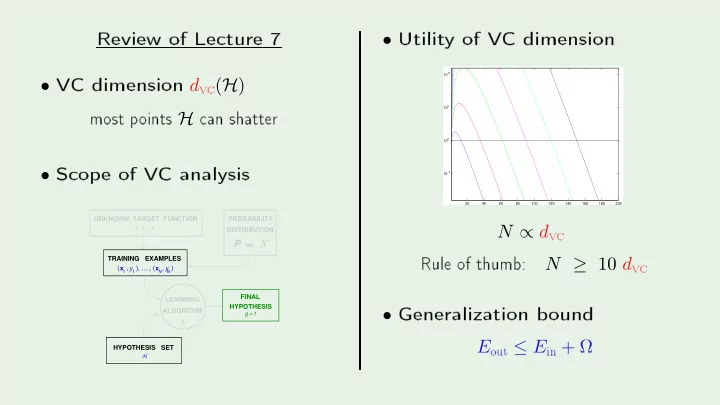
Review of Le ture 7 Utilit y of V C dimension V C dimension d v ( H ) • most p oints H an shatter 10 10 • 5 S op e of V C analysis 10 0 10 v • −5 10 Rule of thumb: v up 20 40 60 80 100 120 140 160 180 200 UNKNOWN TARGET FUNCTION PROBABILITY f: X Y DISTRIBUTION N ∝ d P X on Generalization b ound TRAINING EXAMPLES N ≥ 10 d x y x y ( , ), ... , ( , ) N N 1 1 out ≤ E in + Ω FINAL LEARNING HYPOTHESIS ALGORITHM • g ~ f ~ A E HYPOTHESIS SET H down

Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 8 : Bias-V a rian e T radeo� Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST Thursda y , Ap ril 26, 2012 •

Outline Bias and V a rian e • Lea rning Curves • Creato r: Y aser Abu-Mostafa - LFD Le ture 8 2/22 M � A L

App ro ximation-generalization tradeo� Small E : go o d app ro ximation of f out of sample. out Mo re omplex H = b etter han e of app ro ximating f Less omplex H = b etter han e of generalizing out of sample ⇒ Ideal H = { f } winning lottery ti k et ⇒ Creato r: Y aser Abu-Mostafa - LFD Le ture 8 3/22 M � A L

Quantifying the tradeo� V C analysis w as one app roa h: E out ≤ E in + Ω Bias-va rian e analysis is another: de omp osing E into out 1. Ho w w ell H an app ro ximate f 2. Ho w w ell w e an zo om in on a go o d h ∈ H Applies to real-valued ta rgets and uses squa red erro r Creato r: Y aser Abu-Mostafa - LFD Le ture 8 4/22 M � A L

Sta rt with E out out ( g ( D ) )= E x �� � 2 � g ( D ) ( x ) − f ( x ) E out ( g ( D ) ) � �� � 2 �� � � g ( D ) ( x ) − f ( x ) = E E D E D E x � �� � 2 �� g ( D ) ( x ) − f ( x ) = E x E D No w, let us fo us on: Creato r: Y aser Abu-Mostafa - LFD Le ture 8 5/22 �� � 2 � g ( D ) ( x ) − f ( x ) E D M � A L

The average hyp othesis T o evaluate E D �� � 2 � g ( D ) ( x ) − f ( x ) w e de�ne the `average' hyp othesis ¯ : g ( x ) � � g ( D ) ( x ) Imagine many data sets D 1 , D 2 , · · · , D K g ( x ) = E D ¯ K 1 � Creato r: Y aser Abu-Mostafa - LFD Le ture 8 6/22 g ( D k ) ( x ) g ( x ) ≈ ¯ K k =1 M � A L

Using ¯ g ( x ) �� � 2 � �� � 2 � g ( D ) ( x ) − f ( x ) g ( D ) ( x ) − ¯ = E D g ( x ) + ¯ g ( x ) − f ( x ) E D �� � 2 + � � 2 g ( D ) ( x ) − ¯ = E D g ( x ) g ( x ) − f ( x ) ¯ �� � � � g ( D ) ( x ) − ¯ + 2 g ( x ) g ( x ) − f ( x ) ¯ �� � 2 � Creato r: Y aser Abu-Mostafa - LFD Le ture 8 7/22 � � 2 g ( D ) ( x ) − ¯ = E D g ( x ) + g ( x ) − f ( x ) ¯ M � A L

Bias and va rian e va r ( x ) bias ( x ) �� � 2 � �� � 2 � �� � 2 � g ( D ) ( x ) − f ( x ) g ( D ) ( x ) − ¯ = E D g ( x ) + g ( x ) − f ( x ) ¯ E D Therefo re, � �� � � �� � out ( g ( D ) ) � �� � 2 �� � � g ( D ) ( x ) − f ( x ) = E x E E D E D = E x [ bias ( x ) + va r ( x )] bias va r Creato r: Y aser Abu-Mostafa - LFD Le ture 8 8/22 = + M � A L

The tradeo� bias = E x va r = E x �� � 2 � � �� � 2 �� g ( D ) ( x ) − ¯ g ( x ) − f ( x ) ¯ g ( x ) E D bias va r H f H f Creato r: Y aser Abu-Mostafa - LFD Le ture 8 9/22 ↓ H ↑ ↑ M � A L

Example: sine ta rget H 0 f Only t w o training examples! f :[ − 1 , 1] → R f ( x ) = sin( πx ) 2 T w o mo dels used fo r lea rning: 1.5 N = 2 1 0.5 0 H 0 : h ( x ) = b −0.5 Whi h is b etter, H 0 o r H 1 ? H 1 : h ( x ) = ax + b −1 Creato r: Y aser Abu-Mostafa - LFD Le ture 8 10/22 −1.5 −2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 M � A L

App ro ximation - H 0 versus H 1 H 0 H 1 2 2 1.5 1.5 1 1 0.5 0.5 0 0 out = 0 . 50 out = 0 . 20 −0.5 −0.5 −1 −1 E E Creato r: Y aser Abu-Mostafa - LFD Le ture 8 11/22 −1.5 −1.5 −2 −2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 M � A L

Lea rning - H 0 versus H 1 H 0 H 1 2 2 1.5 1.5 1 1 0.5 0.5 0 0 −0.5 −0.5 −1 −1 Creato r: Y aser Abu-Mostafa - LFD Le ture 8 12/22 −1.5 −1.5 −2 −2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 M � A L

PSfrag repla ements PSfrag repla ements -1 -1 -0.8 -0.8 -0.6 -0.6 -0.4 -0.4 -0.2 -0.2 0 0 0.2 0.2 0.4 0.4 0.6 0.6 0.8 0.8 1 1 -1 -1 Bias and va rian e - H 0 -0.8 -0.8 -0.6 -0.6 -0.4 -0.4 -0.2 -0.2 0 0 0.2 0.2 0.4 0.4 0.6 0.6 y y 0.8 0.8 g ( x ) ¯ 1 1 sin( πx ) Creato r: Y aser Abu-Mostafa - LFD Le ture 8 13/22 x x M � A L

PSfrag repla ements PSfrag repla ements -1 -1 -0.8 -0.8 -0.6 -0.4 -0.6 -0.4 -0.2 0 -0.2 0 0.2 0.2 0.4 0.4 0.6 Bias and va rian e - H 1 0.6 0.8 1 0.8 1 -8 -6 -3 -2 -4 -1 -2 0 0 1 2 g ( x ) ¯ y y 4 2 3 6 sin( πx ) Creato r: Y aser Abu-Mostafa - LFD Le ture 8 14/22 x x M � A L

PSfrag repla ements PSfrag repla ements -1 -0.8 -0.6 -0.4 -1 -0.2 0 -0.8 -0.6 0.2 0.4 -0.4 -0.2 0.6 0 0.8 1 0.2 0.4 -1 -0.8 0.6 and the winner is . . . 0.8 -0.6 -0.4 1 -3 -0.2 H 0 H 1 -2 0 -1 0.2 0 0.4 0.6 1 g ( x ) ¯ y y 2 0.8 g ( x ) ¯ 1 3 sin( πx ) sin( πx ) bias = 0 . 50 va r = 0 . 25 bias = 0 . 21 va r = 1 . 69 x x Creato r: Y aser Abu-Mostafa - LFD Le ture 8 15/22 M � A L

Lesson lea rned Mat h the `mo del omplexit y' to the data resour es , not to the ta rget omplexit y Creato r: Y aser Abu-Mostafa - LFD Le ture 8 16/22 M � A L

Outline Bias and V a rian e • Lea rning Curves • Creato r: Y aser Abu-Mostafa - LFD Le ture 8 17/22 M � A L

Exp e ted E and E out in Data set D of size N Exp e ted out-of-sample erro r out ( g ( D ) )] Exp e ted in-sample erro r in ( g ( D ) )] E D [ E Ho w do they va ry with N ? E D [ E Creato r: Y aser Abu-Mostafa - LFD Le ture 8 18/22 M � A L

PSfrag repla ements PSfrag repla ements 20 20 40 The urves 40 60 60 80 80 100 100 120 out 120 0.05 in 0.16 0.1 r r out Erro Erro E 0.18 0.15 e ted e ted E 0.2 0.2 E Exp in Exp 0.22 0.25 Numb er of Data P oints, N Numb er of Data P oints, N E Simple Mo del Complex Mo del Creato r: Y aser Abu-Mostafa - LFD Le ture 8 19/22 M � A L

PSfrag repla ements PSfrag repla ements 20 20 40 40 V C versus bias-va rian e 60 60 80 80 0.16 0.16 0.17 0.17 out out 0.18 0.18 va rian e generalization erro r 0.19 0.19 r r Erro Erro E E 0.2 0.2 in in e ted e ted 0.21 0.21 bias in-sample erro r Exp Exp 0.22 0.22 E E Numb er of Data P oints, N Numb er of Data P oints, N V C analysis bias-va rian e Creato r: Y aser Abu-Mostafa - LFD Le ture 8 20/22 M � A L

Linea r regression ase T x + Noisy ta rget y = w ∗ noise Data set D = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T X) − 1 X T y Linea r regression solution: w = (X In-sample erro r ve to r = X w − y `Out-of-sample' erro r ve to r = X w − y ′ Creato r: Y aser Abu-Mostafa - LFD Le ture 8 21/22 M � A L

PSfrag repla ements 0 20 40 60 80 100 0 Lea rning urves fo r linea 0.2 r regression 0.4 0.6 Best app ro ximation erro r = σ 2 0.8 1 out Exp e ted in-sample erro r = σ 2 � 1.2 1.4 r Erro E � Exp e ted out-of-sample erro r = σ 2 � 1 − d +1 1.6 in N σ 2 e ted 1.8 � Exp e ted generalization erro r = 2 σ 2 � d +1 1 + d +1 Exp 2 E N Numb er of Data P oints, N � N d + 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 8 22/22 M � A L