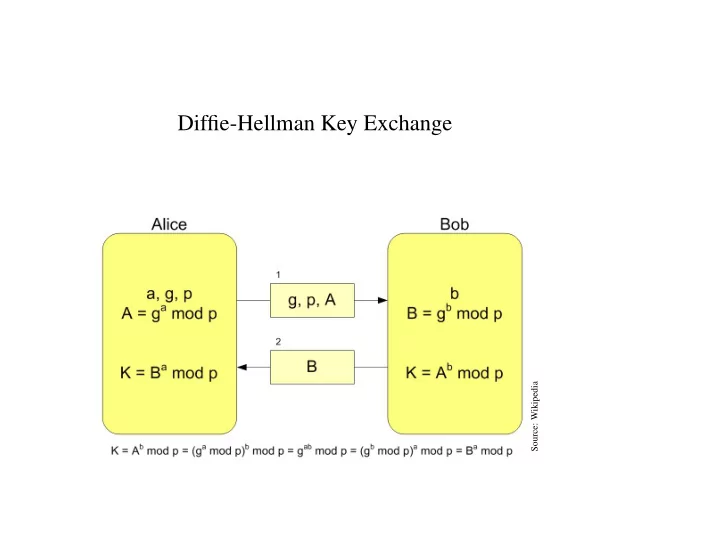
Diffie-Hellman Key Exchange Source: Wikipedia ElGamal Key - PowerPoint PPT Presentation

Diffie-Hellman Key Exchange Source: Wikipedia

ElGamal — Key Generator • Generate primes p and q as well as an element g ∈ Z ∗ p that generates the subgroup G q . • Choose a random x from { 0 , . . . , q − 1 } . • Compute h = g x . • Publish the public key � K = ( G q , q, g, h ) . • Retain the private key K = x .

ElGamal — Encryption Plaintext M , Public key � K = ( G q , q, g, h ) • M is considered to be an element of G • Choose a random y from { 0 , . . . , q − 1 } , then calculate c 1 = g y and c 2 = M · h y . • The ciphertext is then C = ( c 1 , c 2 ) .

ElGamal — Decryption Ciphertext C = ( c 1 , c 2 ) , Secret key K = x • Compute M = c 2 · c − x 1 x is the x th exponent of the inverse of c 1 in G q . where c − x = ( c 1 − 1 ) 1

Cramer-Shoup — Key Generator • Generate primes p and q , and the subgroup G q of Z ∗ p . Choose randomly two generators g 1 and g 2 of G q . • Choose six random values ( x 1 , x 2 , y 1 , y 2 , z 1 , z 2 ) from { 0 , . . . , q − 1 } . 2 , d = g y 1 1 g y 2 • Compute c = g x 1 1 g x 2 2 , and h = g z 1 1 g z 2 2 . • Publish the public key � K = ( G q , q, g 1 , g 2 , c, d, h ) . • Retain the private key K = ( x 1 , x 2 , y 1 , y 2 , z 1 , z 2 ) .

Cramer-Shoup — Encryption Plaintext M , Public key � K = ( G, q, g 1 , g 2 , c, d, h ) • M is considered to be an element of G • Choose a random k from { 0 , . . . , q − 1 } then calculate: – u 1 = g k 1 , u 2 = g k 2 – e = h k · M – α = H ( u 1 , u 2 , e ) , where H is the hash function – v = c k · d kα • Ciphertext is C = ( u 1 , u 2 , e, v ) .

Cramer-Shoup — Decryption Ciphertext C = ( u 1 , u 2 , e, v ) , Secret key K = ( x 1 , x 2 , y 1 , y 2 , z 1 , z 2 ) • Compute α = H ( u 1 , u 2 , e ) and verify that 2 ) α = v . 2 · ( u y 1 1 · u y 2 u x 1 1 · u x 2 If this test fails, further decryption is aborted and the output is rejected. • Otherwise, compute the plaintext as M = e · ( u z 1 1 u z 2 2 ) − 1 .