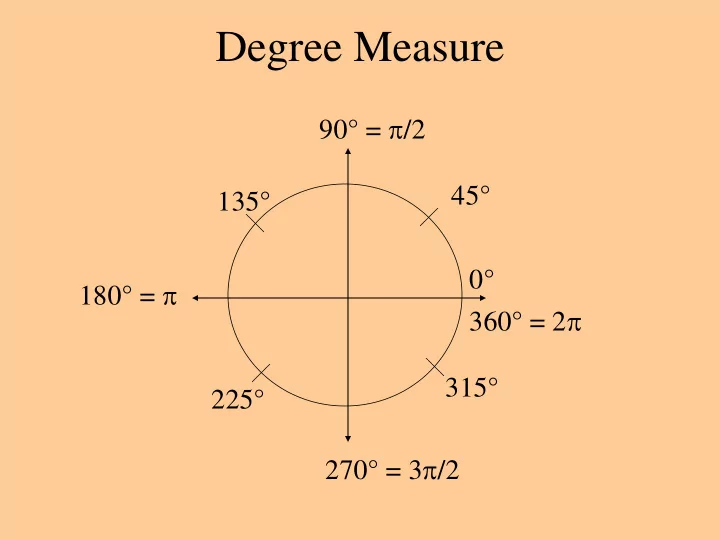
Degree Measure 90 = /2 45 135 0 180 = 360 = 2 315 225 270 = 3 - PowerPoint PPT Presentation

Degree Measure 90° =  /2 45° 135° 0° 180° =  360° = 2  315° 225° 270° = 3  /2

 radians = 180 degrees So,   180 180  Degrees = Radians 180 “If given degrees, multiply by  /180 to get radians.” 180 Radians = Degrees  “If given radians, multiply by 180/  to get degrees.”

Ex 6: Write each in radian measure as a multiple of  .  Degrees = Radians 180 A. 30° B. 150°        rad  5 5 30 180 6 rad 150 180 6 6 6 -1       20 180 9 rad C. - 20° 9

Ex 7: Convert each measure from degrees to radians. Round to three decimal places. A. 115 ° B. -216.35° 2.007 rad -3.776 rad C. 532° 9.285 rad

Ex 8: Write each in degree measure. 180 Radians = Degrees  A. 3  /2 B. 7  /6  30 7 180  90 3 180  = 210 °  = 270 °  6  2  15 7 180   = -105 ° C. -7  /12  12

Ex 9: Convert each measure from radians to degrees. Round to three decimal places. A.  /7 B. 15  /8  180  180   15 180 15 180     7 7  8 8  25 714  .  337 5 .  C. - 4.2    756  Homework: p.139 #26-48 even