
CSE 373: Disjoint sets h 10 14 9 2 4 7 11 8 8 4 i g 1 f e d c b a Example of the algorithm: Kruskal’s algorithm: example with a weighted graph 3 7 6 1 2 6 10 8 7 6 1 2 10 14 9 2 4 7 11 8 4 7 i h g f e d c b a Example of the algorithm: Kruskal’s algorithm: example with a weighted graph 3 2 14 Michael Lee b 11 8 8 4 i h g f e d c a 9 Example of the algorithm: Kruskal’s algorithm: example with a weighted graph 2 if it doesn’t introduce a cycle. Loop over edges, from smallest to largest. Use the edge only any already-visited node as the cost. Nearly identical to Dijkstra’s, except we use the distance to Last time... Review 1 Wednesday, Feb 28, 2018 7 4 2 9 2 4 7 11 8 8 4 i h g f e d c b a Example of the algorithm: Kruskal’s algorithm: example with a weighted graph 3 7 6 1 2 10 14 3 ◮ Prim’s algorithm: ◮ Kruskal’s algorithm:
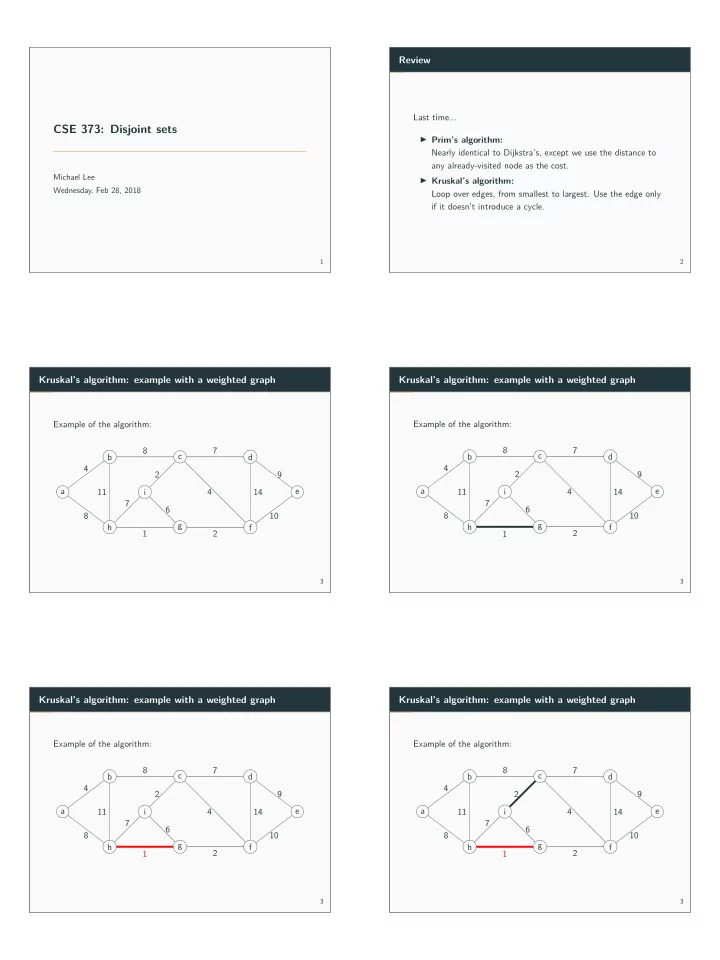
Kruskal’s algorithm: example with a weighted graph b 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a c 2 d e f g h i 4 1 10 8 i b c d e f g h 4 14 8 8 11 7 4 2 9 8 11 Example of the algorithm: 4 i 4 8 8 11 7 2 g 9 14 10 2 1 6 7 h f 7 6 4 2 9 14 10 2 1 7 e 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c d a Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a 1 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: b 10 c d e f g h i 2 14 8 h a b c d e f g i 9 4 8 8 11 7 4 2 4 8 3 4 h i 4 8 8 11 7 2 f 9 14 10 2 1 6 7 g e 11 1 7 4 2 9 14 10 2 6 d 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c 3
Kruskal’s algorithm: example with a weighted graph b 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a c 2 d e f g h i 4 1 10 8 i b c d e f g h 4 14 8 8 11 7 4 2 9 8 11 Example of the algorithm: 4 i 4 8 8 11 7 2 g 9 14 10 2 1 6 7 h f 7 6 4 2 9 14 10 2 1 7 e 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c d a Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a 1 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: b 10 c d e f g h i 2 14 8 h a b c d e f g i 9 4 8 8 11 7 4 2 4 8 3 4 h i 4 8 8 11 7 2 f 9 14 10 2 1 6 7 g e 11 1 7 4 2 9 14 10 2 6 d 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c 3
Kruskal’s algorithm: example with a weighted graph b 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a c 2 d e f g h i 4 1 10 8 i b c d e f g h 4 14 8 8 11 7 4 2 9 8 11 Example of the algorithm: 4 i 4 8 8 11 7 2 g 9 14 10 2 1 6 7 h f 7 6 4 2 9 14 10 2 1 7 e 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c d a Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a 1 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: b 10 c d e f g h i 2 14 8 h a b c d e f g i 9 4 8 8 11 7 4 2 4 8 3 4 h i 4 8 8 11 7 2 f 9 14 10 2 1 6 7 g e 11 1 7 4 2 9 14 10 2 6 d 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c 3
Kruskal’s algorithm: example with a weighted graph b 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a c 2 d e f g h i 4 1 10 8 i b c d e f g h 4 14 8 8 11 7 4 2 9 8 11 Example of the algorithm: 4 i 4 8 8 11 7 2 g 9 14 10 2 1 6 7 h f 7 6 4 2 9 14 10 2 1 7 e 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c d a Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a 1 6 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: b 10 c d e f g h i 2 14 8 h a b c d e f g i 9 4 8 8 11 7 4 2 4 8 3 4 h i 4 8 8 11 7 2 f 9 14 10 2 1 6 7 g e 11 1 7 4 2 9 14 10 2 6 d 7 3 Kruskal’s algorithm: example with a weighted graph Example of the algorithm: a b c 3
Kruskal’s algorithm: example with a weighted graph Interlude: What is a set? Runtime analysis: Example of the algorithm: 4 Kruskal’s algorithm: analysis use a general-purpose comparison sort Putting it all together: 5 The DisjointSet ADT 6 Review: what is a set? 3 Interesting note: sets come up all the time in math. 7 The DisjointSet ADT Properties of a disjoint-set data structure: difgerent sets. Each set must be disjoint . What is a representative? Any sort of unique “identifjer”. Examples: “representative” Kruskal’s algorithm: analysis Note: assume that... 7 i 4 6 11 8 8 4 h 9 g f e d c b a 2 7 14 10 1 2 8 def kruskal(): for (v : vertices): makeMST(v) sort edges in ascending order by their weight mst = new SomeSet<Edge>() for (edge : edges): if findMST(edge.src) != findMST(edge.dst): union(edge.src, edge.dst) mst.add(edge) return mst ◮ makeMST(v) takes O ( t m ) time ◮ findMST(v) : takes O ( t f ) time ◮ union(u, v) : takes O ( t u ) time ◮ Making the | V | MSTs takes O ( | V |· t m ) time ◮ Sorting the edges takes O ( | E |· log ( | E | )) time, assuming we But wait, what exactly is t m , t f , and t u ? How exactly do we ◮ The fjnal loop takes O ( | E |· t f + | V |· t u ) time implement makeMST(v) , findMST(v) , and union(u, v) ? We can do so using a new ADT called the DisjointSet ADT! O ( | V | · t m + | E |· log ( | E | ) + | E |· t f + | V |· t u ) ◮ A disjoint-set data structure maintains a collection of many ◮ An item may not be contained within multiple sets. ◮ A set is a “bag” of elements arranged in no particular order. ◮ A set may not contain duplicates. ◮ Each set is associated with some representative . We implemented a set in project 2: ChainedHashSet ◮ We could pick some arbitrary element in the set to be the ◮ We could assign each set some unique integer id.
print(findSet(a)) print(findSet(d)) union(a, c) union(b, d) print(findSet(a) == findSet(c)) print(findSet(a) == findSet(d)) union(c, b) print(findSet(a) == findSet(d)) print(findSet(a)) print(findSet(d)) union(a, c) union(a, c) union(b, d) union(b, d) print(findSet(a) == findSet(c)) print(findSet(a) == findSet(c)) print(findSet(a) == findSet(d)) print(findSet(a) == findSet(d)) union(c, b) union(c, b) print(findSet(a) == findSet(d)) print(findSet(a) == findSet(d)) union(c, b) union(c, b) print(findSet(a) == findSet(d)) print(findSet(a) == findSet(d)) 10 d e Rep: 4 c b a c Rep: 3 Rep: 2 Rep: 1 Rep: 0 d 10 b b d c The DisjointSet ADT Example: Rep: 0 Rep: 1 Rep: 4 a a e Rep: 4 Rep: 3 A disjoint-set has the following core operations: Rep: 1 Rep: 0 Example: The DisjointSet ADT e Rep: 2 The DisjointSet ADT 10 Example: 10 e d c b a The DisjointSet ADT Rep: 0 9 representative of this new set. We (arbitrarily) pick one of the two representatives to be the containing y . We combine these two sets together into one. the representative of that set. We assign that set a representative. The DisjointSet ADT Example: Rep: 1 Rep: 3 Example: The DisjointSet ADT 10 Rep: 2 e d c b a Rep: 4 makeSet(a) makeSet(b) makeSet(c) ◮ makeSet(x) – Creates a new set where the only member is x . makeSet(d) makeSet(e) ◮ findSet(x) – Looks up the set containing x . Then, returns ◮ union(x, y) – Looks up the set containing x and the set makeSet(a) makeSet(a) makeSet(b) makeSet(b) makeSet(c) makeSet(c) makeSet(d) makeSet(d) makeSet(e) makeSet(e) print(findSet(a)) print(findSet(d)) makeSet(a) makeSet(a) makeSet(b) makeSet(b) makeSet(c) makeSet(c) makeSet(d) makeSet(d) makeSet(e) makeSet(e) print(findSet(a)) print(findSet(a)) print(findSet(d)) print(findSet(d)) union(a, c) union(a, c) union(b, d) union(b, d) print(findSet(a) == findSet(c)) print(findSet(a) == findSet(c)) print(findSet(a) == findSet(d)) print(findSet(a) == findSet(d))
Recommend
More recommend