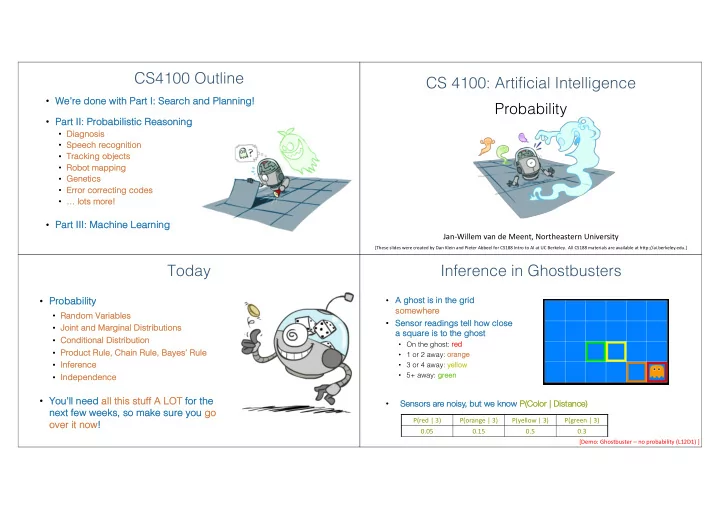

CS4100 Outline CS 4100: Artificial Intelligence • We We’re re done one with h Part art I: Search earch and and Planni anning ng! Probability • Part II: Probabilist stic Reaso soning • Diagnosi sis • Spe Speech r recogn gniti tion • Tracki king objects • Ro Robot mapping • Ge Geneti tics • Er Error c correcti ting c g code des • … … lots s more! • Pa Part III: Machine Learning Jan-Willem van de Meent, Northeastern University [These slides were created by Dan Klein and Pieter Abbeel for CS188 Intro to AI at UC Berkeley. All CS188 materials are available at http://ai.berkeley.edu.] Today Inference in Ghostbusters • Pr • A ghost st is s in the grid Proba babi bility somewhere so • Ra Random Variables • Senso sor readings s tell how close se • Jo Joint and Marginal Dist stributions a sq square is s to the ghost st • Conditional Dist stribution • On the ghost: re red • Product Rule, Chain Rule, Baye yes’ s’ Rule • 1 or 2 away: or orang ange • In • 3 or 4 away: ye Infe ference yellow • 5+ away: gr • In green Inde depe pende dence • Yo You’ll need d all this s st stuff A LOT fo for th the Sensors are noisy, but we kn know P( P(Color | Distance) • next xt few weeks, ks, so so make ke su sure yo you go go P(red | 3) P(orange | 3) P(yellow | 3) P(green | 3) ove ver it now! 0.05 0.15 0.5 0.3 [Demo: Ghostbuster – no probability (L12D1) ]
Ghostbusters Uncertainty • General si situation: • Obse serve ved va variables s (evi vidence): Agent knows certain things about the state of the world (e.g., sensor readings or symptoms) • Unobse serve ved va variables: s: Agent needs to reason about other aspects (e.g. where an object is or what disease is present) • Mo Model: Agent knows something about how the known variables relate to the unknown variables • Probabilist stic reaso soning give ves s us s a framework k for managing our beliefs s and kn knowledge Random Variables Probability Distributions • A A random va variable is s so some asp spect of the world about • Asso ssociate a probability y with each va value which we (may) y) have ve uncertainty • R = Is s it raining ? • T = Is s it hot or cold ? Temperature Te We Weather • D = How long will it take ke to drive ve to work ? • L = Where is s the ghost st ? W P • We We denot enote e random va variables s wit with cap capital al let etter ers T P sun 0.6 hot 0.5 • Like ke va variables s in a CSP, random va variables s have ve domains rain 0.1 cold 0.5 fog 0.3 • R in {true, false se} (often write as {+ {+r, r, -r} r} ) meteor 0.0 • T in {h {hot, cold} [0, ¥ ) • D in [0 • L in possible locations, maybe {(0,0), (0,1), …} …}
Probability Distributions Joint Distributions • A • Unobse A joint dist stribution ove ver a se set of random va variables: s: serve ved random va variables s have ve dist stributions Shorthand notation: specifies sp s a real number for each assi ssignment (or out outcom come): ): T P W P hot 0.5 sun 0.6 cold 0.5 rain 0.1 T W P fog 0.3 hot sun 0.4 • Must obey: meteor 0.0 hot rain 0.1 OK if all domain entries are unique • Think k of a dist stribution as s a ta tabl ble of of pr proba babi biliti ties cold sun 0.2 cold rain 0.3 • Think k of probability y (lower case se va value) as s a si single entry y in this s table An Answer: d n • Size ze of dist stribution of of n n va variables s with domain si size zes s d? • Must • For all but the smallest distributions, impractical to write out! st have ve: and Probabilistic Models Events • Distribution over T, W A A probabilist stic model is s a joint dist stribution ove ver a • An An eve vent is s a se set E of of out outcomes comes se set of random va variables T W P hot sun 0.4 • Probabilist stic models: s: hot rain 0.1 • Random Random va variables s with domains • From a joint dist stribution, we can • cold sun 0.2 Assignments are called outcom outcomes es cal calcul culat ate e th the probability y of any y eve vent • Jo Joint dist stributions: s: say whether assignments cold rain 0.3 T W P (outcomes) are likely hot sun 0.4 • Normalize zed: sum to 1.0 Constraint over T, W • Probability that it’s hot AND su sunny ? • hot rain 0.1 Ideally: y: only certain variables directly interact • Probability that it’s hot hot ? T W P cold sun 0.2 • Probability that it’s hot OR su sunny ? hot sun T • Const straint sa satisf sfaction problems: s: cold rain 0.3 hot rain F • Variables s with domains • Typ ypically, y, the eve vents s we care about are cold sun F • Const straints: s: state whether assignments are possible partial assi ssignments, like ke P( P(T=h =hot) • Ideally: y: only certain variables directly interact cold rain T
Quiz: Events Marginal Distributions • P(+x, 0. 0.2 x, +y) y) ? • Marginal dist stributions ar are e “su sub-tables” s” which eliminate va variables s • Marginaliza zation (su summing out): Combine collapse sed rows s by y adding X Y P +x +y 0.2 • P(+x) 0. 0.5 x) ? T P +x -y 0.3 hot 0.5 -x +y 0.4 T W P cold 0.5 -x -y 0.1 hot sun 0.4 • P( 0. 0.6 P(-y y OR +x) x) ? hot rain 0.1 cold sun 0.2 W P cold rain 0.3 sun 0.6 rain 0.4 Quiz: Marginal Distributions Conditional Probabilities • A si simple relation between jo join int and and cond conditional onal prob obab abilities es • In fact, this is taken as the de definition of a cond conditional onal prob obab ability X P +x 0.5 P(a,b) X Y P -x 0.5 +x +y 0.2 +x -y 0.3 -x +y 0.4 Y P P(a) P(b) -x -y 0.1 +y 0.6 -y 0.4 T W P hot sun 0.4 hot rain 0.1 cold sun 0.2 cold rain 0.3
Quiz: Conditional Probabilities Conditional Distributions • P(+x 0.2 / (0 0. (0.2 + 0. 0.4) 4) = 0. 0.33 x | +y) y) ? • Conditional dist stributions are probability y dist stributions s ove ver so some va variables s give ven fixe xed va values s of others Conditional Distributions X Y P Joint Distribution • P( 0. 0.4 4 / (0 (0.2 + 0. 0.4) 4) = 0. 0.66 66 = = 1- 0. 0.33 33 +x +y 0.2 P(-x x | +y) y) ? +x -y 0.3 W P T W P -x +y 0.4 sun 0.8 hot sun 0.4 -x -y 0.1 rain 0.2 hot rain 0.1 • P( 0. 0.3 3 / (0 (0.2 + 0. 0.3) 3) = 0. 0.6 P(-y y | +x) x) ? cold sun 0.2 cold rain 0.3 W P sun 0.4 rain 0.6 Normalization Trick Normalization Trick NORMALIZE the selection SELECT the joint (make it sum to one) T W P probabilities T W P matching the hot sun 0.4 W P hot sun 0.4 evidence W P T W P hot rain 0.1 sun 0.4 hot rain 0.1 sun 0.4 cold sun 0.2 cold sun 0.2 rain 0.6 cold sun 0.2 rain 0.6 cold rain 0.3 cold rain 0.3 cold rain 0.3
Normalization Trick Quiz: Normalization Trick • P( P(X X | Y= Y=-y) y) ? NORMALIZE the selection SELECT the joint (make it sum to one) probabilities SELECT the joint NORMALIZE the selection T W P matching the (make it sum to one) probabilities evidence hot sun 0.4 X Y P W P T W P matching the X Y P X Y P hot rain 0.1 +x +y 0.2 evidence sun 0.4 cold sun 0.2 +x -y 0.75 +x -y 0.3 cold sun 0.2 +x -y 0.3 rain 0.6 cold rain 0.3 -x -y 0.25 -x -y 0.1 cold rain 0.3 -x +y 0.4 -x -y 0.1 • Why does this work? Sum of selection is P(evi vidence) ! (here P(T (T=c) ) To Normalize Probabilistic Inference • (Dictionary) y) To bring or rest store to a nor normal al cond condition on • Probabilist stic inference: compute a desired probability from other known probabilities (e.g. conditional from joint) All entries sum to ONE • Pr Procedu dure: • We generally y compute conditional probabilities s • St Step p 1: Compute Z = su sum ove ver all entries • P(on time | no reported accidents) • St s) = 0.90 Step p 2: Divide every entry by Z • These represent the agent’s beliefs s given the evi vidence Ex Examp mple 2 Examp Ex mple 1 • Probabilities s change with new evi vidence: T W P T W P W P W P Normalize • P(on time | no accidents, s, 5 a.m.) = 0.95 hot sun 20 Normalize hot sun 0.4 sun 0.2 sun 0.4 • P(on time | no accidents, s, 5 a.m., raining) = 0.80 hot rain 5 hot rain 0.1 rain 0.3 Z = 0.5 rain 0.6 • Additional evidence causes beliefs Z = 50 s to be updated cold sun 10 cold sun 0.2 cold rain 0.3 cold rain 15
Recommend
More recommend