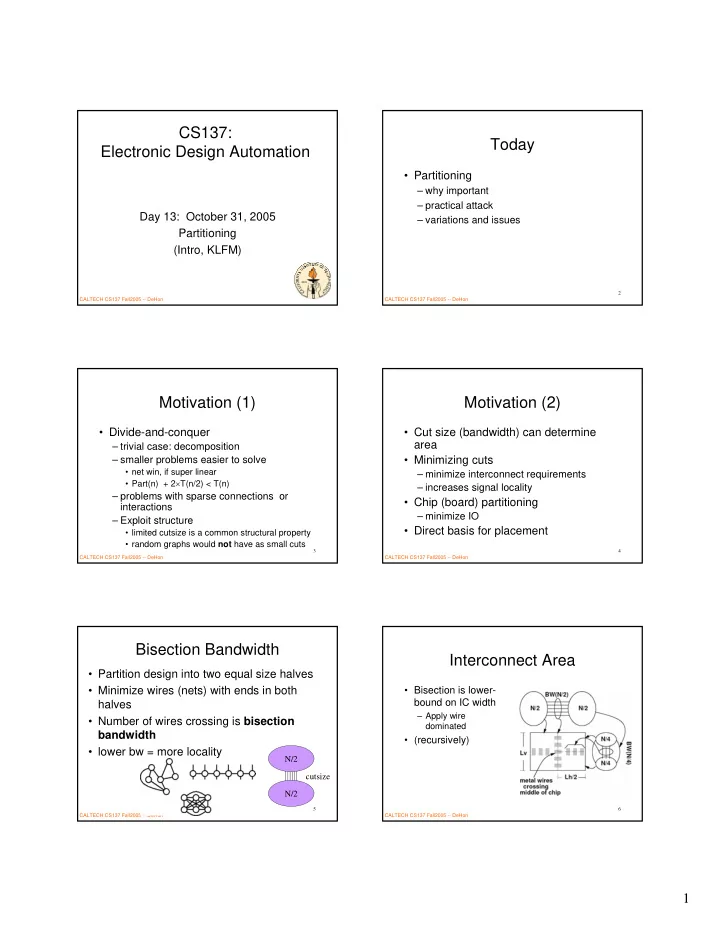

CS137: Today Electronic Design Automation • Partitioning – why important – practical attack Day 13: October 31, 2005 – variations and issues Partitioning (Intro, KLFM) 1 2 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Motivation (1) Motivation (2) • Divide-and-conquer • Cut size (bandwidth) can determine area – trivial case: decomposition • Minimizing cuts – smaller problems easier to solve • net win, if super linear – minimize interconnect requirements • Part(n) + 2 × T(n/2) < T(n) – increases signal locality – problems with sparse connections or • Chip (board) partitioning interactions – minimize IO – Exploit structure • Direct basis for placement • limited cutsize is a common structural property • random graphs would not have as small cuts 3 4 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Bisection Bandwidth Interconnect Area • Partition design into two equal size halves • Minimize wires (nets) with ends in both • Bisection is lower- bound on IC width halves – Apply wire • Number of wires crossing is bisection dominated bandwidth • (recursively) • lower bw = more locality N/2 cutsize N/2 5 6 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 1
Classic Partitioning Problem Balanced Partitioning • Given: netlist of interconnect cells • NP-complete for general graphs – [ND17: Minimum Cut into Bounded Sets, • Partition into two (roughly) equal halves Garey and Johnson] (A,B) – Reduce SIMPLE MAX CUT • minimize the number of nets shared by – Reduce MAXIMUM 2-SAT to SMC halves – Unbalanced partitioning poly time • “Roughly Equal” • Many heuristics/attacks – balance condition: (0.5- δ )N ≤ |A| ≤ (0.5+ δ )N 7 8 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Fiduccia-Mattheyses (Kernighan-Lin refinement) KL FM Partitioning Heuristic • Start with two halves (random split?) • Greedy, iterative • Repeat until no updates – pick cell that decreases cut and move it – Start with all cells free – repeat – Repeat until no cells free • small amount of non-greediness: • Move cell with largest gain (balance allows) • Update costs of neighbors – look past moves that make locally worse • Lock cell in place (record current cost) – randomization – Pick least cost point in previous sequence and use as next starting position • Repeat for different random starting points 9 10 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Efficiency Ordering and Cheap Update Tricks to make efficient: • Keep track of Net gain on node == delta net crossings to move a node • Expend little (O(1)) work picking move � cut cost after move = cost - gain candidate • Calculate node gain as Σ net gains for • Update costs on move cheaply [O(1)] all nets at that node • Efficient data structure – Each node involved in several nets – update costs cheap • Sort by gain A – cheap to find next move C B 11 12 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 2
FM Cell Gains FM Cell Gains Gain = Delta in number of nets crossing between partitions Gain = Delta in number of nets crossing between partitions = Sum of net deltas for nets on the node = Sum of net deltas for nets on the node 0 -4 1 +4 2 0 13 14 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Composability of Net Gains After move node? • Update cost each -1 – Newcost=cost-gain -1 -1+1-0-1 = -1 • Also need to update gains – on all nets attached to moved node – but moves are nodes, so push to 0 -1 +1 • all nodes affected by those nets 15 16 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Recompute Cell Gain FM Recompute Cell Gain • For each net, keep track of number of cells in • For each net, keep track of number of cells in each partition [F(net), T(net)] each partition [F(net), T(net)] • Move update:(for each net on moved cell) • Move update:(for each net on moved cell) – if T(net)==0, increment gain on F side of net – if T(net)==0, increment gain on F side of net • (think -1 => 0) • (think -1 => 0) – if T(net)==1, decrement gain on T side of net • (think 1=>0) 17 18 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 3
FM Recompute Cell Gain FM Recompute Cell Gain • Move update:(for each net on moved cell) • Move update:(for each net on moved cell) – if T(net)==0, increment gain on F side of net – if T(net)==0, increment gain on F side of net – if T(net)==1, decrement gain on T side of net – if T(net)==1, decrement gain on T side of net – decrement F(net), increment T(net) – decrement F(net), increment T(net) – if F(net)==1, increment gain on F cell 19 20 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Recompute Cell Gain FM Recompute Cell Gain • Move update:(for each net on moved cell) • For each net, keep track of number of cells in – if T(net)==0, increment gain on F side of net each partition [F(net), T(net)] – if T(net)==1, decrement gain on T side of net • Move update:(for each net on moved cell) – decrement F(net), increment T(net) – if T(net)==0, increment gain on F side of net – if F(net)==1, increment gain on F cell • (think -1 => 0) – if F(net)==0, decrement gain on all cells (T) – if T(net)==1, decrement gain on T side of net • (think 1=>0) – decrement F(net), increment T(net) – if F(net)==1, increment gain on F cell – if F(net)==0, decrement gain on all cells (T) 21 22 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Recompute (example) FM Recompute (example) +1 +1 +1 +1 [note markings here [note markings here are deltas…earlier are deltas…earlier pix were absolutes] pix were absolutes] 23 24 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 4
FM Recompute (example) FM Recompute (example) +1 +1 +1 +1 +1 +1 +1 +1 0 0 0 -1 0 0 0 -1 0 0 0 0 [note markings here [note markings here are deltas…earlier are deltas…earlier pix were absolutes] pix were absolutes] 25 26 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Recompute (example) FM Recompute (example) +1 +1 +1 +1 +1 +1 +1 +1 0 0 0 -1 0 0 0 -1 0 0 0 0 0 0 0 0 +1 0 0 0 +1 0 0 0 -1 -1 -1 -1 [note markings here [note markings here are deltas…earlier are deltas…earlier pix were absolutes] pix were absolutes] 27 28 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Data Structures FM Optimization Sequence (ex) • Partition Counts A,B • Cells • Two gain arrays – successors – One per partition (consumers) – Key: constant time – inputs cell update – locked status Binned by cost � constant time update 29 30 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 5
FM Running Time? FM Running Time • Randomly partition into two halves • Claim: small number of passes (constant?) to • Repeat until no updates converge • Small (constant?) number of random starts – Start with all cells free • N cell updates each round (swap) – Repeat until no cells free • Updates K + fanout work (avg. fanout K) • Move cell with largest gain – assume K-LUTs • Update costs of neighbors • Maintain ordered list O(1) per move • Lock cell in place (record current cost) – every io move up/down by 1 – Pick least cost point in previous sequence and • Running time: O(KN) use as next starting position – Algorithm significant for its speed (more than • Repeat for different random starting points quality) 31 32 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon FM Starts? Weaknesses? • Local, incremental moves only – hard to move clusters So, FM gives – no lookahead a not bad solution quickly • Looks only at local structure 21K random starts, 3K network -- Alpert/Kahng 33 34 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon Improving FM Clustering • Group together several leaf cells into • Clustering cluster • Technology mapping • Run partition on clusters • Initial partitions • Uncluster (keep partitions) • Runs – iteratively • Partition size freedom • Run partition again • Replication – using prior result as starting point • instead of random start Following comparisons from Hauck and Boriello ‘96 35 36 CALTECH CS137 Fall2005 -- DeHon CALTECH CS137 Fall2005 -- DeHon 6
Recommend
More recommend