Course Info MA13 - Multivariable Calculus Fall 2009 Meeting Times - PowerPoint PPT Presentation

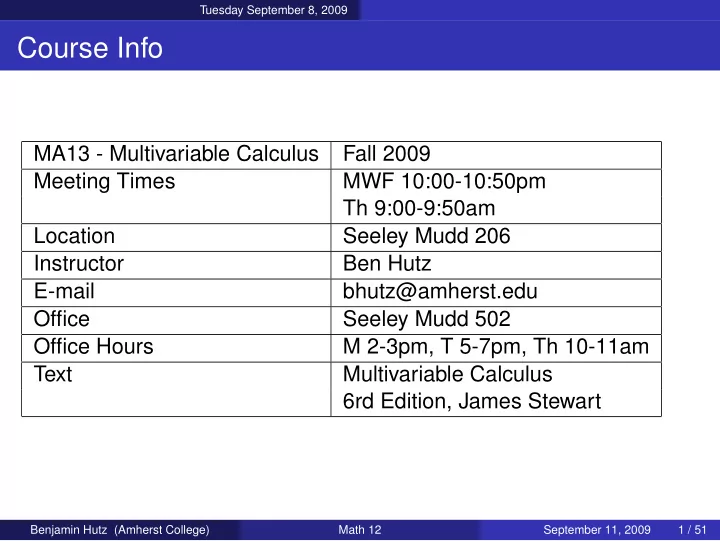
Tuesday September 8, 2009 Course Info MA13 - Multivariable Calculus Fall 2009 Meeting Times MWF 10:00-10:50pm Th 9:00-9:50am Location Seeley Mudd 206 Instructor Ben Hutz E-mail bhutz@amherst.edu Office Seeley Mudd 502 Office Hours M 2-3pm, T 5-7pm, Th 10-11am Text Multivariable Calculus 6rd Edition, James Stewart Benjamin Hutz (Amherst College) Math 12 September 11, 2009 1 / 51

Tuesday September 8, 2009 Overview/Evaluation Elementary vector calculus; introduction to partial derivatives; extrema of functions of several variables; multiple integrals in two and three dimensions; line integrals in the plane; Green’s theorem. 5% Group Projects 15% Homework 50% Three in-class exams 30% Final Exam Benjamin Hutz (Amherst College) Math 12 September 11, 2009 2 / 51

Tuesday September 8, 2009 Curving Grades: Final grades from a previous course Benjamin Hutz (Amherst College) Math 12 September 11, 2009 3 / 51

Tuesday September 8, 2009 Getting Help The Moss Quantitative Center provides math help. It is located in 202 Merrill Science Center and you can find the math hours at http://www.amherst.edu/˜qcenter/ . The Dean of Students Office can arrange for peer tutoring. Information can be found at http://www.amherst.edu/˜dos/acadsupport.html . Please come see me during my office hours! If you have a conflict and cannot make my office hours, please email me and we can set up an appointment for another time. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 4 / 51

Tuesday September 8, 2009 Three Dimensions What separates multivariable from single variable calculus is the addition of a third dimension. You have a 3-dimensional coordinate axes labeled x , y , z which are broken up into 8 octants 3 coordinate planes In 2-dim you have points 1 lines 2 Two distinct lines either intersect in a point or are parallel. In 3dim you have points 1 lines 2 planes 3 Two distinct planes either intersect in a line or are parallel. Two distinct lines intersect in a point, are parallel, or are skew. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 5 / 51

Tuesday September 8, 2009 The distance between two points You can have distance formula formula � ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 | P 1 P 2 | = Benjamin Hutz (Amherst College) Math 12 September 11, 2009 6 / 51

Tuesday September 8, 2009 The distance between two points You can have distance formula formula � ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 | P 1 P 2 | = Proof. Rectangular box with P 1 and P 2 in opposite corners and label the in-between corners as A , B . So you have from Pythagorean Theorem that | P 1 P 2 | 2 = | P 1 B | 2 + | P 2 B | 2 | P 1 B | 2 = | P 1 A | 2 + | AB | 2 Combining these we get | P 1 P 2 | 2 = | P 1 A | 2 + | AB | 2 + | P 2 B | 2 = | x 2 − x 1 | 2 + | y 2 − y 1 | 2 + | z 2 − z 1 | 2 Benjamin Hutz (Amherst College) Math 12 September 11, 2009 6 / 51

Tuesday September 8, 2009 A problem Problem Find an equation for describing the set of all points equidistant from ( − 1 , 2 , 3 ) and ( 3 , 0 , − 1 ) . (What common geometric object is the set?) Benjamin Hutz (Amherst College) Math 12 September 11, 2009 7 / 51

Tuesday September 8, 2009 A problem Problem Find an equation for describing the set of all points equidistant from ( − 1 , 2 , 3 ) and ( 3 , 0 , − 1 ) . (What common geometric object is the set?) Proof. We need � � ( x + 1 ) 2 + ( y − 2 ) 2 + ( z − 3 ) 2 = ( x − 3 ) 2 + y 2 + ( z + 1 ) 2 which is 2 x − y − 2 z + 1 = 0 . This is a plane. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 7 / 51

Tuesday September 8, 2009 Another example Problem Find an equation of the sphere with center ( 2 , − 6 , 4 ) and radius 5. Describe its intersection with each of the coordinate planes. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 8 / 51

Tuesday September 8, 2009 Another example Problem Find an equation of the sphere with center ( 2 , − 6 , 4 ) and radius 5. Describe its intersection with each of the coordinate planes. Proof. The equation is ( x − 2 ) 2 + ( y + 6 ) 2 + ( z − 4 ) 2 = 25. The intersection with the xy -plane( z = 0) is ( x − 2 ) 2 + ( y + 6 ) 2 = 9 a circle of radius 3 centered at ( 2 , − 6 ) . The intersection with the xz -plane ( y = 0 is ( x − 2 ) 2 + ( z − 4 ) 2 = − 9. In other words, there intersection is empty. The intersection with the yz -plane( x = 0) is ( y + 6 ) 2 + ( z − 4 ) 4 = 21. √ 21 centered at ( − 6 , 4 ) . In other words, a circle of radius Benjamin Hutz (Amherst College) Math 12 September 11, 2009 8 / 51

Tuesday September 8, 2009 Vectors Definition A vector has both a magnitude a direction. A scalar has only a magnitude. For example, 20mph is a scalar, but 20mph due east is a vector. Some Terminology: Initial Point Terminal Point Components Magnitude or length We will denote a vector as − → a = � a 1 , a 2 , a 3 � where a 1 is the number of units to move in the x direction, etc. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 9 / 51

Tuesday September 8, 2009 Magnitude and Unit vectors Definition The magnitude of a vector − → a is the distance from its initial point to its terminal point and is denoted | a | . (The initial point is assumed to be the origin unless otherwise specified). Example √ 3 3 + 4 2 = 5. |� 3 , 4 �| = Definition A unit vector is a vector with magnitude 1 and is generally thought of as a “direction”. Example 1 3 � 1 , 1 , 1 � . √ Benjamin Hutz (Amherst College) Math 12 September 11, 2009 10 / 51

Tuesday September 8, 2009 Parallel in 3-dimensions Problem How do we tell if two lines are parallel? Benjamin Hutz (Amherst College) Math 12 September 11, 2009 11 / 51

Tuesday September 8, 2009 Parallel in 3-dimensions Problem How do we tell if two lines are parallel? Proof. In two dimensions we have y = mx + b . If m 1 = m 2 then they are parallel, in other words if � m 1 , 1 � = c � m 2 , 1 � for some constant c . Then we can easily generalize to 3-dimensions with vectors: two lines are parallel if their direction vectors are equal up to scaling. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 11 / 51

Tuesday September 8, 2009 Vector Addition and Scalar Multiplication Addition of vectors � a 1 , a 2 � + � b 1 , b 2 � = � a 1 + b 1 , a 2 + b 2 � . (triangle and parallelogram laws(commutativity)) scalar multiplication c � a 1 , a 2 � = � ca 1 , ca 2 � . There are at least two ways to define vector multiplication (dot product, cross product) which we will discuss later. Benjamin Hutz (Amherst College) Math 12 September 11, 2009 12 / 51

Tuesday September 8, 2009 Alternate Notation We define ˆ ˆ ˆ i = � 1 , 0 , 0 � j = � 0 , 1 , 0 � k = � 0 , 0 , 1 � and so we can write � a 1 , a 2 , a 3 � = a 1 ˆ i + a 2 ˆ j + a 3 ˆ k . Benjamin Hutz (Amherst College) Math 12 September 11, 2009 13 / 51

Tuesday September 8, 2009 Position and Displacement Vectors Definition Given a point P = ( P 1 , P 2 , P 3 ) its displacement vector is the vector with initial point the origin and terminal point P and is denoted − → P . Definition The displacement vector from P to Q is the vector PQ = − − → → Q − − → P and is not the same as − → QP . Benjamin Hutz (Amherst College) Math 12 September 11, 2009 14 / 51

Wednesday September 9, 2009 Dot Product Definition a · � � b = a 1 b 1 + a 2 b 2 + a 3 b 3 Example � 1 , 2 , 3 � · �− 1 , 0 , 5 � = − 1 + 0 + 15 = 14. Notice two things the result is a scalar. 1 it is possible to get 0 without one of the vectors being � 0. 2 Benjamin Hutz (Amherst College) Math 12 September 11, 2009 15 / 51

Wednesday September 9, 2009 Properties Proposition The dot product satisfies the following properties. a · � b = � commutative � b · � a 1 � 2 � a · � � � � � a = a 2 a · � a · c � a · � c � b = � b = c ( � b ) 3 � � a · � � � � � � � � b = a b � cos θ 4 � � � Benjamin Hutz (Amherst College) Math 12 September 11, 2009 16 / 51

Wednesday September 9, 2009 Properties Proposition The dot product satisfies the following properties. a · � b = � commutative � b · � a 1 � 2 a · � � � � � � a = a 2 a · � a · c � a · � c � b = � b = c ( � b ) 3 � � a · � � � � � � � � b = a b � cos θ 4 � � � Proof. a 1 b 1 + a 2 b 2 + a 3 b 3 = b 1 a 1 + b 2 a 2 + b 3 a 3 . 1 � 3 ) 2 = � 2 . a = a 2 1 + a 2 2 + a 2 2 + a 3 � � a · � � a 2 1 + a 2 � � 3 = ( a 2 Benjamin Hutz (Amherst College) Math 12 September 11, 2009 16 / 51

Wednesday September 9, 2009 Proof Continued Proof. 3 a · � c � b = � ca 1 , ca 2 � · � b 1 , b 2 � = ca 1 b 1 + ca 2 b 2 a · c � = a 1 cb 1 + a 2 cb 2 = � b a · � = ca 1 b 1 + ca 2 b 2 = c ( a 1 b 1 + a 2 b 2 ) = c ( � b ) Benjamin Hutz (Amherst College) Math 12 September 11, 2009 17 / 51