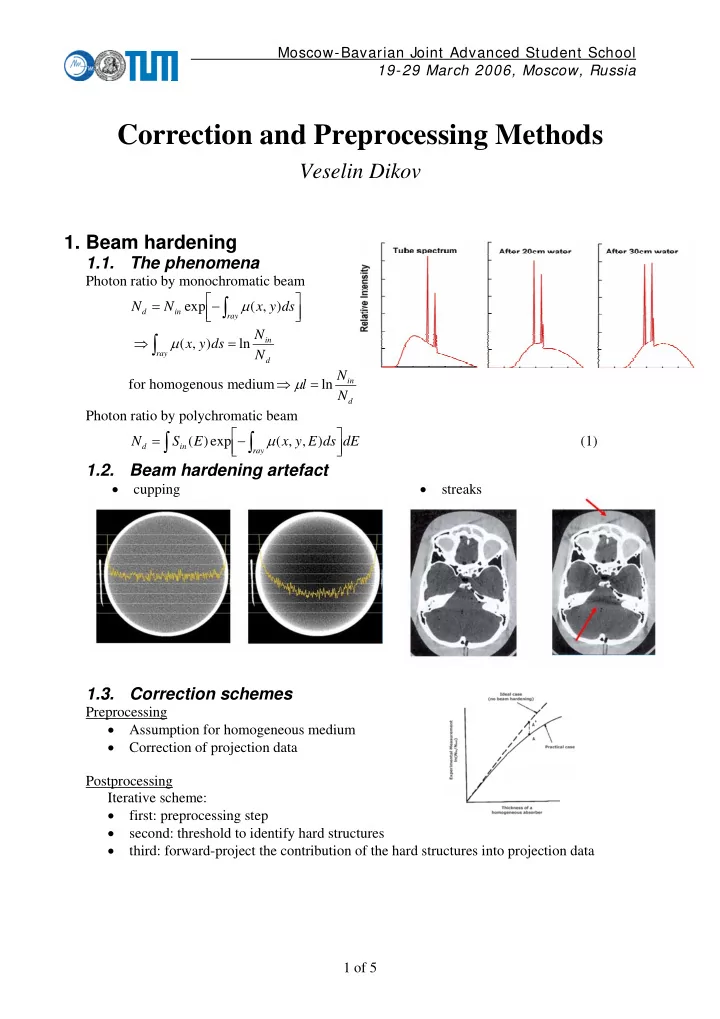

Moscow-Bavarian Joint Advanced Student School 19-29 March 2006, Moscow, Russia Correction and Preprocessing Methods Veselin Dikov 1. Beam hardening 1.1. The phenomena Photon ratio by monochromatic beam ⎡− ⎤ ∫ = μ N N exp ( x , y ) ds ⎢ ⎥ ⎣ ⎦ d in ray ⇒ ∫ N μ = in ( x , y ) ds ln N ray d N ⇒ μ = in for homogenous medium l ln N d Photon ratio by polychromatic beam ⎡− ⎤ ∫ ∫ = μ ( ) exp ( , , ) (1) N S E x y E ds dE ⎢ ⎥ ⎣ ⎦ d in ray 1.2. Beam hardening artefact • cupping • streaks 1.3. Correction schemes Preprocessing • Assumption for homogeneous medium • Correction of projection data Postprocessing Iterative scheme: • first: preprocessing step • second: threshold to identify hard structures • third: forward-project the contribution of the hard structures into projection data 1 of 5
Moscow-Bavarian Joint Advanced Student School 19-29 March 2006, Moscow, Russia Dual-energy μ = + Substitute ( x , y , E ) a ( x , y ) g ( E ) a ( x , y ) f ( E ) in (1) 1 2 KN [ ] ∫ ⇒ = − + N S ( E ) exp ( A g ( E ) A f ( E )) dE d in 1 2 KN (2) ∫ = = where , for A a ( x , y ) ds i 1 , 2 i i ray Two scans with different voltage (different energy curves) [ ] ∫ = − + I ( A , A ) S ( E ) exp ( A g ( E ) A f ( E )) dE 1 1 2 1 1 2 KN [ ] ∫ = − + I ( A , A ) S ( E ) exp ( A g ( E ) A f ( E )) dE 2 1 2 2 1 2 KN ⇒ μ Reconstruct a ( x , y ) and a ( x , y ) now ( x , y , E ) can be reconstructed for any 1 2 energy 2. Scattered radiation Scattered radiation is a radiation that is deflected in the scanned medium. 2.1. Scatter-to-Primary Ratio (SPR) Broad beam model estimation for SPR ( ) ⎛ ⎞ s ⎜ ⎟ = μ st β + − + − 2 2 2 SPR 2 L L R L R 1 ⎜ ⎟ + ⎝ ⎠ 2 2 R s μ - scattering attenuation coefficient st β - fraction of scattered photons which are scattered forward 2.2. Scatter artefacts Loss of contrast = μ − μ Contrast without scatter: C ( ) t - linearly depends on b b material thickness + 1 SPR = Contrast with scatter: - no linear C ln − μ − μ + ( ) e SPR b dependence 2 of 5
Moscow-Bavarian Joint Advanced Student School 19-29 March 2006, Moscow, Russia Loss of sharpness Transmitted radiation: = + = ⋅ ∗ ∗ , where I I I I SPR I h t p sr sr p sr h - blurring kernel due to scattered radiation sr ∗ - 2D convolution 1 ∗ Detected radiation: = − ρ ) + ρ ∗ ∗ ⇒ I ( 1 I I h d t t vg = − ρ + ⋅ ∗ ∗ + ρ + ⋅ ∗ ∗ ∗ ∗ I ( 1 )( I SPR I h ) ( I SPR I h ) h d p p sr p p sr vg h - blurring kernel due to veiling glare vg ρ - fraction of veiling 2.3. Scatter Reduction Approaches • Anti-scatter grid • Air gaps • Beam collimation 2.4. Scatter Measurement • Opaque discs techniques • Aperture techniques • Hybrid techniques 2.5. Scatter Correction Schemes Convolution filtering Filter the smooth scatter signal from the image = + = + ⋅ ∗ ∗ I I I I SPR I h d p s p p s ⇒ = − ⋅ ∗ ∗ I I SPR I h p d p s Use I as an estimation for I , W - ratio of scatter signal to the total signal d p = − ∗ ∗ I I W ( I h ) p d d s Low-pass filtered version of the detected signal. Has to be filtered out ∞ ∞ ∫ ∫ ∗ ∗ = − − 1 2D convolution - ( g h )( x , y ) g ( u , v ) h ( x u , y v ) dudv − ∞ − ∞ 3 of 5
Moscow-Bavarian Joint Advanced Student School 19-29 March 2006, Moscow, Russia Scatter sampling schemes • Estimate scatter in sample points o Opaque disc arrays o Aperture arrays • Interpolate “scatter surface” (it is a smooth one) o 2D least squares fitting o Filtration with sinc and jinc o 2D polynomial fitting o 2D bicubic splines • Subtract the “scatter surface” estimation from the image 3. Ring artefacts Artefacts in the reconstructed image due to defect detector units; relevant for thirds generation CT ; only postprocessing correction possible. ROI 3.1. Correction scheme 1. Select Region of Interest (ROI). No data out of it is considered 2. Translate image to polar coordinates 3. Construct artefact pattern by doing search in window (red window on the image in right) Artefact pattern 4. Subtract the pattern from the image 5. Translate image back to Cartesian coordinages Search window 4 of 5
Moscow-Bavarian Joint Advanced Student School 19-29 March 2006, Moscow, Russia 4. References • T.Buzug, Einfürung in die Computertomographie, Springer-Verlag (2004) • A.Kak and M.Slaney, Principles of Computerized Tomographic Imaging, IEEE Press (1988) • K.P.Maher and J.F. Malone, Computerized scatter correction in diagnostic radiology, Contemporary Physics 38, 131-148 (1997). • J.Sijbers and A.Postnov, Reduction of ring artefacts in high resolution micro-CT reconstructions, Physics in Medicine and Biology Vol. 49 (07/2004) • M.Zellerhoff et al, Low contrast 3D-reconstruction from C-arm data, Medical Imaging SPIE, 646-655 (04/2004) 5 of 5
Recommend
More recommend