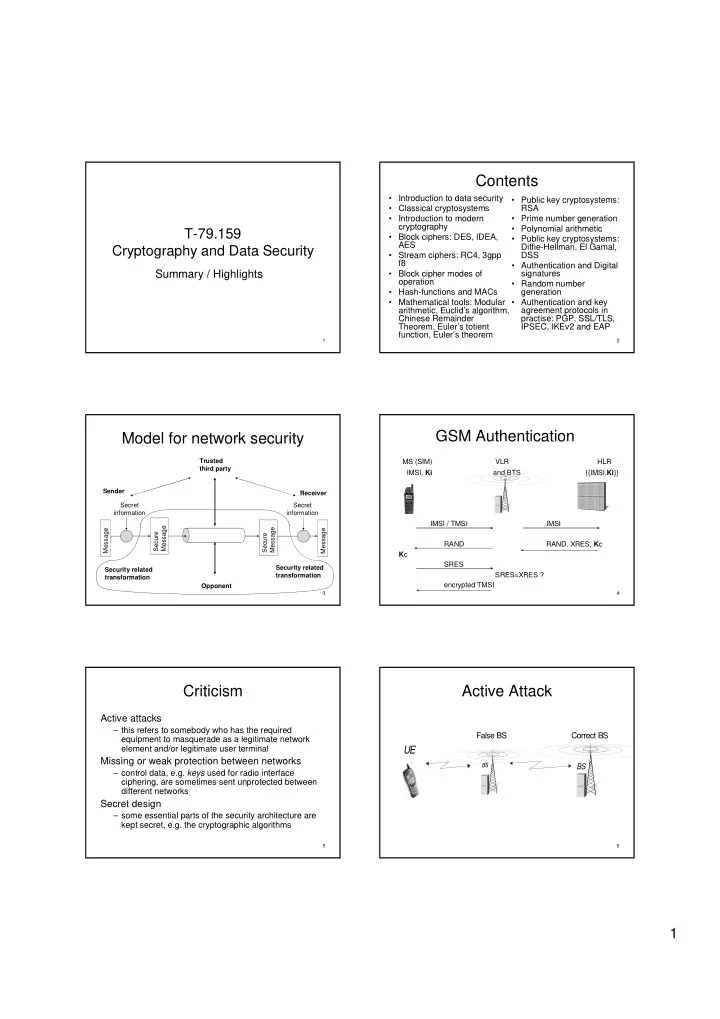
Contents Introduction to data security Public key cryptosystems: - PDF document

Contents • Introduction to data security • Public key cryptosystems: • Classical cryptosystems RSA • Introduction to modern • Prime number generation cryptography • Polynomial arithmetic T-79.159 • Block ciphers: DES, IDEA, • Public key cryptosystems: AES Diffie-Hellman, El Gamal, Cryptography and Data Security • Stream ciphers: RC4, 3gpp DSS f8 • Authentication and Digital Summary / Highlights • Block cipher modes of signatures operation • Random number • Hash-functions and MACs generation • Mathematical tools: Modular • Authentication and key arithmetic, Euclid’s algorithm, agreement protocols in Chinese Remainder practise: PGP, SSL/TLS, Theorem, Euler’s totient IPSEC, IKEv2 and EAP function, Euler’s theorem 1 2 GSM Authentication Model for network security Trusted MS (SIM) VLR HLR third party IMSI, Ki and BTS {{IMSI, Ki }} Sender Receiver Secret Secret information information IMSI / TMSI IMSI Message Message Message Message Secure Secure RAND RAND, XRES, K c K c SRES Security related Security related SRES=XRES ? transformation transformation encrypted TMSI Opponent 3 4 Criticism Active Attack Active attacks – this refers to somebody who has the required False BS Correct BS equipment to masquerade as a legitimate network element and/or legitimate user terminal UE Missing or weak protection between networks BS BS – control data, e.g. keys used for radio interface ciphering, are sometimes sent unprotected between different networks Secret design – some essential parts of the security architecture are kept secret, e.g. the cryptographic algorithms 5 6 1

Monoalphabetic substitution 2.1 Classical Cryptosystems Alphabets Ceasar Cipher, or Shift Cipher Plain: abcdefghijklmnopqrstuvwxyz Plain: meet me after the toga party Cipher: ABCDEFGHIJKLMNOPQRSTUVWXYZ Cipher: PHHW PH DIWHU WKH WRJD SDUWB Key = permutation of the 26 characters Size of key space 26! ≅ 4 x 10 26 Cryptanalysis based on statistical properties of the plaintext 7 8 Playfair Cipher Relative Frequency of Letters in English Text M O N A R N 6.749 A 8.167 O 7.507 B 1.492 C H Y B D P 1.929 C 2.782 E F G I/J K Q 0.095 D 4.253 R 5.987 L P Q S T E 12.702 S 6.327 F 2.228 U V W X Z T 9.056 G 2.015 U 2.758 H 6.094 The encryption rules V 0.978 I 6.996 W 2.360 J 0.153 Plaintext formatting Same row or column Regular case X 0.150 K 0.772 Y 1.974 oo -> oxo ar -> RM hs -> BP L 4.025 Z 0.074 M 2.406 mu -> CM ea -> IM 9 10 Kasiski’s method to determine the period Polyalphabetic ciphers: Vigenère • Many strings of characters repeat themselves in natural Plain and Cipher: languages. finite sequences of characters in {0,1,2,…,25} • Assume the interval between occurence of a string is a Key of period q : k 1 k 2 k 3 … k q-1 k q multiple of the period length. sequences of length q of characters in {0,1,2,…,25} • Then a repetition of a character string of the same length Encryption: occurs in the ciphertext. c 1 = (p 1 + k 1 )mod 26 c q+1 =(p q+1 + k 1 )mod 26 • By detecting repetitions of strings in the ciphertext one can find the period as the greatest common divisor (GCD) of the c 2 = (p 2 + k 2 )mod 26 c q+2 = (p q+2 + k 2 )mod 26 repetition intervals ... ... • Their may be false repetitions. The longer the repeating string c q = (p q + k q )mod 26 c 2q = (p 2q + k q )mod 26 the more significant it is. Repeating strings of length ≥ 3 are and so on.. the most significant. 11 12 2

Block ciphers, security One Time Pad • Security is measured in terms of time: How long it takes to break the cipher using available resources. • Claude Shannon laid (1949) the information theoretic fundamentals of secrecy systems. • Upperbound of security: The time complexity of exhaustive key search, which is equal to 2 k , with key • Shannon’s pessimistic inequality: For perfect secrecy length of k bits. you need as much key as you have plaintext. A second upperbound: 2 n/ 2 , with block length n (due to • • An example of a cipher which achieves perfect secrecy Birthday paradox, to be explained later) is the One Time Pad • If an attack leads to a break, in time 2 t , where t < k , c i = (p i + k i )mod 26 then the cipher is said to be theoretically broken, and where the key is a string of characters k 1 k 2 k 3 … k i that the effective key length of the cipher is reduced to chosen uniformly at random. t . (This does not mean that the cipher is broken in • Practical ciphers do not provide perfect secrecy practise unless t is very small.) 13 14 Block ciphers, design principles DES Data Encryption Standard 1977 - 2002 • The ultimate design goal of a block cipher is to use the • Standard for 25 years secret key as efficiently as possible. • Finally found to be too small. DES key is only 56 bits, that is, there • Confusion and diffusion (Shannon) are about 10 16 different keys. By manufacturing one million chips, such that, each chip can test one million keys in a second, then • New design criteria are being discovered as response one can find the key in about one minute. to new attacks. • The EFF DES Cracker built in 1998 can search for a key in about • A state-of-the-art block cipher is constructed taking 4,5 days. The cost of the machine is $250 000. into account all known attacks and design principles. • DES has greately contributed to the development of cryptologic • But no such block cipher can become provably secure, research on block ciphers. it may remain open to some new, unforeseen attacks. • The design was a joint effort by CIA and IBM. The design • Common constructions with iterated round function principles were not published until little-by-little. The complete set – Substitution permutation network (SPN) of design criteria is still unknown. – Feistel network • Differential cryptanalysis 1989 • Linear cryptanalysis 1993 15 16 The Security of IDEA One round of IDEA: odd round • IDEA has been around almost 15 years Xa (16 bits) Xb (16 bits) Xc (16 bits) Xd (16 bits) • Designed by Xuejia Lai and Jim Massey • Its only problem so far is its small block size Ka Kb Kc Kd • Numerous analysis has been published, but nothing substantial mult add add mult • It is not available in public domain, except for research purposes • It is available under licence • It is widely used, e.g in PGP (see Lecture 11) Xa (16 bits) Xb (16 bits) Xc (16 bits) Xd (16 bits) Legend: mult Multiplication modulo 2 16 +1, where input 0 is replaced by 2 16 , and result 2 16 is encoded as 0 Addition modulo 2 16 add 17 18 3

One round of IDEA: even round The mangler function Y out = (Ke mult Y in ) add Z in ) mult Kf Xa (16 bits) Xb (16 bits) Xc (16 bits) Xd (16 bits) Z out = (Ke mult Y in ) add Y out xor xor Y in Z in Ke Kf Ke Mangler mult add function Kf xor xor xor xor add mult Xa (16 bits) Xb (16 bits) Xc (16 bits) Xd (16 bits) Y out Z out 19 20 AES Rijndael - Internal Structure AES • First Initial Round Key Addition • Candidates due June 15, 1998: 21 submissions, 15 • 9 rounds, numbered 1-9, each consisting of met the criteria Byte Substitution transformation • 5 finalists August 1999: MARS, RC6, Rijndael, Shift Row transformation Serpent, and Twofish, (along with regrets for E2) Mix Column transformation • October 3, 2000, NIST announces the winner: Round Key Addition Rijndael • A final round (round 10) consisting of • FIPS 197, November 26, 2001 Byte Substitution transformation Federal Information Processing Standards Shift Row transformation Publication 197, ADVANCED ENCRYPTION STANDARD (AES) Final Round Key Addition 21 22 The Security of AES Stream ciphers • Stream ciphers are generally faster than block ciphers, especially when implemented in hardware. • Designed to be resistant against differential and • Stream ciphers have less hardware complexity. linear cryptanalysis • Stream ciphers can be adapted to process the plaintext bit by bit, or – S-boxes optimal word by word, while block ciphers require buffering to accumulate – Wide Trail Strategy the full plaintext block. • Has quite an amazing algebraic structure (see the • Synchronous stream ciphers have no error propagation; encryption next slide) is done character by character with keys K i that are independent of the data • Algebraic cryptanalysis tried but not yet (!) C i = E Ki (P i ) successful • Function E is simple, the function which computes the key • Algebraic cryptanalysis: given known plaintext – sequence is complex ciphertext pairs construct algebraic systems of • Example: Vigenère cipher, One Time Pad equations, and try to solve them. C i = ( P i + K i )mod 26 23 24 4