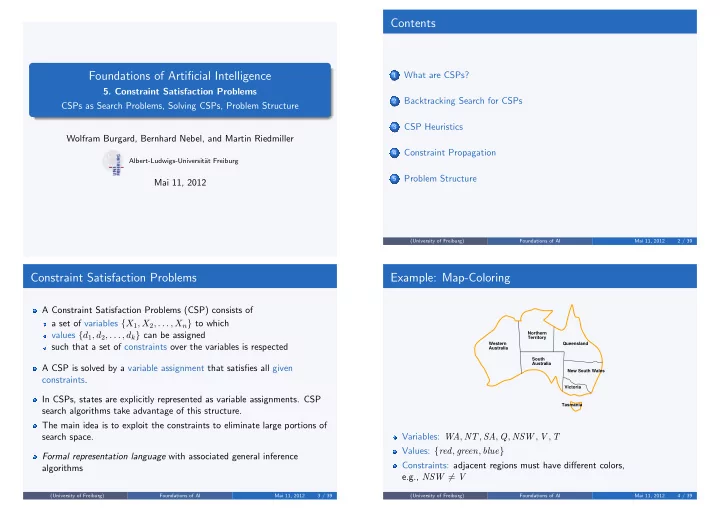
Contents Foundations of Artificial Intelligence What are CSPs? 1 5. Constraint Satisfaction Problems Backtracking Search for CSPs 2 CSPs as Search Problems, Solving CSPs, Problem Structure CSP Heuristics 3 Wolfram Burgard, Bernhard Nebel, and Martin Riedmiller Constraint Propagation 4 Albert-Ludwigs-Universit¨ at Freiburg Problem Structure 5 Mai 11, 2012 (University of Freiburg) Foundations of AI Mai 11, 2012 2 / 39 Constraint Satisfaction Problems Example: Map-Coloring A Constraint Satisfaction Problems (CSP) consists of a set of variables { X 1 , X 2 , . . . , X n } to which Northern values { d 1 , d 2 , . . . , d k } can be assigned Territory Western Queensland such that a set of constraints over the variables is respected Australia South Australia A CSP is solved by a variable assignment that satisfies all given New South Wales constraints. Victoria In CSPs, states are explicitly represented as variable assignments. CSP Tasmania search algorithms take advantage of this structure. The main idea is to exploit the constraints to eliminate large portions of Variables: WA , NT , SA , Q , NSW , V , T search space. Values: { red , green , blue } Formal representation language with associated general inference Constraints: adjacent regions must have different colors, algorithms e.g., NSW � = V (University of Freiburg) Foundations of AI Mai 11, 2012 3 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 4 / 39
Australian Capital Territory (ACT) One Solution and Canberra (inside NSW) Northern Territory Western Queensland Australia South Australia New South Wales Victoria Tasmania Solution assignment: { WA = red , NT = green , Q = red , NSW = green , V = red , SA = blue , T = green } View of the Australian National University and Telstra Tower Perhaps in addition ACT = blue (University of Freiburg) Foundations of AI Mai 11, 2012 5 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 6 / 39 Constraint Graph Variations NT Q WA Binary, ternary, or even higher arity (e.g., ALL DIFFERENT) SA NSW Finite domains ( d values) → d n possible variable assignments V Victoria Infinite domains (reals, integers) linear constraints : solvable (in P if real) T nonlinear constraints : unsolvable a constraint graph can be used to visualize binary constraints for higher order constraints, hyper-graph representations might be used Nodes = variables, arcs = constraints Note: Our problem is 3-colorability for a planar graph (University of Freiburg) Foundations of AI Mai 11, 2012 7 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 8 / 39
Applications Backtracking Search over Assignments Timetabling (classes, rooms, times) Configuration (hardware, cars, . . . ) Assign values to variables step by step (order does not matter) Spreadsheets Consider only one variable per search node! Scheduling DFS with single-variable assignments is called backtracking search Floor planning Frequency assignments Can solve n -queens for n ≈ 25 Sudoku . . . (University of Freiburg) Foundations of AI Mai 11, 2012 9 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 10 / 39 Algorithm Example (1) function B ACKTRACKING -S EARCH ( csp ) returns a solution, or failure return B ACKTRACK ( { } , csp ) function B ACKTRACK ( assignment , csp ) returns a solution, or failure if assignment is complete then return assignment var ← S ELECT -U NASSIGNED -V ARIABLE ( csp ) for each value in O RDER -D OMAIN -V ALUES ( var , assignment , csp ) do if value is consistent with assignment then add { var = value } to assignment inferences ← I NFERENCE ( csp , var , value ) if inferences � = failure then add inferences to assignment result ← B ACKTRACK ( assignment , csp ) if result � = failure then return result remove { var = value } and inferences from assignment return failure (University of Freiburg) Foundations of AI Mai 11, 2012 11 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 12 / 39
Example (2) Example (3) (University of Freiburg) Foundations of AI Mai 11, 2012 13 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 14 / 39 Example (4) Improving Efficiency: CSP Heuristics & Pruning Techniques Variable ordering: Which one to assign first? Value ordering: Which value to try first? Try to detect failures early on Try to exploit problem structure → Note: all this is not problem-specific! (University of Freiburg) Foundations of AI Mai 11, 2012 15 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 16 / 39
Variable Ordering: Variable Ordering: Most constrained first Most Constraining Variable First Break ties among variables with the same number of remaining legal Most constrained variable: values: choose the variable with the fewest remaining legal values choose variable with the most constraints on remaining unassigned → reduces branching factor! variables → reduces branching factor in the next steps (University of Freiburg) Foundations of AI Mai 11, 2012 17 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 18 / 39 Value Ordering: Rule out Failures early on: Least Constraining Value First Forward Checking Given a variable, choose first a value that rules out the fewest values in the remaining unassigned variables Whenever a value is assigned to a variable, values that are now illegal → We want to find an assignment that satisfies the constraints (of for other variables are removed course, does not help if unsat.) Implements what the ordering heuristics implicitly compute WA = red , then NT cannot become red Allows 1 value for SA If all values are removed for one variable, we can stop! Allows 0 values for SA (University of Freiburg) Foundations of AI Mai 11, 2012 19 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 20 / 39
Forward Checking (1) Forward Checking (2) Keep track of remaining values Keep track of remaining values Stop if all have been removed Stop if all have been removed WA NT Q NSW V SA T WA NT Q NSW V SA T (University of Freiburg) Foundations of AI Mai 11, 2012 21 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 22 / 39 Forward Checking (3) Forward Checking (4) Keep track of remaining values Keep track of remaining values Stop if all have been removed Stop if all have been removed WA NT Q NSW V SA T WA NT Q NSW V SA T (University of Freiburg) Foundations of AI Mai 11, 2012 23 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 24 / 39
Forward Checking: Arc Consistency Sometimes it Misses Something Forward Checking propagates information from assigned to unassigned A directed arc X → Y is “consistent” iff variables for every value x of X , there exists a value y of Y , such that ( x, y ) However, there is no propagation between unassigned variables satisfies the constraint between X and Y Remove values from the domain of X to enforce arc-consistency Arc consistency detects failures earlier Can be used as preprocessing technique or as a propagation step during WA NT Q NSW V SA T backtracking (University of Freiburg) Foundations of AI Mai 11, 2012 25 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 26 / 39 Arc Consistency Example AC3 Algorithm function AC-3( csp ) returns false if an inconsistency is found and true otherwise inputs : csp , a binary CSP with components ( X, D, C ) local variables : queue , a queue of arcs, initially all the arcs in csp while queue is not empty do ( X i , X j ) ← R EMOVE -F IRST ( queue ) if R EVISE ( csp , X i , X j ) then if size of D i = 0 then return false for each X k in X i .N EIGHBORS - { X j } do WA NT Q NSW V SA T add ( X k , X i ) to queue return true function R EVISE ( csp , X i , X j ) returns true iff we revise the domain of X i revised ← false for each x in D i do if no value y in D j allows ( x , y ) to satisfy the constraint between X i and X j then delete x from D i revised ← true return revised (University of Freiburg) Foundations of AI Mai 11, 2012 27 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 28 / 39
Properties of AC3 Problem Structure (1) NT Q WA AC3 runs in O ( d 3 n 2 ) time, with n being the number of nodes and d being the maximal number of elements in a domain SA NSW V Of course, AC3 does not detect all inconsistencies (which is an NP-hard Victoria problem) T CSP has two independent components Identifiable as connected components of constraint graph Can reduce the search space dramatically (University of Freiburg) Foundations of AI Mai 11, 2012 29 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 30 / 39 Problem Structure (2): Problem Structure (2): Tree-structured CSPs Tree-structured CSPs A E B D A B C D E F A E C F B D (a) (b) C F Pick any variable as root; choose an ordering such that each variable appears after its parent in the tree. If the CSP graph is a tree, then it can be solved in O ( nd 2 ) Apply arc-consistency to ( X i , X k ) , when X i is the parent of X k , for all k = n down to 2 . (any tree with n nodes has n − 1 arcs, per arc d 2 General CSPs need in the worst case O ( d n ) comparisons are needed: O ( n d 2 ) ) Idea: Pick root, order nodes, apply arc consistency from leaves to root, Now one can start at X 1 assigning values from the remaining domains and assign values starting at root without creating any conflict in one sweep through the tree! Algorithm linear in n (University of Freiburg) Foundations of AI Mai 11, 2012 31 / 39 (University of Freiburg) Foundations of AI Mai 11, 2012 32 / 39
Recommend
More recommend
