= condition condition dS v dS v Then S S - PowerPoint PPT Presentation

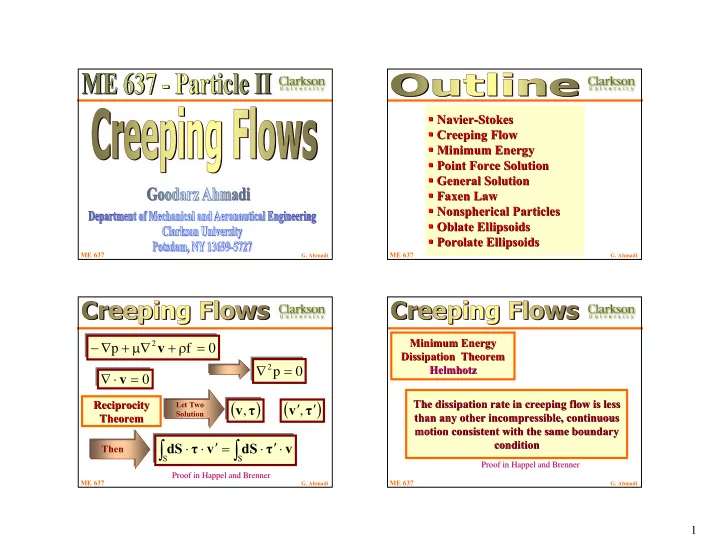
� Navier � Navier- -Stokes Stokes � Creeping Flow � Creeping Flow � Minimum Energy Minimum Energy � � Point Force Solution Point Force Solution � � General Solution General Solution � � Faxen � Faxen Law Law � Nonspherical � Nonspherical Particles Particles � Oblate Ellipsoids � Oblate Ellipsoids � Porolate � Porolate Ellipsoids Ellipsoids ME 637 ME 637 G. Ahmadi G. Ahmadi Minimum Energy Minimum Energy − ∇ + µ ∇ + ρ = 2 v p f 0 Dissipation Theorem Dissipation Theorem ∇ = 2 Helmhotz Helmhotz p 0 ∇ v ⋅ = 0 ( ) ( ) The dissipation rate in creeping flow is less The dissipation rate in creeping flow is less Reciprocity Reciprocity ′ , ′ Let Two Let Two v , τ v τ Solution Solution than any other incompressible, continuous than any other incompressible, continuous Theorem Theorem motion consistent with the same boundary motion consistent with the same boundary ∫ ∫ ′ ′ ⋅ ⋅ = ⋅ ⋅ condition condition dS τ v dS τ v Then S S Proof in Happel Proof in Happel and Brenner and Brenner Proof in Happel Happel and Brenner and Brenner Proof in ME 637 ME 637 G. Ahmadi G. Ahmadi 1

Minimum Energy Minimum Energy Stokes Stokes ( ) ij = = µ ∇ + δ δ 2 τ T i 0 P T , Dissipation Theorem Dissipation Theorem Equation j , i ij ij Equation [ ] ( ) ( ) ( ) ( ) ( ) ( ) ∫ ∫ ′ ′ ′ ′ ′ ′ = − ρ + τ − − − ⎡ ⎤ r r r r r r r r r r v T f dV T R v dS r r 1 = i ij jk ki ijk k j Solution- -3D 3D = δ + Solution i j P i V S T ⎢ ⎥ π i πµ 3 ij ij 4 r 2 8 r ⎣ r ⎦ 3 r r r ( ) = r i j k R π ijk 5 4 r ⎡ ⎤ r r 1 r Solution- Solution -2D 2D = − δ + = i j i T ln r P ⎢ ⎥ Then [ ] ij πµ ij i π ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 ⎣ ⎦ ∫ ∫ 4 r 2 r ′ ′ ′ ′ ′ ′ = − ρ + τ − + µ − r r r r r r r r r r p P f dV P 2 v P dS i i ij j j j , i i V S ME 637 ME 637 G. Ahmadi G. Ahmadi ( ) ∞ Lamb ( ) In an Unbounded Flow, In an Unbounded Flow, Lamb ρ = δ ∑ ( ) r = − − = + θ φ f F p P n n 1 P A r B r Y , n n n n nm For a point Force For a point Force i i = n 0 ∂ ⎛ ∂ ⎞ ∂ ⎛ ∂ ⎞ ∂ 2 1 1 1 ∇ = + θ + Stokeslet Stokeslet 2 ⎜ 2 ⎟ ⎜ ⎟ sin r ∂ ∂ θ ∂ θ ∂ θ θ ∂ ϕ 2 ⎝ ⎠ 2 ⎝ ⎠ 2 2 2 sin sin r r r r r ( ) F ⎡ + rr ⎤ i = v F T r ( ) ( ) ( ) = ⋅ θ φ = φ + φ θ v I m Y , C cos m D sin m P cos j ij ⎢ ⎥ mn mn mn n πµ ⎣ 2 ⎦ 8 r r n = m = 0 , 1 , 2 ,..., n 0 , 1 , 2 ,... ⋅ ( ) ( ) ( ) F r Then ∞ ⎡ + ∇ − ⎤ 2 r = ( ) ( ) n 3 r P 2 n P ∑ p r F P r = = ∇ × ξ + ∇ Φ + v r n n ⎢ ⎥ p ( )( ) n n µ + + i i ⎣ 2 n 1 2 n 3 ⎦ π = 3 n 0 4 r Spherical Harmonics Spherical Harmonics ME 637 ME 637 G. Ahmadi G. Ahmadi 2

Torque For nonuniform For nonuniform Torque Drag on an Drag on an U velocities velocities Axisymmetric Body Axisymmetric Body ⎛ ⎞ 1 = πµ ∇ × − T 0 3 ⎜ v ω ⎟ 8 R | ∞ [ ] o ⎝ ⎠ 2 = − + µ ( ) τ I d p 2 = ∇ + ∇ T d v v Force z Force ρ n ⎡ ⎤ 1 ( ) = πµ − + ∇ F v U 2 2 v ∫ 6 R | R | = ⋅ ⎢ ⎥ F dS τ ∞ ∞ o o ⎣ ⎦ 6 s S ⎛ ⎞ ( ) 2 ∫ 20 R = × ⋅ r dS τ = π µ ⎜ + ∇ ⎟ Stresslet Stresslet S d 3 2 T R 1 ⎜ ⎟ o 3 ⎝ 10 ⎠ S ME 637 ME 637 G. Ahmadi G. Ahmadi Drag on an ∫ ∫ Drag on an = ⋅ = ⋅ ⋅ = ⋅ ⋅ F e dS τ e n τ e F dS z ρ Flow for a Flow for a 2 F z F z z z z S S ψ = = − Axisymmetric Body Body Axisymmetric z p Point Force Point Force πµ 8 r π = πρ 3 dS 2 ds 4 r ψ = ρ + 2 2 2 r r z ∂ ∂ ∂ ∂ ⎛ ∂ ψ ⎞ µ ⎛ ⎞ ⎛ ⎞ v v v v 1 Point Point = πµ ⋅ = − + µ + + µ − = − − µ ∇ ⎜ ⎟ + ψ n τ n ⎜ n n s n ⎟ s ⎜ s n ⎟ n s 2 p 2 p 2 E F 8 lim ⎜ ⎟ ∂ ∂ ∂ ∂ ρ ∂ ρ ⎝ ⎠ ⎝ ⎠ Particle Particle n s n s ⎝ s ⎠ ρ z 2 → ∞ r ( ) ψ − ψ r ∂ ⎛ ψ ⎞ 2 Fluid not at Fluid not at E = πµ Drag Force ∞ Drag Force ∫ ⎜ ⎟ = µπ ρ F 8 lim 3 F dS ⎜ ⎟ ∂ ρ z 2 Z ρ n ⎝ ⎠ rest far away 2 rest far away → ∞ r ME 637 ME 637 G. Ahmadi G. Ahmadi 3

ψ = E 4 Boundary Conditions Boundary Conditions ⎧ = ξ θ φ ⎫ U 0 x c cosh sin cos ⎪ ⎪ = ξ θ φ ⎨ ⎬ y c cosh sin sin ⎪ ⎪ z = ξ θ ⎩ z c sinh cos ⎭ ( ) ξ = ξ o λ = λ ξ = ξ ψ = 0 0 0 λ = ξ a sinh ∞ > λ ≥ 0 b ∂ ψ Let Let ( ) = λ = λ ξ = ξ 0 ζ = θ cos ≥ ζ ≥ − 1 1 ∂ λ 0 0 ρ = + = ξ θ = λ + − ζ 2 2 2 2 x y c cosh sin c 1 1 ( )( ) 2 λ or ξ → ∞ 1 Uc ψ → ρ = λ + − ζ 2 2 2 U 1 1 2 2 = c λζ z ME 637 ME 637 G. Ahmadi G. Ahmadi ( ) ( ) Assumed Assumed ∂ ∂ ∂ ∂ ψ = − ζ λ 2 Boundary Conditions Boundary Conditions 1 g Noting = λ + = − − ζ Noting 2 2 Solution Solution 1 1 ∂ ξ ∂ λ ∂ θ ∂ ζ ( ) [ ( ) ] ( ) ⎟ ⎛ ⎞ 1 1 ψ = − ζ − λ + λ − λ + − λ + λ + ⎜ 2 2 1 2 1 C C 1 cot C 1 1 2 3 ∂ ∂ ∂ ⎝ ⎠ 2 2 2 2 1 = − + 2 E ∂ ρ ρ ∂ ρ ∂ 2 2 ( ) z ⎧ ⎫ ⎡ ⎤ λ λ − 2 1 − − λ 1 ⎪ ( ) ( 0 ) ⎪ ⎢ ⎥ cot Leads To Leads To λ + λ + ⎪ 2 2 ⎪ 1 1 1 ⎣ ⎦ Solution Solution ψ = ρ − 2 0 U ⎨ 1 ( ) ⎬ ⎡ ⎤ λ λ − 2 2 ⎪ 1 ⎪ − − λ 1 ( 0 ) ( 0 ) ⎡ ⎤ ⎢ ⎥ cot ) ( ) ∂ ( ) ∂ 2 2 1 ⎪ ⎪ λ + λ + 0 2 2 = λ + + − ζ 1 1 2 2 2 ⎩ ⎣ ⎦ ⎭ ( E 1 1 ⎢ ⎥ 0 0 λ + ζ ∂ λ ∂ ζ 2 2 2 2 2 c ⎣ ⎦ λ = sinh ξ 0 0 ME 637 ME 637 G. Ahmadi G. Ahmadi 4

( ) = − πµ Drag Drag λ ⎡ λ − ⎤ 2 F 6 aUK 1 Solution for Solution for − − λ 1 ( ) ( 0 ) ⎢ ⎥ cot Z λ + λ + Oblate Oblate 2 2 1 ⎣ 1 ⎦ 1 ψ = − ρ 2 0 ( ) U Spheroids Spheroids ⎡ ⎤ λ λ − 2 2 1 − moving in a moving in a − λ ( ) ( ) 1 0 0 cot ⎢ ⎥ 1 λ + λ + 0 2 2 stationary fluid stationary fluid 1 ⎣ 1 ⎦ = K 0 0 [ ] ( ) ⎧ ⎫ 3 − λ + λ − λ − λ 2 2 1 ⎨ ⎬ 1 1 cot 0 0 0 0 ⎩ ⎭ Drag Drag 4 λψ πµ 8 cU = πµ b 1 F 8 c lim = − ( ) F λ = = z ρ 2 = − λ → ∞ λ − λ − − λ 2 2 z 2 1 c a b 1 cot o − c 2 0 0 0 ( a / b ) 1 = − πµ F 6 aUK Z ME 637 ME 637 G. Ahmadi G. Ahmadi z = ξ θ ψ U ⎧ ⎫ x c sinh sin cos ρ λ 3 ⎛ ⎞ U ⎪ ⎪ − 1 λ 0 → ψ = − + λ ⎜ ⎟ 0 cot = ξ θ ψ ⎨ ⎬ y c sinh sin sin π λ + ⎝ 2 ⎠ 1 U ⎪ ⎪ = ξ θ ⎩ z c cosh cos ⎭ τ = τ 0 Let Let a a ζ = θ τ = ξ b cos cosh = − µ τ = F z 16 aU ξ = Drag Drag const const ME 637 ME 637 G. Ahmadi G. Ahmadi 5

( ) = − πµ ⎡ ⎤ τ + ⎡ τ ⎤ 2 Solution F 6 bUK Solution 1 Drag Drag − τ − 0 1 ⎢ ( ) ⎥ coth ( ) ⎢ ⎥ z τ − τ − 2 2 ⎣ ⎦ ⎣ 1 ⎦ 1 1 ψ = − ρ 0 2 U ( ) ⎡ τ + ⎤ ⎡ ⎤ τ 2 2 1 − − τ − [ ( ) ] 1 ⎧ ⎫ ( 0 ) 1 ( ) ⎥ ⎢ ⎥ coth ⎢ 3 = τ − τ + − τ − τ τ − τ − 2 2 1 0 ⎨ ⎬ 2 2 K 1 1 coth ⎣ 1 ⎦ ⎣ 1 ⎦ 0 0 0 0 0 0 ⎩ ⎭ 4 πµ 8 cU = − Drag Drag ( ) F = − 2 2 c a b − z τ + τ − τ πµ 2 1 1 coth 4 U = − 0 0 0 F a Elongated Elongated ⎛ ⎞ Z a 1 + − ⎜ ⎟ Rode Rode ln ln 2 a 1 τ = ξ = = ⎝ ⎠ cosh b 2 o o − c 2 1 ( b / a ) ME 637 ME 637 G. Ahmadi G. Ahmadi � Navier Navier- -Stokes Stokes � � Creeping Flow Creeping Flow � � Minimum Energy Minimum Energy � � Point Force Solution � Point Force Solution � � General Solution General Solution � Faxen � Faxen Law Law � Nonspherical Nonspherical Particles Particles � � Oblate Ellipsoids Oblate Ellipsoids � � Porolate Porolate Ellipsoids Ellipsoids � ME 637 ME 637 G. Ahmadi G. Ahmadi 6