Computing in carbon Basic elements of neuroelectronics -- membranes - PDF document

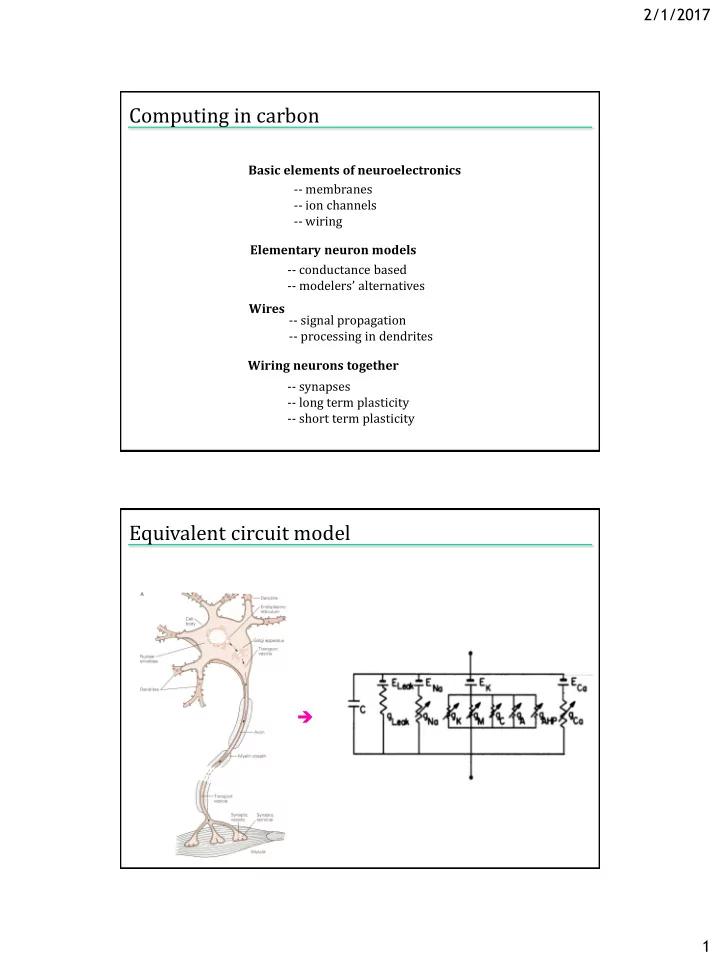
2/1/2017 Computing in carbon Basic elements of neuroelectronics -- membranes -- ion channels -- wiring Elementary neuron models -- conductance based -- modelers’ alternatives Wires -- signal propagation -- processing in dendrites Wiring neurons together -- synapses -- long term plasticity -- short term plasticity Equivalent circuit model  1

2/1/2017 Membrane patch The passive membrane Ohm’s law: Capacitor: C = Q/V Kirchhoff: 2

2/1/2017 Movement of ions through ion channels Energetics: qV ~ k B T V ~ 25mV The equilibrium potential K + Na + , Ca 2+ until opposed by Ions move down electrostatic forces their concentration gradient Nernst: 3

2/1/2017 Each ion type travels through independently Different ion channels have associated conductances . A given conductance tends to move the membrane potential toward the equilibrium potential for that ion E Na ~ 50mV depolarizing E Ca ~ 150mV depolarizing E K ~ -80mV hyperpolarizing E Cl ~ -60mV shunting E Na V > E  positive current will flow outward V V < E  positive current will flow inward 0 more polarized V rest E K Parallel paths for ions to cross membrane Several I-V curves in parallel: New equivalent circuit: 4

2/1/2017 Neurons are excitable Excitability arises from ion channel nonlinearity • Voltage dependent • transmitter dependent (synaptic) • Ca dependent 5

2/1/2017 The ion channel is a cool molecular machine K channel: open probability n describes a subunit increases when depolarized n is open probability 1 – n is closed probability Transitions between states occur at voltage dependent rates C  O P K ~ n 4 O  C Persistent conductance Transient conductances Gate acts as in previous case Additional gate can block channel when open P Na ~ m 3 h m is activation variable h is inactivation variable m and h have opposite voltage dependences: depolarization increases m , activation hyperpolarization increases h , deinactivation 6

2/1/2017 Dynamics of activation and inactivation We can rewrite: where Dynamics of activation and inactivation 7

2/1/2017 Putting it together Ohm’s law: and Kirchhoff’s law - Capacitative Ionic currents Externally current applied current The Hodgkin-Huxley equation 8

2/1/2017 Anatomy of a spike E Na E K Na ~ m 3 h K ~ m 3 h Anatomy of a spike Runaway +ve feedback E K E Na Double whammy 9

2/1/2017 Where to from here? Hodgkin-Huxley Biophysical realism Simplified models Molecular considerations Analytical tractability Geometry Ion channel stochasticity 10

2/1/2017 Microscopic models for ion channel fluctuations approach to macroscopic description Transient conductances Different from the continuous model: interdependence between inactivation and activation transitions to inactivation state 5 can occur only from 2,3 and 4 k 1 , k 2 , k 3 are constant, not voltage dependent 11

2/1/2017 The integrate-and-fire neuron Like a passive membrane: but with the additional rule that when V  V T , a spike is fired and V  V reset . E L is the resting potential of the “cell”. Exponential integrate-and-fire neuron f(V) V V reset V rest V th V max f(V) = -V + exp([V-V th ]/ D ) 12

2/1/2017 The theta neuron V spike V th V rest d q /dt = 1 – cos q + (1+ cos q ) I(t) Ermentrout and Kopell The spike response model Kernel f for subthreshold response  replaces leaky integrator Kernel for spikes  replaces “line” • determine f from the linearized HH equations • fit a threshold • paste in the spike shape and AHP Gerstner and Kistler 13

2/1/2017 Two-dimensional models w Simple™ model: V’ = -aV + bV 2 - cW W’ = -dW + eV V The generalized linear model • general definitions for k and h • robust maximum likelihood fitting procedure Truccolo and Brown, Paninski, Pillow, Simoncelli 14

2/1/2017 Dendritic computation Dendritic computation Dendrites as computational elements: Passive contributions to computation Active contributions to computation Examples 15

2/1/2017 Geometry matters Injecting current I 0 r V m = I m R m Current flows uniformly out through the cell: I m = I 0 /4 p r 2 Input resistance is defined as R N = V m (t  ∞ )/I 0 = R m /4 p r 2 Linear cables r m and r i are the membrane and axial resistances, i.e. the resistances of a thin slice of the cylinder 16

2/1/2017 Axial and membrane resistance c m r m r i For a length L of membrane cable: r i  r i L r m  r m / L c m  c m L The cable equation x x+dx (1) (2) 17

2/1/2017 The cable equation (1) (2) (1)  or Time constant where Space constant General solution: filter and impulse response Diffusive spread Exponential decay 18

2/1/2017 Voltage decays exponentially away from source Current injection at x=0, T  ∞ 0 Properties of passive cables  Electrotonic length 19

2/1/2017 Electrotonic length Johnson and Wu Properties of passive cables  Electrotonic length  Current can escape through additional pathways: speeds up decay 20

2/1/2017 Voltage rise time  Current can escape through additional pathways: speeds up decay Johnson and Wu Properties of passive cables  Electrotonic length  Current can escape through additional pathways: speeds up decay  Cable diameter affects input resistance 21

2/1/2017 Properties of passive cables  Electrotonic length  Current can escape through additional pathways: speeds up decay  Cable diameter affects input resistance  Cable diameter affects transmission velocity Step response: pulse travels Conduction velocity 22

2/1/2017 Conduction velocity www.physiol.usyd.edu/au/~daved/teaching/cv.html Other factors Finite cables Active channels 23

2/1/2017 Rall model Impedance matching: If a 3/2 = d 1 3/2 + d 2 3/2 can collapse to an equivalent cylinder with length given by electrotonic length Active cables New cable equation for each dendritic compartment 24

2/1/2017 Who’ll be my Rall model, now that my Rall model is gone Genesis, NEURON Passive computations London and Hausser, 2005 25

2/1/2017 Enthusiastically recommended references Johnson and Wu, Foundations of Cellular Physiology , Chap 4 • The classic textbook of biophysics and neurophysiology: lots of problems to work through. Good for HH, ion channels, cable theory. Koch, Biophysics of Computation • Insightful compendium of ion channel contributions to neuronal computation Izhikevich , Dynamical Systems in Neuroscience • An excellent primer on dynamical systems theory, applied to neuronal models Magee, Dendritic integration of excitatory synaptic input , • Nature Reviews Neuroscience, 2000 Review of interesting issues in dendritic integration London and Hausser, Dendritic Computation , • Annual Reviews in Neuroscience, 2005 Review of the possible computational space of dendritic processing 26