Computing GCDs for b 0 The Euclidean Proof: a = qb + r Algorithm - PowerPoint PPT Presentation

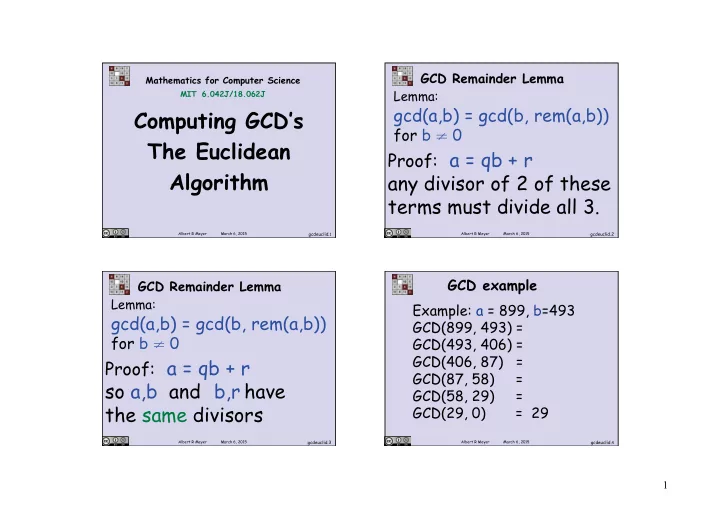
GCD Remainder Lemma Mathematics for Computer Science Lemma: MIT 6.042J/18.062J gcd(a,b) = gcd(b, rem(a,b)) Computing GCD’s for b ≠ 0 The Euclidean Proof: a = qb + r Algorithm any divisor of 2 of these terms must divide all 3. Albert R Meyer March 6, 2015 gcdeuclid. 1 Albert R Meyer March 6, 2015 gcdeuclid.2 GCD example GCD Remainder Lemma Lemma: Example: a = 899, b=493 gcd(a,b) = gcd(b, rem(a,b)) GCD(899, 493) = for b ≠ 0 GCD(493, 406) = GCD(406, 87) = Proof: a = qb + r GCD(87, 58) = so a,b and b,r have GCD(58, 29) = the same divisors GCD(29, 0) = 29 Albert R Meyer March 6, 2015 gcdeuclid.3 Albert R Meyer March 6, 2015 gcdeuclid. 4 1

GCD partial correctness Euclidean Algorithm as a State Machine: By Lemma, gcd(x,y) is constant. States ::= so preserved invariant is N × N P((x,y)) ::= [gcd(a,b) = gcd(x,y)] start ::= (a,b) state transitions defined by P(start) is trivially true: [gcd(a,b) = gcd(a,b)] (x,y) → (y, rem(x,y)) for y ≠ 0 Albert R Meyer March 6, 2015 gcdeuclid.5 Albert R Meyer March 6, 2015 gcdeuclid.6 GCD partial correctness GCD Termination at termination (if any) At each transition, x is replaced x = gcd(a,b) by y. Proof: at termination, y = 0, so x = gcd(x,0) = gcd(x,y) = gcd(a,b) preserved invariant Albert R Meyer March 6, 2015 gcdeuclid.7 Albert R Meyer March 6, 2015 gcdeuclid.8 2

GCD Termination GCD Termination At each transition, x is replaced At each transition, x is replaced by y. If y < x/2, then x gets by y. If y < x/2, then x gets halved at this step. halved at this step. If y > x/2, then rem(x,y) = x – y < x/2, so y gets halved when it is replaced by rem(x,y) after the next step. Albert R Meyer March 6, 2015 gcdeuclid.9 Albert R Meyer March 6, 2015 gcdeuclid.10 GCD Termination y halves or smaller at every other step, so reaches minimum in ≤ 2 log 2 b steps. Albert R Meyer March 6, 2015 gcdeuclid.11 3

MIT OpenCourseWare http s ://ocw.mit.edu 6.042J / 18.062J Mathematics for Computer Science Spring 20 15 For information about citing these materials or our Terms of Use, visit: http s ://ocw.mit.edu/terms.