col a
play

Col A Ax 0 1 Let W = Col A where A is m n and A = . a 1 a 2 a - PDF document

Dec 25, 2022 •223 likes •306 views

Section 6.5 Least-Squares Problem Problem: What do we do when A x = b has no solution x ? Answer: Find x such that A x is as close as possible to b . ( Least Squares Problem ) If A is m n and b is in R m , a least-squares solution

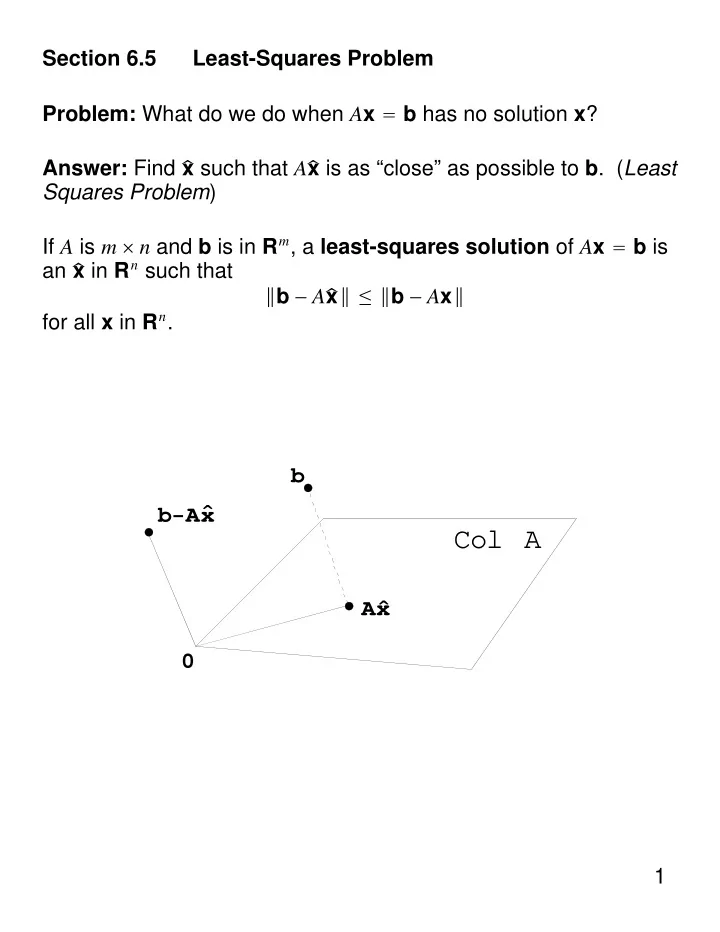
  1. Section 6.5 Least-Squares Problem Problem: What do we do when A x = b has no solution x ? Answer: Find  x such that A  x is as “close” as possible to b . ( Least Squares Problem ) If A is m × n and b is in R m , a least-squares solution of A x = b is x in R n such that an  ‖ b − A  x ‖ ≤ ‖ b − A x ‖ for all x in R n . b ˆ b − Ax Col A Ax ˆ 0 1

  2. Let W = Col A where A is m × n and A = . a 1 a 2 ⋯ a n Suppose b is in R m and b = proj W b . b z W ˆ b 0 b is the point in W = Col A closest to b 2

  3. b b − Ax ˆ Col A Ax ˆ 0 x is a vector in R n such that b = A  Since b is in Col A , then  x . 3

  4. By the Orthogonal Projection Theorem, z is in W  where z = b − A  x . Then b − A  x is orthogonal to every column of A . Meaning that T  b − A  T  b − A  T  b − A  a 1 x  = 0 a 2 x  = 0 a n x  = 0 ⋯ T a 1 0 T a 2 0  b − A  x  = ⋮ ⋮ a n T 0 A T  b − A  x  = 0 A T b − A T A  x = 0 A T A  x = A T b (normal equations for  x ) THEOREM 13 The set of least squares solutions of A x = b is the set of all solutions of the normal equations A T A  x = A T b . 4

  5. EXAMPLE: Find a least squares solution to the inconsistent system A x = b where 2 0 1 and b = . A = 0 1 2 2 2 3 Solution: Solve A T A  x = A T b after first finding A T A and A T b . 2 0 2 0 2 8 2 A T A = 0 1 = 0 1 2 4 3 2 1 1 2 0 2 8 A T b = 2 = = 0 1 2 8 3 So solve the following: 8 2 x 1 8 = 4 3 x 2 8 1 1 1 0 8 2 8 2  2 x =  ∼ 4 3 8 0 1 2 2 5

  6. When A T A is invertible, A T A  x = A T b  A T A  − 1 A T A  x =  A T A  − 1 A T b x =  A T A  − 1 A T b  So in the last example, − 1 3 − 1 8 2  A T A  − 1 = 16 8 = − 1 1 4 3 4 2 and 3 − 1 1 8 x =  A T A  − 1 A T b = 16 8  2 = − 1 1 8 2 4 2 6

  7. THEOREM 14 The matrix A T A is invertible if and only if the columns of A are linearly independent. In this case, the equation A x = b has only one least-squares solution  x , and it is given by x =  A T A  − 1 A T b .  least-squares error = ‖ b − A  x ‖ From the last example, 1 2 0 1 1 and A  2 b = x = 2 0 1 2 = 2 3 2 2 5 1 1 least-squares error = ‖ b − A  x ‖ = = 2 2 2 − 3 5 7

  8. b b − Ax ˆ Col A Ax ˆ 0 For another way to compute  x , see Theorem 15 (page 414) and Example 5, page 415. 8

Recommend

More recommend