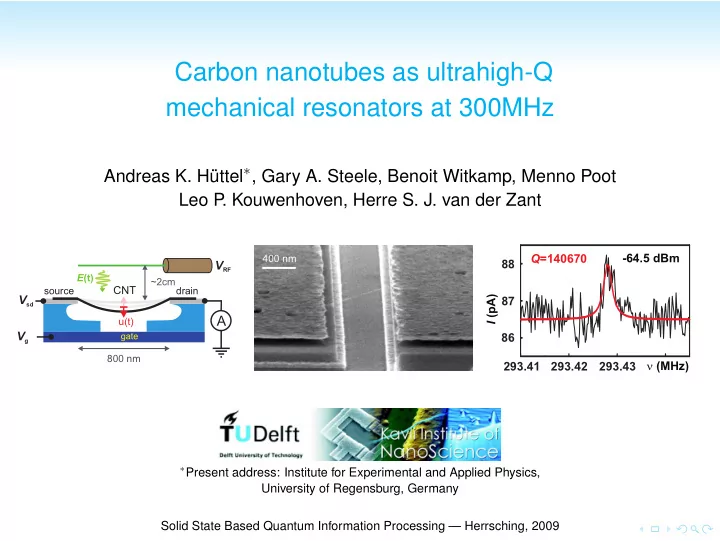
Carbon nanotubes as ultrahigh-Q mechanical resonators at 300MHz - PowerPoint PPT Presentation

Carbon nanotubes as ultrahigh-Q mechanical resonators at 300MHz uttel ∗ , Gary A. Steele, Benoit Witkamp, Menno Poot Andreas K. H¨ Leo P . Kouwenhoven, Herre S. J. van der Zant -64.5 dBm 400 nm Q =140670 88 V RF E (t) ~2cm source CNT drain V sd I (pA) 87 A u(t) V g gate 86 800 nm 293.41 293.42 293.43 � (MHz) ∗ Present address: Institute for Experimental and Applied Physics, University of Regensburg, Germany Solid State Based Quantum Information Processing — Herrsching, 2009

Nanotubes as beam resonators — up to now complicated setup — even at 1K, maximally Q ≃ 2000 Ultrasensitive Mass Sensing with a Nanotube Electromech. Atomic-Scale Mass Sensing Using Carbon Resonator Nanotube Resonators B. Lassagne, D. Garcia-Sanchez, A. Aguasca and A. Hsin-Ying Chiu, Peter Hung, Henk W. Ch. Bachtold Postma and Marc Bockrath Nano Lett., 2008, 8 (11), pp 3735–373 Nano Lett., 2008, 8 (12), pp 4342–434

Why low Q? Many possible reasons. • HF cables directly to sample: heating, noise • Contamination of the nanotubes during lithography • Clamping points?

Chip fabrication and measurement setup 400 nm V RF E (t) ~2cm source drain CNT V sd A V g gate 800 nm • Basic chip geometry and fabrication as already shown by Georg G¨ otz • Additional wet-etch step to suspend the nanotube over full length • All gate areas connected to a single gate voltage source V g • RF antenna suspended ∼ 2cm above chip • Dilution refrigerator ( T ≃ 20mK) • Only dc measurement A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

dc Coulomb blockade measurement — beautiful diamonds I (nA) |I| (pA) 2 V sd (mV) 1 10000 0 1000 0.5 100 10 -2 0 1 -4.4 -4.2 V g (V) -4.0 -0.88 -0.86 -0.84 -0.82 V g (V) highly regular quantum dot within the nanotube source dot drain � V g � S N el. � S � D � S � D � D V SD I � Dot V g gate CB SET A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Fixed V g and V SD , sweep of RF signal frequency 2 Q =140670 -17.8 dBm -64.5 dBm 88 I (pA) I (nA) 87 1 86 0 100 300 500 293.41 293.42 293.43 293.44 � (MHz) � (MHz) • Sharp resonant structure in I dc ( ν ) • Very low driving power required • From FWHM, Q ≃ 140000 A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

V g dependence — this is really a mechanical resonance! � (MHz) 350 red: continuum beam model 300 � (MHz) 250 300 200 150 d I 250 d � -6 -5 -4 -3 -2 -1 0 V g (V) (pA/MHz) 1000 200 100 150 10 -6 -4 -2 V g (V) 0 A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Detection mechanism — mechanically induced averaging 0.6 1.5 V g =−5.17V V g =−5.16V 2 I (nA) I (nA) � I ac,eff V g 1 0 0 0 285 305 285 305 -5.22 -5.21 -5.2 -5.19 � (MHz) � (Mhz) V g (V) • at resonant driving the nanotube position oscillates • oscillating C g − → averaging over CB oscillations amplitude calculated from I ( V ) DC g 0.1 � I (nA) 0 -0.1 ac,eff =1mV V g measured resonance amplitude I max ( ) � � -5.22 -5.21 -5.2 -5.19 -5.22 -5.21 -5.2 -5.19 V g (V) V g (V) A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Some numbers • Resonance frequency 120MHz � ν � 360MHz • Zero-tension frequency consistent with CNT diameter from band gap • V g dependence of frequency consistent with bending vibration mode • Quality factor up to Q ≃ 150000 • Estimated motion amplitude at resonant driving ∼ 250pm compare thermal motion 6 . 5pm, zero-point motion 1 . 9pm A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Driving into nonlinear response... 80 mK, -70 dBm I (pA) • same temperature • same working point V g , V SD -62 dBm I (pA) I (pA) • low driving power: symmetric, “linear” response -56 dBm I (pA) • high driving power: asymmetric response, hysteresis -52.5 dBm Duffing-like oscillator I (pA) � (MHz) A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

... and then increasing the temperature -53 dBm, 20mK I (pA) • same driving power • same working point V g , V SD 80mK I (pA) • low temperature: asymmetric response, hysteresis 120mK Duffing-like oscillator I (pA) • high temperature: symmetric, “linear” response 160mK I (pA) peak broadening � (MHz) A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Temperature dependence of Q (a) -66 dBm, 40mK I (pA) 5 Q=123578 10 -0.36 ~ T Q-factor (b) -50.5 dBm, 320mK I (pA) Q=59283 (c) -45 dBm, 1K I (pA) Q=23210 4 10 0.01 0.1 1 � (MHz) Temperature (K) Q ( T ) fits power law prediction for intrinsic dissipation in nanotube → H. Jiang et al. , Phys. Rev. Lett. 93 , 185501 (2004) − A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h

Summary & outlook, but no conclusion yet! • Nanotube as light, extremely tunable high- Q RF resonator • Self-detection of motion via dc current • Easy driving into nonlinear oscillator regime • Q ( T ) is consistent with intrinsic dissipation model u • Application as mass sensor: sensitivity 4 . 2 √ Hz • Without driving: mechanical thermal occupation n ≃ 1 . 2 • “Large-scale phenomena” of the system – but stay tuned for more! A. K. H¨ uttel et al. , NanoLett. ASAP (2009), doi:10.1021/nl900612h