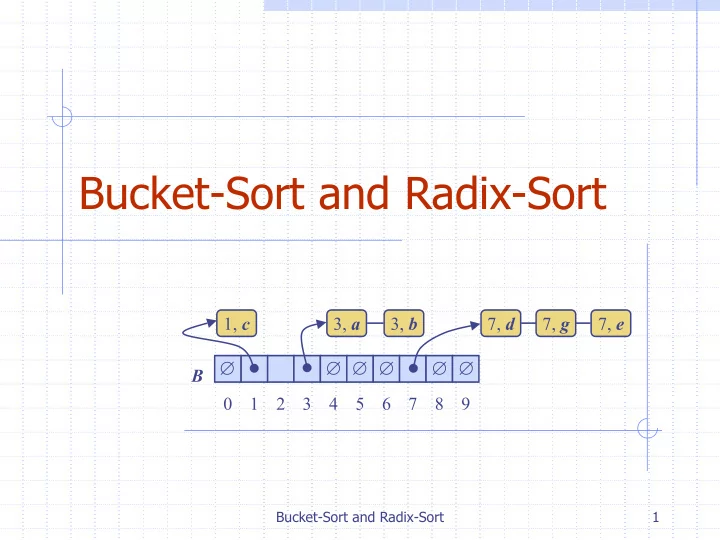
Bucket-Sort and Radix-Sort 1, c 3, a 3, b 7, d 7, g 7, e - PowerPoint PPT Presentation

Bucket-Sort and Radix-Sort 1, c 3, a 3, b 7, d 7, g 7, e ∅ ∅ ∅ ∅ ∅ ∅ ∅ B 0 1 2 3 4 5 6 7 8 9 Bucket-Sort and Radix-Sort 1

Bucket-Sort (§10.5.1) Let be S be a sequence of n Algorithm bucketSort ( S, N ) (key, element) items with keys Input sequence S of (key, element) in the range [0, N − 1] items with keys in the range [0, N − 1] Bucket-sort uses the keys as Output sequence S sorted by indices into an auxiliary array B increasing keys of sequences (buckets) B ← array of N empty sequences Phase 1: Empty sequence S by while ¬ S.isEmpty () moving each item ( k , o ) into its bucket B [ k ] f ← S.first () Phase 2: For i = 0, … , N − 1 , move ( k , o ) ← S.remove ( f ) the items of bucket B [ i ] to the B [ k ] .insertLast (( k , o )) end of sequence S for i ← 0 to N − 1 Analysis: while ¬ B [ i ] .isEmpty () � Phase 1 takes O ( n ) time f ← B [ i ] .first () � Phase 2 takes O ( n + N ) time ( k , o ) ← B [ i ] .remove ( f ) Bucket-sort takes O ( n + N ) time S.insertLast (( k , o )) Bucket-Sort and Radix-Sort 2

Example Key range [0, 9] 7, d 1, c 3, a 7, g 3, b 7, e Phase 1 1, c 3, a 3, b 7, d 7, g 7, e B ∅ ∅ ∅ ∅ ∅ ∅ ∅ 0 1 2 3 4 5 6 7 8 9 Phase 2 1, c 3, a 3, b 7, d 7, g 7, e Bucket-Sort and Radix-Sort 3

Properties and Extensions Extensions Key-type Property � Integer keys in the range [ a , b ] � The keys are used as � Put item ( k , o ) into bucket indices into an array B [ k − a ] and cannot be arbitrary � String keys from a set D of objects possible strings, where D has � No external comparator constant size (e.g., names of the 50 U.S. states) Stable Sort Property � Sort D and compute the rank � The relative order of r ( k ) of each string k of D in any two items with the the sorted sequence same key is preserved � Put item ( k , o ) into bucket after the execution of B [ r ( k )] the algorithm Bucket-Sort and Radix-Sort 4

Lexicographic Order A d- tuple is a sequence of d keys ( k 1 , k 2 , … , k d ) , where key k i is said to be the i- th dimension of the tuple Example: � The Cartesian coordinates of a point in space are a 3-tuple The lexicographic order of two d- tuples is recursively defined as follows ( x 1 , x 2 , … , x d ) < ( y 1 , y 2 , … , y d ) ⇔ x 1 < y 1 ∨ x 1 = y 1 ∧ ( x 2 , … , x d ) < ( y 2 , … , y d ) I.e., the tuples are compared by the first dimension, then by the second dimension, etc. Bucket-Sort and Radix-Sort 5

Lexicographic-Sort Algorithm lexicographicSort ( S ) Let C i be the comparator that compares two tuples by Input sequence S of d -tuples their i- th dimension Output sequence S sorted in lexicographic order Let stableSort ( S , C ) be a stable sorting algorithm that uses comparator C for i ← d downto 1 Lexicographic-sort sorts a stableSort ( S , C i ) sequence of d- tuples in lexicographic order by Example: executing d times algorithm stableSort , one per (7,4,6) (5,1,5) (2,4,6) (2, 1, 4) (3, 2, 4) dimension (2, 1, 4) (3, 2, 4) (5,1,5) (7,4,6) (2,4,6) Lexicographic-sort runs in O ( dT ( n )) time, where T ( n ) is (2, 1, 4) (5,1,5) (3, 2, 4) (7,4,6) (2,4,6) the running time of (2, 1, 4) (2,4,6) (3, 2, 4) (5,1,5) (7,4,6) stableSort Bucket-Sort and Radix-Sort 6

Radix-Sort (§10.5.2) Radix-sort is a specialization of lexicographic-sort that uses bucket-sort as the stable sorting algorithm in each dimension Algorithm radixSort ( S, N ) Input sequence S of d -tuples such Radix-sort is applicable that (0 , …, 0) ≤ ( x 1 , …, x d ) and to tuples where the ( x 1 , …, x d ) ≤ ( N − 1 , …, N − 1) keys in each dimension i for each tuple ( x 1 , …, x d ) in S are integers in the Output sequence S sorted in range [0 , N − 1] lexicographic order Radix-sort runs in time for i ← d downto 1 O ( d ( n + N )) bucketSort ( S , N ) Bucket-Sort and Radix-Sort 7

Radix-Sort for Binary Numbers Consider a sequence of n b -bit integers x = x b − 1 … x 1 x 0 Algorithm binaryRadixSort ( S ) We represent each element Input sequence S of b -bit as a b -tuple of integers in integers the range [0, 1] and apply Output sequence S sorted radix-sort with N = 2 replace each element x This application of the of S with the item (0 , x ) radix-sort algorithm runs in for i ← 0 to b − 1 O ( bn ) time replace the key k of each item ( k, x ) of S For example, we can sort a with bit x i of x sequence of 32-bit integers bucketSort ( S, 2) in linear time Bucket-Sort and Radix-Sort 8

Example Sorting a sequence of 4-bit integers 1001 0010 1001 1001 0001 0010 1110 1101 0001 0010 1101 1001 0001 0010 1001 0001 1101 0010 1101 1101 1110 0001 1110 1110 1110 Bucket-Sort and Radix-Sort 9