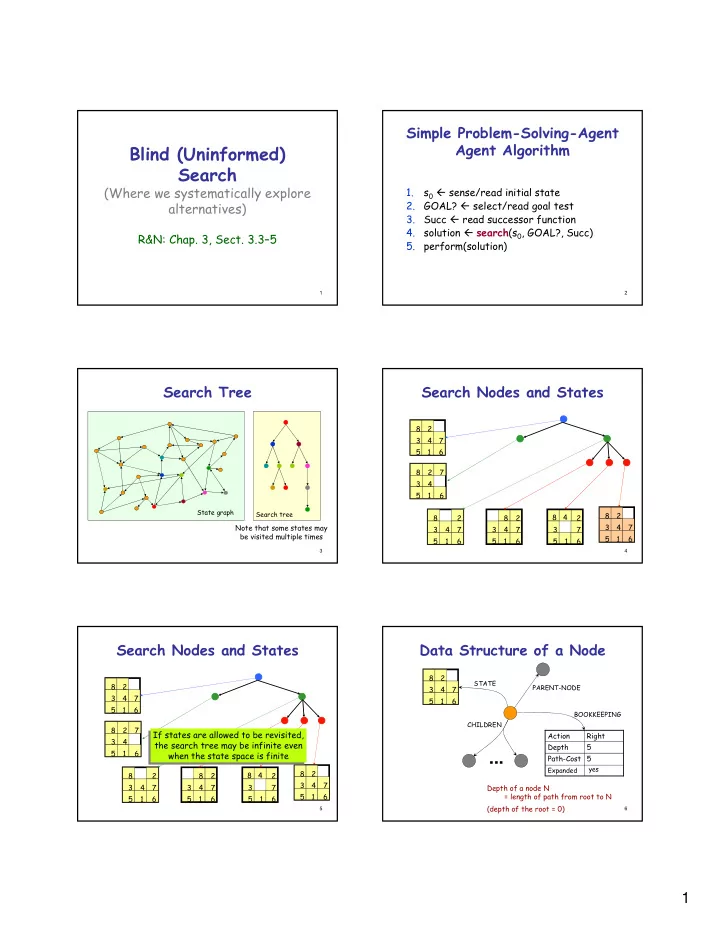

Simple Problem-Solving-Agent Agent Algorithm Blind (Uninformed) Search (Where we systematically explore 1. s 0 � sense/read initial state 2. GOAL? � select/read goal test alternatives) 3. Succ � read successor function 4. solution � search (s 0 , GOAL?, Succ) R&N: Chap. 3, Sect. 3.3–5 5. perform(solution) 1 2 Search Tree Search Nodes and States 8 2 3 4 7 5 1 6 8 2 7 3 4 5 1 6 State graph Search tree 8 2 8 2 8 2 8 4 2 3 4 7 Note that some states may 3 4 7 3 4 7 3 7 be visited multiple times 5 1 6 5 1 6 5 1 6 5 1 6 3 4 Search Nodes and States Data Structure of a Node 8 2 STATE 8 2 PARENT-NODE 3 4 7 3 4 7 5 1 6 5 1 6 BOOKKEEPING CHILDREN 8 2 7 If states are allowed to be revisited, Action Right If states are allowed to be revisited, 3 4 the search tree may be infinite even the search tree may be infinite even Depth 5 5 1 6 when the state space is finite when the state space is finite Path-Cost 5 ... yes Expanded 8 2 8 2 8 2 8 4 2 3 4 7 3 4 7 3 4 7 3 7 Depth of a node N 5 1 6 = length of path from root to N 5 1 6 5 1 6 5 1 6 (depth of the root = 0) 5 6 1
Node expansion Fringe of Search Tree 8 2 The expansion of a node N of the 3 4 7 search tree consists of: � The fringe is the set of all search nodes 5 1 6 1) Evaluating the successor that haven’t been expanded yet N function on STATE (N) 2) Generating a child of N for 8 2 each state returned by the 3 4 7 function 5 1 6 node generation ≠ node expansion 8 2 7 3 4 5 1 6 8 2 8 4 8 2 2 3 4 7 8 2 3 4 7 3 7 8 4 8 2 8 2 2 3 4 7 5 1 6 3 4 7 3 4 7 3 7 5 1 6 5 1 6 5 1 6 5 1 6 5 1 6 5 1 6 7 8 Search Strategy � The fringe is the set of all search nodes that haven’t been expanded yet � The fringe is implemented as a priority queue FRINGE • INSERT(node,FRINGE) • REMOVE(FRINGE) Is it identical � The ordering of the nodes in FRINGE to the set of leaves? defines the search strategy 9 10 Search Algorithm #1 Performance Measures SEARCH#1 � Completeness 1. If GOAL?(initial-state) then return initial-state A search algorithm is complete if it finds a 2. INSERT(initial-node,FRINGE) solution whenever one exists 3. Repeat: [What about the case when no solution exists?] a. If empty(FRINGE) then return failure � Optimality b. N � REMOVE(FRINGE) Expansion of N A search algorithm is optimal if it returns a c. s � STATE(N) minimum-cost path whenever a solution exists d. For every state s’ in SUCCESSORS(s) � Complexity i. Create a new node N’ as a child of N ii. If GOAL?(s’) then return path or goal state It measures the time and amount of memory iii. INSERT(N’,FRINGE) required by the algorithm 11 12 2
Blind vs. Heuristic Strategies Example For a blind strategy, N 1 and N 2 � Blind (or un-informed) strategies do not are just two nodes (at some 8 2 position in the search tree) exploit state descriptions to order STATE 3 4 7 FRINGE. They only exploit the positions N 1 5 1 6 of the nodes in the search tree 1 2 3 � Heuristic (or informed) strategies 1 2 3 4 5 6 exploit state descriptions to order STATE 4 5 7 8 FRINGE (the most “promising” nodes N 2 Goal state 7 8 6 are placed at the beginning of FRINGE) 13 14 Example Remark For a heuristic strategy counting � Some search problems, such as the (n 2 -1)- the number of misplaced tiles, 8 2 puzzle, are NP-hard N 2 is more promising than N 1 STATE � One can’t expect to solve all instances of 3 4 7 N 1 such problems in less than exponential 5 1 6 time (in n) 1 2 3 � One may still strive to solve each instance 1 2 3 4 5 6 as efficiently as possible STATE 4 5 7 8 � This is the purpose of the search strategy N 2 Goal state 7 8 6 15 16 Blind Strategies Breadth-First Strategy � Breadth-first New nodes are inserted at the end of FRINGE • Bidirectional 1 Arc cost = 1 � Depth-first • Depth-limited FRINGE = (1) 2 3 • Iterative deepening 4 5 6 7 Arc cost � Uniform-Cost = c(action) ≥ ε > 0 (variant of breadth-first) 17 18 3
Breadth-First Strategy Breadth-First Strategy New nodes are inserted at the end of FRINGE New nodes are inserted at the end of FRINGE 1 1 FRINGE = (2, 3) FRINGE = (3, 4, 5) 2 3 2 3 4 5 6 7 4 5 6 7 19 20 Breadth-First Strategy Important Parameters 1) Maximum number of successors of any state New nodes are inserted at the end of FRINGE � branching factor b of the search tree 1 2) Minimal length ( ≠ cost) of a path between FRINGE = (4, 5, 6, 7) 2 3 the initial and a goal state 4 5 6 7 � depth d of the shallowest goal node in the search tree 21 22 Evaluation Evaluation � b: branching factor � b: branching factor � d: depth of shallowest goal node � d: depth of shallowest goal node � Breadth-first search is: � Breadth-first search is: • Complete? Not complete? • Complete • Optimal? Not optimal? • Optimal if step cost is 1 � Number of nodes generated: ??? 23 24 4
Evaluation Evaluation � b: branching factor � b: branching factor � d: depth of shallowest goal node � d: depth of shallowest goal node � Breadth-first search is: � Breadth-first search is: • Complete • Complete • Optimal if step cost is 1 • Optimal if step cost is 1 � Number of nodes generated: � Number of nodes generated: 1 + b + b 2 + … + b d = ??? 1 + b + b 2 + … + b d = (b d+1 -1)/(b-1) = O(b d ) � � Time and space complexity is O(b d ) 25 26 Big O Notation Time and Memory Requirements d # Nodes Time Memory g(n) = O(f(n)) if there exist two positive 2 111 .01 msec 11 Kbytes constants a and N such that: 4 11,111 1 msec 1 Mbyte for all n > N: g(n) ≤ a × f(n) 6 ~10 6 1 sec 100 Mb 8 ~10 8 100 sec 10 Gbytes 10 ~10 10 2.8 hours 1 Tbyte 12 ~10 12 11.6 days 100 Tbytes 14 ~10 14 3.2 years 10,000 Tbytes Assumptions: b = 10; 1,000,000 nodes/sec; 100bytes/node 27 28 Remark Time and Memory Requirements If a problem has no solution, breadth-first may d # Nodes Time Memory run for ever (if the state space is infinite or states can be revisited arbitrary many times) 2 111 .01 msec 11 Kbytes 4 11,111 1 msec 1 Mbyte 1 2 3 4 1 2 3 4 6 ~10 6 1 sec 100 Mb 8 ~10 8 100 sec 10 Gbytes 5 6 7 8 ? 5 6 7 8 10 ~10 10 2.8 hours 1 Tbyte 12 ~10 12 11.6 days 100 Tbytes 9 10 11 12 9 10 11 12 14 ~10 14 3.2 years 10,000 Tbytes 13 14 15 13 15 14 Assumptions: b = 10; 1,000,000 nodes/sec; 100bytes/node 29 30 5
Bidirectional Strategy Depth-First Strategy 2 fringe queues: FRINGE1 and FRINGE2 New nodes are inserted at the front of FRINGE s 1 2 3 FRINGE = (1) 4 5 Time and space complexity is O(b d/2 ) << O(b d ) if both trees have the same branching factor b Question: What happens if the branching factor is different in each direction? 31 32 Depth-First Strategy Depth-First Strategy New nodes are inserted at the front of FRINGE New nodes are inserted at the front of FRINGE 1 1 2 3 2 3 FRINGE = (2, 3) FRINGE = (4, 5, 3) 4 5 4 5 33 34 Depth-First Strategy Depth-First Strategy New nodes are inserted at the front of FRINGE New nodes are inserted at the front of FRINGE 1 1 2 3 2 3 4 5 4 5 35 36 6
Depth-First Strategy Depth-First Strategy New nodes are inserted at the front of FRINGE New nodes are inserted at the front of FRINGE 1 1 2 3 2 3 4 5 4 5 37 38 Depth-First Strategy Depth-First Strategy New nodes are inserted at the front of FRINGE New nodes are inserted at the front of FRINGE 1 1 2 3 2 3 4 5 4 5 39 40 Depth-First Strategy Depth-First Strategy New nodes are inserted at the front of FRINGE New nodes are inserted at the front of FRINGE 1 1 2 3 2 3 4 5 4 5 41 42 7
Evaluation Evaluation � b: branching factor � b: branching factor � d: depth of shallowest goal node � d: depth of shallowest goal node � m: maximal depth of a leaf node � m: maximal depth of a leaf node � Depth-first search is: � Depth-first search is: � Complete? � Complete only for finite search tree � Optimal? � Not optimal � Number of nodes generated (worst case): 1 + b + b 2 + … + b m = O(b m ) � Time complexity is O(b m ) � Space complexity is O(bm) [or O(m)] [Reminder: Breadth-first requires O(b d ) time and space] 43 44 Depth-Limited Search Iterative Deepening Search Provides the best of both breadth-first � Depth-first with depth cutoff k (depth and depth-first search at which nodes are not expanded) Totally horrifying ! Main idea: � Three possible outcomes: IDS • Solution For k = 0, 1, 2, … do: • Failure (no solution) Perform depth-first search with • Cutoff (no solution within cutoff) depth cutoff k (i.e., only generate nodes with depth ≤ k) 45 46 Iterative Deepening Iterative Deepening 47 48 8
Recommend
More recommend