Binary Search Trees Data Structures and Algorithms CSE 373 SP 18 - - PowerPoint PPT Presentation

Binary Search Trees Data Structures and Algorithms CSE 373 SP 18 - KASEY CHAMPION 1

Warm Up From CS CSE 143 43: - what is a “binary tree” - how do you write code to build a tree from scratch? - how do you write code to traverse an existing tree? - how do you write code to change an existing tree? - What is the runtime to traverse a tree and print out every node? Socrative: www.socrative.com Room Name: CSE373 Please enter your name as: Last, First CSE 373 SP 18 - KASEY CHAMPION 2

Storing Sorted Items in an Array get() – O(logn) put() – O(n) remove() – O(n) Can we do better with insertions and removals? CSE 373 SP 18 - KASEY CHAMPION 3

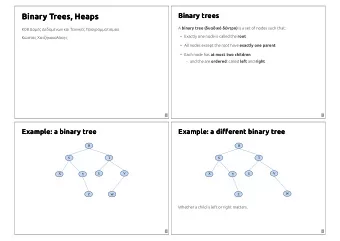
Trees! A tree is a collection of nodes 1 - Each node has at most 1 parent and 0 or more children Root node: e: the single node with no parent, “top” of 2 5 the tree Branc nch h node: e: a node with one or more children Leaf f node: e: a node with no children 3 7 6 Edge: : a pointer from one node to another Subtree: ee: a node and all it descendants 4 8 Heig ight: ht: the number of edges contained in the longest path from root node to some leaf node CSE 373 SP 18 - KASEY CHAMPION 4

Tree Height What is the height of the following trees? overallRoot overallRoot overallRoot null 1 7 2 5 7 Height = 2 Height = 0 Height = -1 or NA CSE 373 SP 18 - KASEY CHAMPION 5

Traversals trave aversal al: An examination of the elements of a tree. – A pattern used in many tree algorithms and methods Common orderings for traversals: overallRoot – pre-order er: process root node, then its left/right subtrees – 17 41 29 6 9 81 40 – in in-or order er: process left subtree, then root node, then right 17 – 29 41 6 17 81 9 40 – post-or order er: process left/right subtrees, then root node – 29 6 41 81 40 9 17 41 9 Traversal Trick: Sailboat method – Trace a path around the tree. – As you pass a node on the 29 6 81 40 proper side, process it. • pre-order: left side • in-order: bottom • post-order: right side CSE 373 SP 17 – ZORA FUNG 6

Binary Search Trees A bina nary y search ch tree e is a binary tree that contains comparable items such that for every node, all children to the left contain smaller data and all children to the right contain larger data. 10 9 15 7 18 12 8 17 CSE 373 SP 18 - KASEY CHAMPION 7

Implement Dictionary 10 “foo” Binary Search Trees allow us to: - quickly find what we’re looking for 12 7 - add and remove values easily “ baz ” “bar” Dictionary Operations: Runtime in terms of height, “h” get() – O(h) 15 5 9 put() – O(h) “sup” “ fo ” “ sho ” remove() – O(h) What do you replace the node with? Largest in left sub tree or smallest in right sub tree 1 8 13 “burp” “poo” “boo” CSE 373 SP 18 - KASEY CHAMPION 8

CSE 373 SP 18 - KASEY CHAMPION 9