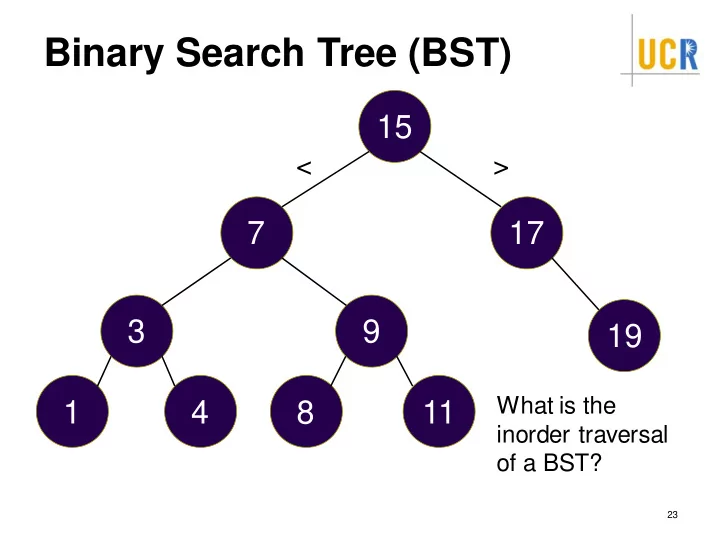
Binary Search Tree (BST) 15 < > 7 17 3 9 19 What is - PowerPoint PPT Presentation

Aug 23, 2022 •200 likes •369 views

Binary Search Tree (BST) 15 < > 7 17 3 9 19 What is the 1 4 8 11 inorder traversal of a BST? 23 BST Definition BST is a binary tree Each node stores a value from an ordered domain, e.g., numbers or strings The value of any

Binary Search Tree (BST) 15 < > 7 17 3 9 19 What is the 1 4 8 11 inorder traversal of a BST? 23
BST Definition BST is a binary tree Each node stores a value from an ordered domain, e.g., numbers or strings The value of any node is ≥ all values in the left subtree, and ≤ all values in the right subtree 24
BST ADT Initialize() – Initializes an empty BST Find(x) – Searches for x in the tree and returns true or false Insert(x) – Inserts the value x into the BST Delete(x) – Deletes the value x from the tree if it is in the tree FindMin() – Returns the minimum value in the tree without deleting it FindMax() – Returns the maximum value in the tree without deleting it 25
BST.Find Find 8 15 Find 14 7 17 3 9 19 1 4 8 11 26
BST.Find bool find(Node* node, T x) { if (node == null) return false ; if (x == node.value) return true ; if (x < node.value) find(node.____, x); if (x > node.value) find(node.____, x); } 27
BST.Find bool find(Node* node, T x) { if (node == null) return false ; if (x == node.value) return true ; if (x < node.value) find(node.left, x); if (x > node.value) find(node.right, x); FindMin() } FindMax() 28
BST.Insert Insert 18 15 7 17 3 9 19 1 4 8 11 18 29
BST.Insert Insert 14 15 7 17 3 9 19 1 4 8 11 18 14 30
BST.Remove Remove 11 15 7 17 3 9 19 1 4 8 11 31
BST.Remove Remove 9 15 7 17 3 9 19 1 4 8 32
BST.Remove Remove 7 15 7 17 3 9 19 1 4 8 11 33
BST.Remove Remove 7 15 17 3 9 19 1 4 8 11 34
BST.Remove Remove 7 15 17 3 9 19 1 4 8 11 35
BST.Remove Remove 7 15 8 17 3 9 19 1 4 11 36
BST.Remove Remove 7 15 8 17 3 9 19 1 4 11 37
Analysis of BST Algorithms Operations: Find Insert FindMin FindMax Delete All O(h) where h is the height of the tree h = O(n) (worst case) h = Ω (log n) (best case) How to guarantee O(log n) performance? 38

Recommend

Definitions Binary Search Tree: n Tree: hierarchical structure made of nodes with father-son

Advanced Programming Binary Search Tree Binary Search Tree Introduction Binary Search Tree, o BST implement dictionaries or ordered queues elements stored are ordered according to a key Efficient (log n) operations S EARCH , M INIMUM , M

362 views • 32 slides

Binary Search Trees A binary search tree is a binary tree T such that - each internal node

AVL T REES Binary Search Trees AVL Trees AVL Trees 1 Binary Search Trees A binary search tree is a binary tree T such that - each internal node stores an item (k, e) of a dictionary. - keys stored at nodes in the left subtree of

547 views • 26 slides

Balanced Search Trees Binary Search Trees Binary Search Tree Binary Search Tree A binary tree is

Balanced Search Trees Binary Search Trees Binary Search Tree Binary Search Tree A binary tree is a binary search tree if each element in the left subtree is smaller than the root, each element in the right subtree is larger than the root,

757 views • 51 slides

Binary search trees Dictionary ADT Binary search tree properties Search Insertion February 04,

Binary search trees Dictionary ADT Binary search tree properties Search Insertion February 04, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 1 By the way... Here is a reference to the "three dots" tree traversal shown in

602 views • 17 slides

CMSC 206 Binary Search Trees 1 Binary Search Tree n A Binary Search Tree is a Binary Tree in

CMSC 206 Binary Search Trees 1 Binary Search Tree n A Binary Search Tree is a Binary Tree in which, at every node v, the values stored in the left subtree of v are less than the value at v and the values stored in the right subtree are

280 views • 25 slides

Binary Search Trees and Balanced Binary Search Trees using AVL Trees Mark Redekopp David Kempe

1 CSCI 104 Binary Search Trees and Balanced Binary Search Trees using AVL Trees Mark Redekopp David Kempe Sandra Batista 2 Properties, Insertion and Removal BINARY SEARCH TREES 3 Binary Search Tree Binary search tree = binary tree

630 views • 61 slides

binary search trees Oct. 30, 2017 1 (binary search) tree binary (search tree) 2 class

COMP 250 Lecture 22 binary search trees Oct. 30, 2017 1 (binary search) tree binary (search tree) 2 class BSTNode< K >{ K key; BSTNode< K > leftchild; BSTNode< K > rightchild; : } The

745 views • 48 slides

Binary Search Trees Understand tree terminology Understand and implement tree

Binary Search Trees Understand tree terminology Understand and implement tree traversals Define the binary search tree property Implement binary search trees Implement the TreeSort algorithm October 2004 John Edgar 2

707 views • 66 slides

This is a slide Group Philsophy Binary Search Tree (BST) A binary search tree 12 5 15 3

This is a slide Group Philsophy Binary Search Tree (BST) A binary search tree 12 5 15 3 8 16 17 4 6 9 7 Binary Search Tree 2 Construct binary search tree Input[2, 4, 5, 1, 3] 1 4 3 5 O(logN) What if the input

470 views • 25 slides

Week 8 Oliver Kullmann Binary trees The notion BinaryTrees of binary search tree Tree

CS 270 Algorithms Week 8 Oliver Kullmann Binary trees The notion BinaryTrees of binary search tree Tree traversal Binary trees 1 Queries in binary The notion of binary search tree search trees 2 Insertion Tree

1.02k views • 49 slides

overview tree traversals data structures and algorithms binary search 2020 10 01 lecture 10

overview tree traversals data structures and algorithms binary search 2020 10 01 lecture 10 binary search trees overview recap definitions binary tree: every node has at most 2 successors (empty tree is also a binary tree) tree traversals

399 views • 10 slides

Objectives To design and implement a binary search tree (25.2). To represent binary trees

Chapter 25 Binary Search Trees Liang, Introduction to Java Programming, Tenth Edition, (c) 2013 Pearson Education, Inc. All 1 rights reserved. Objectives To design and implement a binary search tree (25.2). To represent binary trees

443 views • 18 slides

CS 310 Advanced Data Structures and Algorithms Binary Search Tree June 26, 2017 Tong Wang

CS 310 Advanced Data Structures and Algorithms Binary Search Tree June 26, 2017 Tong Wang UMass Boston CS 310 June 26, 2017 1 / 30 Binary Search Tree A binary search tree is a binary tree: If y is a node in the left subtree of x, then

343 views • 30 slides

Chapter 6 AVL Search Trees The efficiency of binary search tree depends on the shape of the

CS 2412 Data Structures Chapter 6 AVL Search Trees The efficiency of binary search tree depends on the shape of the tree. If an ordered or almost ordered sequence of data are inserted to a binary tree, then the search is not efficient. ( O (

772 views • 64 slides

How efficient are binary search trees? Balanced search trees Balancing a tree means to keep the

CS206 CS206 How efficient are binary search trees? Balanced search trees Balancing a tree means to keep the left and right subtree of Binary search tree operations take time O ( h ) , where h is the every node of roughly equal size.

200 views • 3 slides

Binary search trees Traversals (continued) Dictionary ADT Binary search tree February 12, 2020

Binary search trees Traversals (continued) Dictionary ADT Binary search tree February 12, 2020 Cinda Heeren / Andy Roth / Geoffrey Tien 1 Announcements Final exam: Monday, Apr.20, 15:30 18:00 Location(s) TBA February 12, 2020

522 views • 21 slides

Trees Tiziana Ligorio 1 Todays Plan Trees Binary Tree ADT Binary Search Tree ADT 2

Trees Tiziana Ligorio 1 Todays Plan Trees Binary Tree ADT Binary Search Tree ADT 2 Announcements Questions? 3 ADT Operations we have seen so far Bag, List, Stack, Queue Add data to collection Remove data from

1.44k views • 117 slides

Search Algorithms II 15-110 Wednesday 10/21 Learning Objectives Identify whether or not a

Search Algorithms II 15-110 Wednesday 10/21 Learning Objectives Identify whether or not a tree is a binary search tree Search for values in binary search trees using binary search Understand how and why hashing makes it possible to

762 views • 43 slides

7 4 12 2 6 9 19 3 5 8 11 15 20 2 Traversal of the Nodes in a BST By traversal

Chapter 12: Binary Search Trees A binary search tree is a binary tree with a special property called the BST-property , which is given as follows: For all nodes x and y , if y belongs to the left subtree of x , then the key at y is less than

641 views • 26 slides

Trees Linear Vs non-linear data structures Types of binary trees Binary tree traversals

Trees Linear Vs non-linear data structures Types of binary trees Binary tree traversals Representations of a binary tree Binary tree ADT Binary search tree EECS 268 Programming II 1 Overview We have discussed linear

1.05k views • 76 slides

Red-Black Trees ! Motivation: a binary search tree that is guaranteed to be balanced (operations

Red-Black Trees ! Motivation: a binary search tree that is guaranteed to be balanced (operations take time in the ( ) O lg n worst-case). Red-Black Trees ! A red-black tree is a binary search tree where each node has a color

259 views • 4 slides

Binary Search Tree intro BST with order properties After today, you should be able to

Binary Search Tree intro BST with order properties After today, you should be able to implement deletion from a BST Partner Evaluation done? Q/A and Work time today, 2 nd hour Binary Trees that store elements in increasing order

91 views • 8 slides

Costliness of contains Review: in a binary tree, contains is O(N) contains may be a

Costliness of contains Review: in a binary tree, contains is O(N) contains may be a frequent operation in an application CSE 143 Can we do better than O(N)? Turn to list searching for inspiration... Why was binary search so much

152 views • 4 slides

10/17/2016 Review: Binary Search Trees (BST) Structure property (binary tree) Each node

10/17/2016 Review: Binary Search Trees (BST) Structure property (binary tree) Each node has 2 children 8 Result: keeps operations simple CSE373: Data Structures and Algorithms Order property 5 11 AVL Trees All keys

202 views • 7 slides