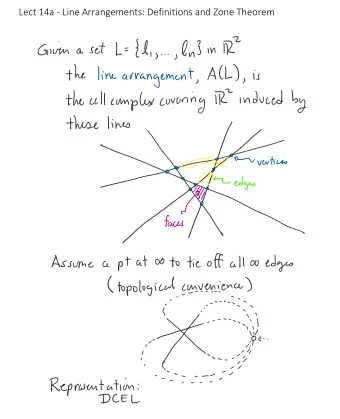
balinski s theorem and regularity of line arrangements
play

Balinskis theorem and Regularity of Line Arrangements Bruno - PowerPoint PPT Presentation

Oct 29, 2023 •426 likes •2.37k views

Balinskis theorem and Regularity of Line Arrangements Bruno Benedetti (University of Miami) CombinaTeXas, May 7, 2016 Bruno Benedetti (University of Miami) Balinskis theorem and Regularity of Line Arrangements Joint work with Bruno

  1. Plan for today Part I. Many Classes of Dual Graphs. Part II. Some Algebraic Machinery. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  2. Plan for today Part I. Many Classes of Dual Graphs. Part II. Some Algebraic Machinery. Part III. (time permitting) Arrangements of Curves. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  3. Many Classes of Dual graphs Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  4. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  5. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  6. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  7. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Of (equidimensional) subspace arrangements or algebraic varieties : Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  8. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Of (equidimensional) subspace arrangements or algebraic varieties : Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  9. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Of (equidimensional) subspace arrangements or algebraic varieties : Vertices correspond to the irreducible components C 1 , . . . , C s . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  10. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Of (equidimensional) subspace arrangements or algebraic varieties : Vertices correspond to the irreducible components C 1 , . . . , C s . (Equidimensional means, they all have same dimension.) Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  11. Many Classes of Dual graphs Of (pure) simplicial complexes (e.g. polytope boundaries): Of arrangements of lines or of curves : (There’s also a “dual multigraph” model, keeping track on how many intersections, with multiple edges/loops.) Of (equidimensional) subspace arrangements or algebraic varieties : Vertices correspond to the irreducible components C 1 , . . . , C s . (Equidimensional means, they all have same dimension.) We put an edge between two distinct vertices, if and only if the corresponding components intersect in dimension one less. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  12. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  13. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  14. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. picture from mathwarehouse.com Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  15. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. picture from mathwarehouse.com NOTE: If you started with an arrangement of hyperplanes (or of linear subspaces), you end up with an arrangement of lines . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  16. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. picture from mathwarehouse.com NOTE: If you started with an arrangement of hyperplanes (or of linear subspaces), you end up with an arrangement of lines .   � dual graphs dual graphs �    = of subspace of lines arr’ts  Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  17. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. picture from mathwarehouse.com NOTE: If you started with an arrangement of hyperplanes (or of linear subspaces), you end up with an arrangement of lines .   � dual graphs � dual graphs dual graphs � �    = ⊂ of subspace of lines of curves arr’ts  Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  18. Dual graphs of curves = dual graphs of varieties By intersecting a d -dimensional object in P n with a generic hyperplane, we get an object in P n − 1 with dimension d − 1, and same dual graph! This way you can always reduce yourself to an (algebraic) curve arrangement with same dual graph. picture from mathwarehouse.com NOTE: If you started with an arrangement of hyperplanes (or of linear subspaces), you end up with an arrangement of lines .   � dual graphs � dual graphs � dual graphs dual graphs � � �    = ⊂ = . of subspace of lines of curves of varieties arr’ts  Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  19. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  20. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  21. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  22. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  23. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? There are only two chances (possibly coinciding): either it’s the line through P and Q , Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  24. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? There are only two chances (possibly coinciding): either it’s the line through P and Q , or it’s the line of intersection of the planes p ∩ q Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  25. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? There are only two chances (possibly coinciding): either it’s the line through P and Q , or it’s the line of intersection of the planes p ∩ q So two options!, not three. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  26. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? There are only two chances (possibly coinciding): either it’s the line through P and Q , or it’s the line of intersection of the planes p ∩ q So two options!, not three. So some of the three lines r 5 , r 6 , r 7 have to coincide. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  27. Not all graphs are dual to a line arrangement Attention!, graphs like G 0 = { 12 , 34 } ∪ { 15 , 25 , 35 , 45 } ∪ { 16 , 26 , 36 , 46 } ∪ { 17 , 27 , 37 , 47 } are not dual to any Euclidean line arrangement! Try drawing it. Let P = r 1 ∩ r 2 and let Q = r 3 ∩ r 4 . Let p be the plane containing r 1 ∪ r 2 , and let q be the plane containing r 3 ∪ r 4 . How can a line meet all four r 1 , r 2 , r 3 , r 4 ? There are only two chances (possibly coinciding): either it’s the line through P and Q , or it’s the line of intersection of the planes p ∩ q So two options!, not three. So some of the three lines r 5 , r 6 , r 7 have to coincide. a contradiction Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  28. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  29. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  30. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  31. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  32. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  33. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 ...and then blowup “unwanted intersection points”. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  34. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 ...and then blowup “unwanted intersection points”. So, Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  35. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 ...and then blowup “unwanted intersection points”. So, � dual graphs � dual graphs � dual graphs � � � � = = all graphs . of lines of curves of varieties Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  36. Dual graphs of curves = all graphs Kollar 2012: every graph is dual to some arrangement of curves . IDEA: Start realizing K n with n random lines in P 2 ... Kyle Jenkins, Urban Geometry #296, acrilic on canvas, 2010 ...and then blowup “unwanted intersection points”. So, � dual graphs � dual graphs � dual graphs � � � � = = all graphs . of lines of curves of varieties It remains to see how dual graphs of simpl. complexes fit the hierarchy. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  37. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  38. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  39. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  40. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  41. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  42. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  43. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  44. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  45. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional ⇒ edge! Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  46. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional ⇒ edge! The intersection of the first and third component is { x : x 4 = x 5 = x 6 = x 1 = x 2 = 0 } , Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  47. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional ⇒ edge! The intersection of the first and third component is { x : x 4 = x 5 = x 6 = x 1 = x 2 = 0 } , which is 1-dim. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  48. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional ⇒ edge! The intersection of the first and third component is { x : x 4 = x 5 = x 6 = x 1 = x 2 = 0 } , which is 1-dim. ⇒ no edge! Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  49. Simplicial Complexes, Seen as Varieties (Stanley-Reisner) Definition by example: Consider the simplicial complex ∆ below. I ∆ := ( x 4 , x 5 , x 6 ) ∩ ( x 1 , x 5 , x 6 ) ∩ ( x 1 , x 2 , x 6 ) ∩ ( x 1 , x 2 , x 3 ) . (Prime ideals ↔ facets; each prime ideal just lists the variables corresponding to vertices that are not in that facet). � x 4 = 0 � x 1 = 0 � x 1 = 0 � x 1 = 0 � � � � V ( I ∆ ) = ∪ ∪ ∪ x 5 = 0 x 5 = 0 x 2 = 0 x 2 = 0 x 6 = 0 x 6 = 0 x 6 = 0 x 3 = 0 Dual graph of V ( I ∆ )? The intersection of the first 2 components is { x : x 4 = x 5 = x 6 = x 1 = 0 } , which is 2-dimensional ⇒ edge! The intersection of the first and third component is { x : x 4 = x 5 = x 6 = x 1 = x 2 = 0 } , which is 1-dim. ⇒ no edge! ... So dual graph of V ( I ∆ ) is same of ∆. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  50. { dual graphs of complexes } ⊂ { dual graphs of lines } Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  51. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  52. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  53. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  54. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . A special variety (a coordinate subspace arrangement): Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  55. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . A special variety (a coordinate subspace arrangement): So when we do generic hyperplane sections, we get an arrangement of lines . Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  56. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . A special variety (a coordinate subspace arrangement): So when we do generic hyperplane sections, we get an arrangement of lines . FACT For any simplicial complex ∆, the dual graphs of ∆ and of V ( I ∆ ) are the same. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  57. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . A special variety (a coordinate subspace arrangement): So when we do generic hyperplane sections, we get an arrangement of lines . FACT For any simplicial complex ∆, the dual graphs of ∆ and of V ( I ∆ ) are the same. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  58. { dual graphs of complexes } ⊂ { dual graphs of lines } Stanley-Reisner : simplicial complexes on n vertices are in bijection with radical monomial ideals in C [ x 1 , . . . , x n ]. Zariski : radical ideals I in C [ x 1 , . . . , x n ] are in bijection with algebraic objects V ( I ) in A n . Composing the two, from any complex ∆ we get an algebraic object V ( I ∆ ) ⊂ A n . A special variety (a coordinate subspace arrangement): So when we do generic hyperplane sections, we get an arrangement of lines . FACT For any simplicial complex ∆, the dual graphs of ∆ and of V ( I ∆ ) are the same. � dual graphs � � � dual graphs of ⊂ . This implies simplicial complexes of lines (Graphs like { 12 , 13 , 15 , 23 , 24 , 34 , 45 } show the containment is strict.) Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  59. Conclusions of Part I. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  60. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  61. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  62. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  63. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  64. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Example Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  65. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Example (from 3 slides forward - ignore obscure words for now) For any ( d − 1)-sphere ∆, the variety V ( I ∆ ) is an arithmetically Gorenstein subspace arrangement of Castelnuovo–Mumford regularity d + 1. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  66. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Example (from 3 slides forward - ignore obscure words for now) For any ( d − 1)-sphere ∆, the variety V ( I ∆ ) is an arithmetically Gorenstein subspace arrangement of Castelnuovo–Mumford regularity d + 1. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  67. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Example (from 3 slides forward - ignore obscure words for now) For any ( d − 1)-sphere ∆, the variety V ( I ∆ ) is an arithmetically Gorenstein subspace arrangement of Castelnuovo–Mumford regularity d + 1. Maybe elementary facts like “the dual graph of any ( d − 1)-sphere ∆ is d -connected” (Klee-Balinski) can be proven with algebraic methods? Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  68. Conclusions of Part I. The notion of “dual graph” can be lifted from simplicial complexes to algebraic varieties. (We can restrict ourselves to dimension one if you wish, so curves or lines.) Statements on graphs of polytopes (like Balinski’s theorem, or diameter bounds), might extend to this more general world: Example (from 3 slides forward - ignore obscure words for now) For any ( d − 1)-sphere ∆, the variety V ( I ∆ ) is an arithmetically Gorenstein subspace arrangement of Castelnuovo–Mumford regularity d + 1. Maybe elementary facts like “the dual graph of any ( d − 1)-sphere ∆ is d -connected” (Klee-Balinski) can be proven with algebraic methods? Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  69. Part II. The Algebraic Machinery (sketch). Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  70. Complete intersections Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  71. Complete intersections Linear algebra : every k -dimensional subspace X of P n can be described with exactly n − k linear equations. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  72. Complete intersections Linear algebra : every k -dimensional subspace X of P n can be described with exactly n − k linear equations. Non-Linear algebra : The best we can say about a variety X ⊂ P n , is that we need at least n − k (polynomial) equations. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  73. Complete intersections Linear algebra : every k -dimensional subspace X of P n can be described with exactly n − k linear equations. Non-Linear algebra : The best we can say about a variety X ⊂ P n , is that we need at least n − k (polynomial) equations. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

  74. Complete intersections Linear algebra : every k -dimensional subspace X of P n can be described with exactly n − k linear equations. Non-Linear algebra : The best we can say about a variety X ⊂ P n , is that we need at least n − k (polynomial) equations. Complete intersections are the varieties for which “=” holds. The ”twisted cubic” ( s 3 , s 2 t , st 2 , t 3 ) of P 3 is not a complete intersection: one needs at least three (hyper)surfaces to cut it out. Bruno Benedetti (University of Miami) Balinski’s theorem and Regularity of Line Arrangements

Recommend

Lect 14a - Line Arrangements: Definitions and Zone Theorem Lect 14b - Line Arrangements:

Lect 14a - Line Arrangements: Definitions and Zone Theorem Lect 14b - Line Arrangements:

Lect 14a - Line Arrangements: Definitions and Zone Theorem Lect 14b - Line Arrangements: Definitions and Zone Theorem Lect 14c - Line Arrangements: Definitions and Zone Theorem

432 views • 5 slides
On the Regularity Method for Hypergraphs Mathias Schacht October 2004 Regularity Method for

On the Regularity Method for Hypergraphs Mathias Schacht October 2004 Regularity Method for

On the Regularity Method for Hypergraphs Mathias Schacht October 2004 Regularity Method for Hypergraphs 1 Outline 1 Density Theorems Szemerdis Density Theorem Density Theorems of Furstenberg and Katznelson Regularity Method for

1.01k views • 83 slides
Partition regularity of some quadratic equations Joint work with N. Frantzikinakis Ergodic Theory

Partition regularity of some quadratic equations Joint work with N. Frantzikinakis Ergodic Theory

Partition regularity of some quadratic equations Joint work with N. Frantzikinakis Ergodic Theory with Connections to Arithmetic Heraklion, June 3, 2013 I A Theorem of partition regularity Definition. A family of finite subsets of N is

675 views • 32 slides
Standard Cell Layout Regularity and Pin Access Optimization Considering Middle-of-Line Wei Ye 1

Standard Cell Layout Regularity and Pin Access Optimization Considering Middle-of-Line Wei Ye 1

Standard Cell Layout Regularity and Pin Access Optimization Considering Middle-of-Line Wei Ye 1 Bei Yu 1 Yong-Chan Ban 2 Lars Liebmann 3 David Z. Pan 1 1 ECE Department, University of Texas at Austin, Austin, TX, USA 2 System IC R&D Lab, LG

824 views • 47 slides
Lecture 2: Existence, uniqueness, and regularity in the Lipschitz case Habib Ammari Department

Lecture 2: Existence, uniqueness, and regularity in the Lipschitz case Habib Ammari Department

Lecture 2: Existence, uniqueness, and regularity in the Lipschitz case Habib Ammari Department of Mathematics, ETH Z urich Numerical methods for ODEs Habib Ammari Existence, uniqueness, and regularity Banach fixed point theorem

837 views • 37 slides
Todays exercises 5.17: Football Pools 5.18: Cells of Line and Hyperplane Arrangements

Todays exercises 5.17: Football Pools 5.18: Cells of Line and Hyperplane Arrangements

Exercise Session 9 03.05.2016 slide 1 Todays exercises 5.17: Football Pools 5.18: Cells of Line and Hyperplane Arrangements Inclass: PPZ on the formula F 6.1: Harmonic vs. Geometric Mean 6.2: Many j -isolated Satisfying

385 views • 13 slides
Proving Non-regularity Question: Is every language a regular language? No. Each DFA M can be

Proving Non-regularity Question: Is every language a regular language? No. Each DFA M can be

Algorithms & Models of Computation Regular Languages, DFA s, NFA s CS/ECE 374, Fall 2017 Theorem Languages accepted by DFA s, NFA s, and regular expressions are the same. Proving Non-regularity Question: Is every language a regular language?

803 views • 6 slides
Alex Suciu Northeastern University Summer Conference on Hyperplane Arrangements Hokkaido

Alex Suciu Northeastern University Summer Conference on Hyperplane Arrangements Hokkaido

O N THE TOPOLOGY OF LINE ARRANGEMENTS Alex Suciu Northeastern University Summer Conference on Hyperplane Arrangements Hokkaido University, Sapporo, Japan August 9, 2016 C OMPLEMENTS OF HYPERPLANE ARRANGMENTS An arrangement of hyperplanes is

276 views • 27 slides
Regularity-Constrained Floorplanning Regularity Constrained Floorplanning for Multi-Core

Regularity-Constrained Floorplanning Regularity Constrained Floorplanning for Multi-Core

Regularity-Constrained Floorplanning Regularity Constrained Floorplanning for Multi-Core Processors Ning Xu Xi Chen Jiang Hu Department of ECE College of CST T exas A&M University Wuhan University of T echnology 1 Outline Outline

544 views • 36 slides
Regularity Comparativism about Mass in Newtonian Gravity Niels C.M. Martens PSA 2016 Slides

Regularity Comparativism about Mass in Newtonian Gravity Niels C.M. Martens PSA 2016 Slides

Regularity Comparativism about Mass in Newtonian Gravity Niels C.M. Martens PSA 2016 Slides available at http://users.ox.ac.uk/~corp2044 5 Nov 2016 Outline The Regularity Approach 1 Empiricism about laws of nature Regularity Relationalism

430 views • 28 slides
Applications of the Sparse Regularity Lemma Y. Kohayakawa (Emory and So Paulo) Extremal

Applications of the Sparse Regularity Lemma Y. Kohayakawa (Emory and So Paulo) Extremal

Applications of the Sparse Regularity Lemma Y. Kohayakawa (Emory and So Paulo) Extremal Combinatorics II DIMACS 2004 Tools fo sparse regularity 1 Szemerdis regularity lemma 1. Works very well for large, dense graphs: n -vertex graphs

680 views • 64 slides
Alex Suciu Northeastern University Workshop on Configuration Spaces Il Palazzone di Cortona

Alex Suciu Northeastern University Workshop on Configuration Spaces Il Palazzone di Cortona

T OPOLOGY OF LINE ARRANGEMENTS Alex Suciu Northeastern University Workshop on Configuration Spaces Il Palazzone di Cortona September 1, 2014 A LEX S UCIU (N ORTHEASTERN ) T OPOLOGY OF LINE ARRANGEMENTS C ORTONA , S EPT . 2014 1 / 24 O UTLINE I

469 views • 24 slides
The midpoint theorem states that a line joining midpoints of two sides of a triangle are parallel

The midpoint theorem states that a line joining midpoints of two sides of a triangle are parallel

D AY 68 D ILATION AS A RESULT OF MIDPOINT THEOREM I NTRODUCTION We have seen that a line passing joining midpoints of two sides of a triangle is parallel to the third side and it is half the length of the third side. A part of this idea of

1.64k views • 13 slides
Pseudofinite groups and tame arithmetic regularity Gabriel Conant Notre Dame 23 July 2018 Logic

Pseudofinite groups and tame arithmetic regularity Gabriel Conant Notre Dame 23 July 2018 Logic

Pseudofinite groups and tame arithmetic regularity Gabriel Conant Notre Dame 23 July 2018 Logic Colloquium University of Udine Regularity Szemer edis Regularity Lemma (1976): Any sufficiently large finite graph can be nontrivially

991 views • 61 slides
Efficient arithmetic regularity and removal lemmas for induced bipartite patterns Yufei Zhao

Efficient arithmetic regularity and removal lemmas for induced bipartite patterns Yufei Zhao

Efficient arithmetic regularity and removal lemmas for induced bipartite patterns Yufei Zhao (MIT) Joint work with Noga Alon (Princeton) and Jacob Fox (Stanford) April 22, 2018 1 Szemer edis graph regularity lemma Graph regularity lemma

577 views • 41 slides
Computational Geometry Lecture 11: Arrangements and Duality Computational Geometry Lecture 11:

Computational Geometry Lecture 11: Arrangements and Duality Computational Geometry Lecture 11:

Introduction Duality Arrangements Arrangements and Duality Computational Geometry Lecture 11: Arrangements and Duality Computational Geometry Lecture 11: Arrangements and Duality Introduction Duality Arrangements Three Points on a Line

1.01k views • 65 slides
Co-Management Arrangements in Healthcare: Compliance in Hospital-Physician Arrangements THURSDAY,

Co-Management Arrangements in Healthcare: Compliance in Hospital-Physician Arrangements THURSDAY,

Presenting a live 90-minute webinar with interactive Q&A Co-Management Arrangements in Healthcare: Compliance in Hospital-Physician Arrangements THURSDAY, DECEMBER 7, 2017 1pm Eastern | 12pm Central | 11am Mountain | 10am

753 views • 61 slides
Regularity of powers of edge ideals Huy Ti H Tulane University Joint with Selvi Beyarslan

Regularity of powers of edge ideals Huy Ti H Tulane University Joint with Selvi Beyarslan

Regularity of powers of edge ideals Huy Ti H Tulane University Joint with Selvi Beyarslan and Trn Nam Trung Huy Ti H Regularity of powers of edge ideals Problem and Motivation 1 Asymptotic linearity of regularity Stabilization

1.09k views • 31 slides
Regularity Comparativism about Mass in Newtonian Gravity Niels Martens Society for the

Regularity Comparativism about Mass in Newtonian Gravity Niels Martens Society for the

Regularity Comparativism about Mass in Newtonian Gravity Niels Martens Society for the Metaphysics of Science 2 nd annual conference, Geneva Slides available at http://users.ox.ac.uk/~corp2044 16 Sept 2016 Outline The Regularity Approach 1

587 views • 27 slides
Preservation of prox-regularity Florent Nacry 1 Based on a joint work with Samir Adly and Lionel

Preservation of prox-regularity Florent Nacry 1 Based on a joint work with Samir Adly and Lionel

Notation and preliminaries Preservation of prox-regularity: state of the art Prox-regularity and generalized equations Future works and references Preservation of prox-regularity Florent Nacry 1 Based on a joint work with Samir Adly and Lionel

457 views • 44 slides
Straight line rolling of an ellipsoid on a plane and the Chasles theorem Yuri F edorov, UPC,

Straight line rolling of an ellipsoid on a plane and the Chasles theorem Yuri F edorov, UPC,

Straight line rolling of an ellipsoid on a plane and the Chasles theorem Yuri F edorov, UPC, Barcelona (still Spain) X 2 + X 2 + X 2 R 3 = ( X 1 , X 2 , X 3 ) 1 1 3 Q = = 1 A 1 A 2 A 3 n No slip no twist The

388 views • 11 slides
Combinatorics and topology of toric arrangements II. Topology of arrangements in the complex torus

Combinatorics and topology of toric arrangements II. Topology of arrangements in the complex torus

Combinatorics and topology of toric arrangements II. Topology of arrangements in the complex torus (An invitation to combinatorial algebraic topology) Emanuele Delucchi (SNSF / Universit e de Fribourg) Toblach/Dobbiaco February 23, 2017

543 views • 42 slides
Bilateral arrangements Bilateral arrangements Challenges and opportunities for Challenges and

Bilateral arrangements Bilateral arrangements Challenges and opportunities for Challenges and

Bilateral arrangements Bilateral arrangements Challenges and opportunities for Challenges and opportunities for Croatia Croatia Currently 3 arrangements 13-14 November 2008 EU/US FDA EU/Japan MHLW-PMDA Transatlantic

94 views • 5 slides
Regularity results for optimal patterns in the branched transportation problem Alessio Brancolini

Regularity results for optimal patterns in the branched transportation problem Alessio Brancolini

The functional The landscape function Fractal regularity Regularity results for optimal patterns in the branched transportation problem Alessio Brancolini Joint works with Prof. Solimini Politecnico di Bari Optimization Days, Ancona, June

306 views • 18 slides

More recommend