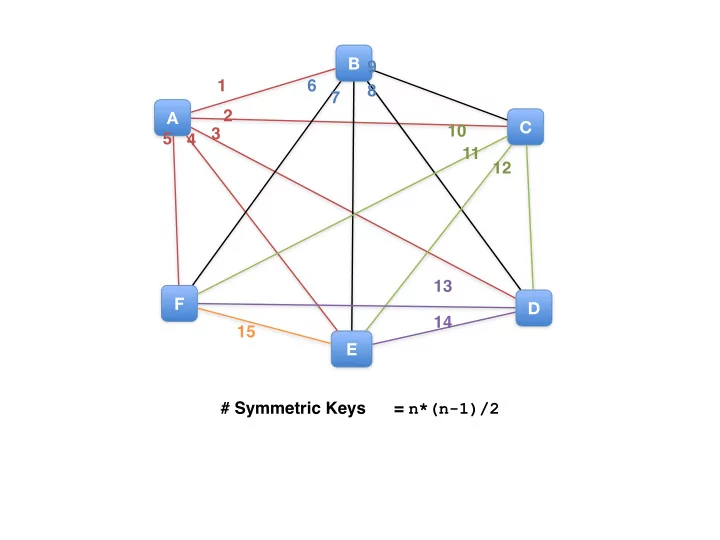
B 9 1 6 8 7 A 2 C 10 3 5 4 11 12 13 F D 14 15 E # - PowerPoint PPT Presentation

B 9 1 6 8 7 A 2 C 10 3 5 4 11 12 13 F D 14 15 E # Symmetric Keys = n*(n-1)/2

# Symmetric Keys = n*(n-1)/2 # Public/Private Keys = 2 n public private B 9 1 6 8 7 A 2 C 10 3 public private 5 4 public private 11 12 13 F D 14 public private 15 public private E public private

RSA • Chose two random large prime numbers p & q (of equal length is best) 
 • Compute their product n = pq • Randomly choose an encryption key e : 
 e and (p-1)(q-1) are relatively prime (gcd=1) 
 • Calculate the decryption key d : 
 d = e -1 mod ((p-1)(q-1)) (-1 is modular inverse)

RSA encryption Split up the message into blocks less than n c i = m ie mod n Decryption is similar d i = c id mod n

RSA Example p=47 , q=71, n=pq=3337 Choose e : no factors common with 
 𝞆 =(p-1)(q-1) = 46*70 = 3220 randomly choose e to be 3 Then d=3 -1 mod 3337 = 2147

RSA Example (continued) • Message M H E L L O W O R L D ! 72 69 76 76 79 32 87 79 82 76 68 33 • Treat each letter as a block 
 72 69 76 76 79 32 87 79 82 76 68 33 m1 m2 m3 m4 m5 m6 m7 m8 m9 ma mb mc 
 • Encrypt each block 
 72 3 mod 3337 = 2841 = c 1 2841 1483 1829 1829 2500 2735 c1 c2 c3 c4 c5 c6 1114 2500 763 1829 754 2567 c7 c8 c9 ca cb cc Using Matlab™ or https://defuse.ca/big-number-calculator.htm

RSA Example (continued) • Ciphertest C 2841 1483 1829 1829 2500 2735 1114 2500 763 1829 754 2567 • Treat each number as a block 
 • Decrypt each block 
 2841 2147 mod 3337 = 72 = m 1 Using matlab™ or 
 https://defuse.ca/big-number-calculator.htm

As long as factoring is hard … m e mod N ≡ ? is easy ? e mod N ≡ c is hard! RSA is secure

Symmetric Key Signatures Alice uses k A to encrypt the document going to Bob and sends it to Trent 1 Trent decrypts the document with k A 2 Trent appends a statement that he received it from Alice 3 Trent encrypts the bundle with k B 4 Trent sends the encrypted bundle to Bob 5 Bob decrypts the bundle with k B , and can read the message and Trent’s certification 6

Public Key Signatures Alice encrypts the document with her private key 1 Alice sends the encrypted (signed) document to Bob 2 Bob decrypts the document with Alice’s public key 3

Cryptographic Hashes SHA-1(” The red fox jumps over the blue dog”) = 0x12d6ae1b4a5c1c99ba6e4d60c22c42abe56d0e08b3111222880606 a12a9b5aab 
 SHA-1(” The red foy jumps over the blue dog”) = 
 0xc1b02530f4cf6867e606abebf1bd05bc608d27db147a4589934404e6 7c19911c 
 SHA-1(” The red fxo jumps over the blue dog”) = 
 0x9a9bed6ca1a3333989b7c7b849f99ba2da685494865201ee3729d3 ad09560c03 fox=0x66 6F 78 foy=0x66 6F 79 fxo=66 78 6F

Public Key Signature with Timestamp Alice adds a timestamp to the document 1 Alice encrypts the document with her private key 2 Alice sends the encrypted (signed) document to Bob 3 Bob takes the check to the bank 4 Bank decrypts the document with Alice’s public key 5 Bank stores the check information and the timestamp in a database 6 If Bob tries to deposit the check again, its information will match the database 7

Multiple Signatures Alice signs a hash of the document 1 Bob signs a hash of the document 2 Bob sends his signature to Alice 3 Alice sends the document, her signature, and Bob’s signature to Carol 4 Carol can verify both signatures 5

Digital signatures • a file to be signed • proof that the file has not been altered • indication of who applied the signature • validation that the signature is authentic 
 (i.e., belongs to the signer) • connection of the signature to the file

Digital Signatures and Encryption (to protect the file) Alice encrypts the file with her private key * 1 Alice computes a hash of the encrypted file 2 Alice encrypts the hash with her private key 3 Alice sends the encrypted message, encrypted hash, and her identity to Bob, 4 encrypted with his public key Bob decrypts the entire message with his private key 5 Bob obtains the public key associated with the identity in the message 6 Bob decrypts the encrypted hash with Alice’s public key 2 Bob calculates a hash of the encrypted message and verifies that it matches the 3 hash in the signature Bob decrypts the encrypted message with Alice’s public key 4 * - if the message is large, a symmetric cipher and key should be used

Digital Signature Optimizations Message is Message is not secret secret encrypt the message Message is encrypt only the hash AND the hash with small with Private Key Private Key encrypt message with Message is encrypt only the hash symmetric key and large with Private Key hash with public key

Digital Signatures and Encryption typical notation Alice Bob S A (M) E B (S A (M) ) D B (E B (S A (M))) = S A (M) V A (S A (M)) = M

Needham-Schroeder Protocol

MITM Attack on N-S

The Fix Note that Alice obtained Bob’s public key by sending his identity B to a Certificate Authority. Note that Alice obtained Bob’s public key by sending his identity B to a Certificate Authority. Alice also verifies his identity B.