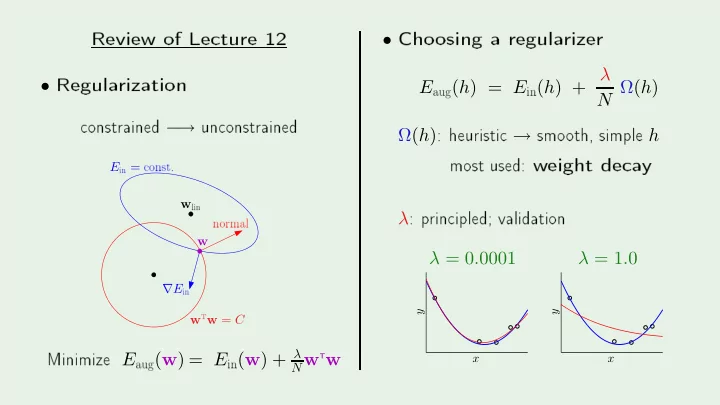
aug h e in h onstrained
play

aug ( h ) = E in ( h ) + onstrained unonstrained : heuristi - PowerPoint PPT Presentation

Jun 16, 2023 •120 likes •357 views

Review of Leture 12 Cho osing a regula rizer Regula rization aug ( h ) = E in ( h ) + onstrained unonstrained : heuristi smo oth, simple h N ( h ) E most used: w eight dea y onst. in = ( h )

  1. Review of Le ture 12 Cho osing a regula rizer Regula rization aug ( h ) = E in ( h ) + λ • onstrained − un onstrained : heuristi → smo oth, simple h • N Ω( h ) E most used: w eight de a y onst. in = → Ω( h ) lin : p rin ipled; validation E normal w λ in PSfrag repla ements PSfrag repla ements w λ = 0 . 0001 λ = 1 . 0 t w = C -1 -1 -0.5 -0.5 ∇ E T w 0 0 0.5 0.5 Minimize E aug ( w ) = E in ( w ) + λ 1 1 0 0 0.5 0.5 y y 1 1 w 1.5 1.5 2 2 x x N w

  2. Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 13 : V alidation Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST T uesda y , Ma y 15, 2012 •

  3. Outline The validation set • Mo del sele tion • Cross validation • Creato r: Y aser Abu-Mostafa - LFD Le ture 13 2/22 M � A L

  4. V alidation versus regula rization In one fo rm o r another, over�t p enalt y out ( h ) = E in ( h ) + Regula rization: E over�t p enalt y out ( h ) = E in ( h ) + regula rization estimates this quantit y E V alidation: � �� � over�t p enalt y out ( h ) in ( h ) + validation estimates this quantit y = E E Creato r: Y aser Abu-Mostafa - LFD Le ture 13 3/22 � �� � M � A L

  5. Analyzing the estimate On out-of-sample p oint ( x , y ) , the erro r is e ( h ( x ) , y ) Squa red erro r: Bina ry erro r: � � 2 h ( x ) − y � h ( x ) � = y � e ( h ( x ) , y ) out ( h ) va r e ( h ( x ) , y ) � � = E E � � = σ 2 Creato r: Y aser Abu-Mostafa - LFD Le ture 13 4/22 M � A L

  6. F rom a p oint to a set e ( h ( x k ) , y k ) On a validation set ( x 1 , y 1 ) , · · · , ( x K , y K ) , the erro r is E v al ( h ) = 1 K � K e ( h ( x k ) , y k ) v al ( h ) out ( h ) k =1 K 1 � � � � � = = E E E E K va r va r e ( h ( x k ) , y k ) v al ( h ) k =1 K = σ 2 1 � � � � � = E K 2 v al ( h ) = E out ( h ) ± O K k =1 � 1 � Creato r: Y aser Abu-Mostafa - LFD Le ture 13 5/22 √ E K M � A L

  7. PSfrag repla ements is tak en out of N 20 Given the data set D = ( x 1 , y 1 ) , · · · , ( x N , y N ) K 40 60 p oints validation p oints training 80 train v al 100 120 → N − K → K : Small K bad estimate � �� � � �� � 0.05 D D out r 0.1 Erro La rge K ? � � 0.15 1 = ⇒ O √ e ted K 0.2 E in Exp Numb er of Data P oints, N − K 0.25 = ⇒ E Creato r: Y aser Abu-Mostafa - LFD Le ture 13 6/22 ← − K M � A L

  8. is put ba k into N train ∪ D v al K train D − → D D ↓ ↓ ↓ ( N ) train N − K v al N K D La rge K = bad estimate! ( N − K ) v al = E v al ( g − ) g − D = ⇒ D = ⇒ g Rule of Thumb: ⇒ E D g v al ( g ) ( K ) Creato r: Y aser Abu-Mostafa - LFD Le ture 13 7/22 K = N 5 g E M � A L

  9. Why `validation' is used to mak e lea rning hoi es v al top 3.5 If an estimate of E a�e ts lea rning: out D 3 the set is no longer a test set! 2.5 2 It b e omes a validation set Error 1.5 E 1 Early stopping out 0.5 E Creato r: Y aser Abu-Mostafa - LFD Le ture 13 8/22 in 0 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 Epochs bottom M � A L

  10. What's the di�eren e? T est set is unbiased; validation set has optimisti bias T w o hyp otheses and h 2 with out ( h 1 ) = E out ( h 2 ) = 0 . 5 Erro r estimates e 1 and e 2 unifo rm on [0 , 1] h 1 E Pi k with e = min( e 1 , e 2 ) e ) < 0 . 5 optimisti bias h ∈ { h 1 , h 2 } E ( Creato r: Y aser Abu-Mostafa - LFD Le ture 13 9/22 M � A L

  11. Outline The validation set • Mo del sele tion • Cross validation • Creato r: Y aser Abu-Mostafa - LFD Le ture 13 10/22 M � A L

  12. Using D mo re than on e v al mo dels H 1 , . . . , H M train Use D to lea rn g − fo r ea h mo del train M v al H 1 H 2 · · · H M Evaluate g − using D : D v al pi k the b est m g 1 g 2 · · · gM v al ( g − ( H m ∗ , Em ∗ ) D m Pi k mo del m = m ∗ with smallest E m E 1 E 2 · · · EM | {z } E m = E m ); m = 1 , . . . , M D Creato r: Y aser Abu-Mostafa - LFD Le ture 13 11/22 gm ∗ M � A L

  13. PSfrag repla ements The bias 0.8 W e sele ted the mo del H m ∗ using D v al 0.7 is a biased estimate of E v al ( g − out ( g − 0.6 Illustration: sele ting b et w een 2 mo dels out m ∗ ) m ∗ ) E 0.5 r Erro v al 5 15 25 � � e ted g − E m ∗ Exp � � g − V alidation Set Size, K E m ∗ Creato r: Y aser Abu-Mostafa - LFD Le ture 13 12/22 M � A L

  14. Ho w mu h bias F o r M mo dels: H 1 , . . . , H M is used fo r �training� on the �nalists mo del : v al val = { g − m } D Ba k to Ho e�ding and V C! 1 , g − 2 , . . . , g − H out ( g − v al ( g − �� � regula rization λ ea rly-stopping T ln M m ∗ ) ≤ E m ∗ ) + O E K Creato r: Y aser Abu-Mostafa - LFD Le ture 13 13/22 M � A L

  15. Data ontamination Erro r estimates: E in , E test , E v al Contamination: Optimisti (de eptive) bias in estimating E out T raining set: totally ontaminated V alidation set: slightly ontaminated T est set: totally ` lean' Creato r: Y aser Abu-Mostafa - LFD Le ture 13 14/22 M � A L

  16. Outline The validation set • Mo del sele tion • Cross validation • Creato r: Y aser Abu-Mostafa - LFD Le ture 13 15/22 M � A L

  17. The dilemma ab out K The follo wing hain of reasoning: out ( g ) ≈ out ( g − ) ≈ v al ( g − ) (small K ) (la rge K ) E E E highlights the dilemma in sele ting K : Can w e have K b oth small and la rge? Creato r: Y aser Abu-Mostafa - LFD Le ture 13 16/22 M � A L

  18. Leave one out p oints fo r training, and 1 p oint fo r validation! ���� N − 1 Final hyp othesis lea rned from D n is g − D n = ( x 1 , y 1 ) , . . . , ( x n − 1 , y n − 1 ) , ( x n , y n ) , ( x n +1 , y n +1 ) , . . . , ( x N , y N ) e n = E e ( g − v al ( g − n ross validation erro r: e n v = 1 n ) = n ( x n ) , y n ) N � E Creato r: Y aser Abu-Mostafa - LFD Le ture 13 17/22 N n =1 M � A L

  19. PSfrag repla ements PSfrag repla ements PSfrag repla ements Illustration of ross validation 0.1 0.1 0.2 0.2 0.3 0.3 0.1 0.4 0.4 0.2 0.5 0.5 0.3 0.6 0.6 0.4 0.7 0.7 e 3 e 2 0.5 0.8 0.8 0.6 0.9 0.9 0.7 0.65 0.65 0.8 0.7 0.7 0.9 0.75 0.75 -0.2 0.8 0.8 e 1 0 0.85 0.85 0.2 0.9 0.9 0.4 0.95 0.95 0.6 1 1 y y y 0.8 1.05 1.05 1 1.1 1.1 1.2 1.15 1.15 e 1 + e 2 + e 3 ) v = 1 x x x Creato r: Y aser Abu-Mostafa - LFD Le ture 13 18/22 3 ( E M � A L

  20. PSfrag repla ements PSfrag repla ements PSfrag repla ements Mo del sele tion using CV 0.1 0.1 0.2 0.2 0.3 0.3 0.1 0.4 0.4 0.2 0.5 0.5 0.3 0.6 0.6 0.4 0.7 0.7 e 3 e 2 0.5 0.8 0.8 0.6 0.9 0.9 Linea r: 0.7 0.65 0.65 0.8 0.7 0.7 PSfrag repla ements 0.9 PSfrag repla ements 0.75 PSfrag repla ements 0.75 -0.2 0.8 0.8 e 1 0 0.85 0.85 0.2 0.9 0.9 0.4 0.95 0.95 0.6 1 1 y y y 0.8 1.05 1.05 1 1.1 1.1 0.1 0.1 0.1 1.2 1.15 1.15 0.2 0.2 0.2 0.3 0.3 0.3 0.4 0.4 0.4 0.5 0.5 0.5 e 3 0.6 0.6 0.6 e 2 x x x e 1 0.7 0.7 0.7 Constant: 0.8 0.8 0.8 0.9 0.9 0.9 0.7 0.7 0.7 0.75 0.75 0.75 0.8 0.8 0.8 0.85 0.85 0.85 0.9 0.9 0.9 0.95 0.95 0.95 y y y 1 1 1 1.05 1.05 1.05 Creato r: Y aser Abu-Mostafa - LFD Le ture 13 19/22 1.1 1.1 1.1 x x x M � A L

  21. PSfrag repla ements PSfrag repla ements Not Cross validation in a tion Digits lassi� ation task Di�erent erro rs 0.03 0.1 0.2 0.02 0.3 out 0.4 -8 -7 0.01 -6 v E -5 Not 1 Symmetry -4 -3 A verage Intensit y 5 10 15 20 -2 E in -1 0 # F eatures Used 1 E Creato r: Y aser Abu-Mostafa - LFD Le ture 13 20/22 (1 , x 1 , x 2 ) → (1 , x 1 , x 2 , x 2 1 , x 1 x 2 , x 2 2 , x 3 1 , x 2 1 x 2 , . . . , x 5 1 , x 4 1 x 2 , x 3 1 x 2 2 , x 2 1 x 3 2 , x 1 x 4 2 , x 5 2 ) M � A L

  22. PSfrag repla ements 0.05 0.1 0.15 0.2 0.25 0.3 0.35 PSfrag repla ements 0.4 The result -5 -4.5 without validation with validation -4 -3.5 0.05 0.1 -3 0.15 0.2 -2.5 0.25 -2 0.3 0.35 -1.5 -5 Symmetry Symmetry -4 -1 -3 A verage Intensit y -2 -0.5 -1 0 0 A verage Intensit y in = 0% out = 2 . 5% in = 0 . 8% out = 1 . 5% Creato r: Y aser Abu-Mostafa - LFD Le ture 13 21/22 E E E E M � A L

  23. Leave mo re than one out Leave one out: training sessions on N − 1 p oints ea h Mo re p oints fo r validation? N train v alidate train D z }| { D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 training sessions on N − K p oints ea h 10-fold ross validation: K = N N K Creato r: Y aser Abu-Mostafa - LFD Le ture 13 22/22 10 M � A L

More recommend