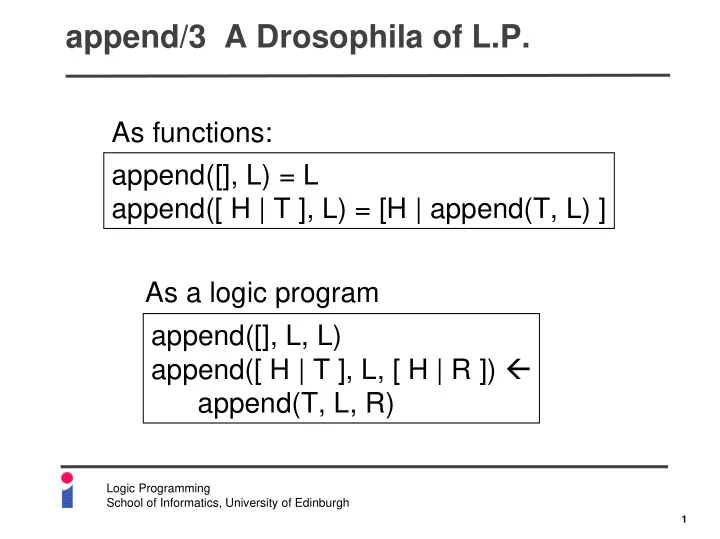
append/3 A Drosophila of L.P. As functions: append([], L) = L - PowerPoint PPT Presentation

append/3 A Drosophila of L.P. As functions: append([], L) = L append([ H | T ], L) = [H | append(T, L) ] As a logic program append([], L, L) append([ H | T ], L, [ H | R ]) � append(T, L, R) Logic Programming School of Informatics, University of Edinburgh 1

append/3 A Drosophila of L.P. append([], L, L) append([ H | T ], L, [ H | R ]) � append(T, L, R) Goals: Results: X = [a,b,c,d,e] append([a,b,c], [d,e], X) append(X, [d,e], [a,b,c,d,e]) X = [a,b,c] append([a,b,c], X, [a,b,c,d,e]) X = [d,e] append(X, Y, [a,b,c,d,e]) X = [], Y = [a,b,c,d,e] ; X = [a], Y = [b,c,d,e]; etc append([a,b,c], X, Y) Y = [a,b,c | X ] Logic Programming School of Informatics, University of Edinburgh 2

Introduction to Negation as Failure In Prolog the goal \+ G succeeds if no instance of G can be found by Prolog’s proof mechanism; otherwise it fails. Goals: Results: Given: yes \+ (p(1), r(1)). p(X) :- q(X). no \+ (p(2), r(2)). q(1). no \+ p(X). q(2). yes \+ (p(X), s(X)). r(2). s(3). Logic Programming School of Informatics, University of Edinburgh 3

Generating a Set of Results setof(X, Goal, Set) generates the set, S, of instances of X generated by exhaustively satisfying the given Goal. Goals: Results: Given: S = [1,2] setof(X, p(X), S). p(X) :- q(X). S = [2] setof(X, (p(X), r(X)), S). q(1). S = [1,2,3] setof(X, (p(X) ; s(X)), S). q(2). setof(X, (p(X), s(X)), S). no r(2). s(3). Logic Programming School of Informatics, University of Edinburgh 4

Building Larger Definitions: Map Colouring The four colour theorem says that any 2- dimensional map can be coloured, with no bordering country sharing the same colour, using only four different colours. Logic Programming School of Informatics, University of Edinburgh 5

A Logic Program Requirement Define a predicate colour_countries(X) that generates in X a list of terms [c(S,C),…], where S is a country and C is one of four colours. The predicate must be able to generate each combination of countries and colours satisfying the four-colour theorem but no combinations that do not satisfy the theorem. An example behaviour is: | ?- colour_countries(X). X=[c(austria,red), c(belgium,green), c(denmark,yellow), c(france,red), c(germany,blue), c(italy,blue), c(netherlands,yellow), c(portugal,blue), c(spain,yellow), c(switzerland,yellow)] Logic Programming School of Informatics, University of Edinburgh 6

A Representation of a Map ngb(portugal, [spain]). ngb(spain, [portugal,france]). ngb(france, [spain,belgium,switzerland,germany,italy]). ngb(belgium, [france,germany,netherlands]). ngb(netherlands, [belgium,germany]). ngb(germany, [netherlands,belgium,france,switzerland,austria,denmark]). ngb(switzerland, [france,germany,austria,italy]). ngb(austria, [germany,switzerland,italy]). ngb(italy, [france,switzerland,austria]). ngb(denmark, [germany]). Note this is not the only representation we could have used. The art is to describe the salient and essential details of the problem, and no more than this. Logic Programming School of Informatics, University of Edinburgh 7

Generating Individual Neighbours neighbour(Country, Country1) :- ngb(Country, Neighbours), member(Country1, Neighbours). member(X, [ X | _ ]). member(X, [ _ | T ]):- member(X, T). Logic Programming School of Informatics, University of Edinburgh 8

Colouring the Countries colour_countries(Colours) :- setof(c(Country,_), X^ngb(Country,X), Colours), colours(Colours). colours([]). colours([ c(Country,Colour) | Rest ]) :- colours(Rest), member(Colour, [yellow,blue,red,green]), \+ ( member(c(Country1,Colour), Rest), neighbour(Country, Country1) ). Logic Programming School of Informatics, University of Edinburgh 9