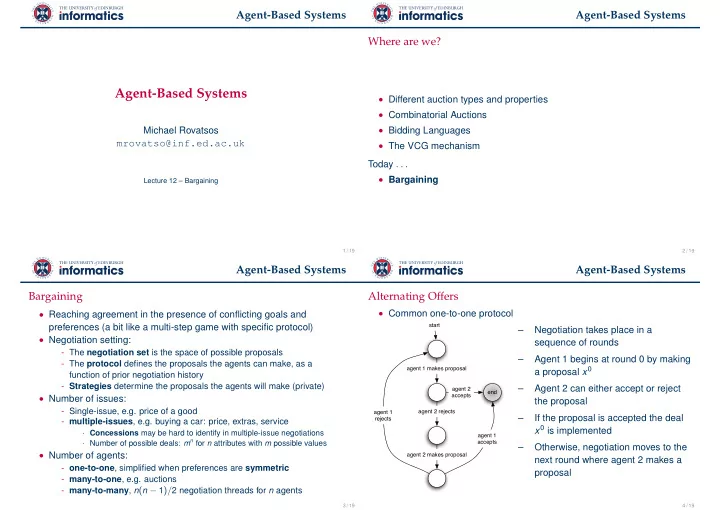

Agent-Based Systems Agent-Based Systems Where are we? Agent-Based Systems • Different auction types and properties • Combinatorial Auctions Michael Rovatsos • Bidding Languages mrovatso@inf.ed.ac.uk • The VCG mechanism Today . . . • Bargaining Lecture 12 – Bargaining 1 / 19 2 / 19 Agent-Based Systems Agent-Based Systems Bargaining Alternating Offers • Common one-to-one protocol • Reaching agreement in the presence of conflicting goals and preferences (a bit like a multi-step game with specific protocol) start – Negotiation takes place in a • Negotiation setting: sequence of rounds - The negotiation set is the space of possible proposals – Agent 1 begins at round 0 by making - The protocol defines the proposals the agents can make, as a agent 1 makes proposal a proposal x 0 function of prior negotiation history - Strategies determine the proposals the agents will make (private) – Agent 2 can either accept or reject agent 2 end accepts • Number of issues: the proposal - Single-issue, e.g. price of a good agent 1 agent 2 rejects – If the proposal is accepted the deal rejects - multiple-issues , e.g. buying a car: price, extras, service x 0 is implemented · Concessions may be hard to identify in multiple-issue negotiations agent 1 · Number of possible deals: m n for n attributes with m possible values accepts – Otherwise, negotiation moves to the • Number of agents: agent 2 makes proposal next round where agent 2 makes a - one-to-one , simplified when preferences are symmetric proposal - many-to-one , e.g. auctions - many-to-many , n ( n − 1 ) / 2 negotiation threads for n agents 3 / 19 4 / 19
Agent-Based Systems Agent-Based Systems Scenario: Dividing the Pie Negotiation Rounds • The ultimatum game : a single negotiation round - Suppose that player 1 proposes to get all the pie, i.e. ( 1 , 0 ) - Player 2 will have to agree to avoid getting the conflict deal Θ • Scenario: Dividing the pie - Player 1 has all the power - There is some resource whose value is 1 • Two rounds of negotiation - The resource can be divided into two parts, such as 1 The values of each part must be between 0 and 1 - Agent 1 makes a proposal in the first round 2 The sum of the values of the parts sum to 1 - Player 2 can reject and turn the game into an ultimatum - A proposal is a pair ( x , 1 − x ) (agent 1 gets x , agent 2 gets 1 − x ) • If the number of rounds is fixed, whoever moves last gets all the pie - The negotiation set is: { ( x , 1 − x ) : 0 ≤ x ≤ 1 } • If there are no bounds on the number of rounds: • Some assumptions: - Suppose agent 1’s strategy is: propose ( 1 , 0 ) , reject any other offer - Disagreement is the worst outcome, we call this the conflict deal Θ - If agent 2 rejects the proposal, the agents will never reach - Agents seek to maximise utility agreement (the conflict deal is enacted) - Agent 2 will have to accept to avoid Θ - Infinite set of Nash equilibrium outcomes (of course agent 2 must understand the situation, e.g. given access to agent 1’s strategy) 5 / 19 6 / 19 Agent-Based Systems Agent-Based Systems Time Negotiation Decision Functions • Non-strategic approach, does not depend on how other’s behave • Additional assumption: Time is valuable (agents prefer outcome x • Agents use a time-dependent decision function to determine what at time t 1 over outcome x at time t 2 if t 2 > t 1 ) proposal they should make • Model agent i ’s patience using discount factor δ i (0 ≤ δ i ≤ 1) • Boulware strategy: exponentially decay offers to reserve price the value of slice x at time 0 is δ 0 i x = x • Conceder strategy: make concessions early, do not concede much the value of slice x at time 1 is δ 1 i x = δ i x as negotiation progresses the value of slice x at time 2 is δ 2 i x = ( δ i δ i ) x Price Price • More patient players (larger δ i ) have more power Conceder 1.0 1.0 • Games with two rounds of negotiation 0.8 Boulware 0.8 - The best possible outcome for agent 2 in the second round is δ 2 0.6 0.6 - If agent 1 initially proposes ( 1 − δ 2 , δ 2 ) , agent 2 can do no better than accept 0.4 0.4 Conceder • Games with no bounds on the number of rounds Boulware 0.2 0.2 - Agent 1 proposes what agent 2 can enforce in the second round 1 − δ 1 δ 2 , agent 2 gets δ 2 ( 1 − δ 1 ) 1 − δ 2 0.2 0.4 0.6 0.8 1.0 Time 0.2 0.4 0.6 0.8 1.0 Time - Agent 1 gets 1 − δ 1 δ 2 Seller Buyer 7 / 19 8 / 19
Agent-Based Systems Agent-Based Systems Task-oriented domains (I) Task-Oriented Domains (II) • A task-oriented domain (TOD) is a triple � T , Ag , c � with - T a finite set of tasks, Ag a set of agents, and • Utility represents how much agent has to gain from the deal - c : 2 T → R + function describing cost of executing any set of tasks • If no agreement is reached, conflict deal is Θ = � T 1 , T 2 � (symmetric for all agents) • A deal δ 1 dominates another deal δ 2 (denoted δ 1 ≻ δ 2 ) iff • We assume that c ( ∅ ) = 0, and that c is monotonic i.e. 1 Deal δ 1 is at least as good as δ 2 for every agent: T 1 , T 2 ⊆ T ∧ T 1 ⊆ T 2 ⇒ c ( T 1 ) ≤ c ( T 2 ) ∀ i ∈ { 1 , 2 } , utility i ( δ 1 ) ≥ utility i ( δ 2 ) • An encounter in a TOD is a collection � T 1 , . . . , T n � such that each 2 Deal δ 1 is better for some agent than δ 2 : T i ⊆ T is executed by agent i ∈ Ag ∃ i ∈ { 1 , 2 } , utility i ( δ 1 ) > utility i ( δ 2 ) • Below, we only consider one-to-one negotiation scenarios where a • If δ 1 is not dominated by any other δ 2 , then δ is Pareto optimal deal is a pair δ = � D 1 , D 2 � such that D 1 ∪ D 2 = T 1 ∪ T 2 • A deal is individually rational if it weakly dominates (i.e. is at least • Agent i will execute D i in a deal with as good as) the conflict deal Θ - cost i ( δ ) = c ( D i ) , and - utility i ( δ ) = c ( T i ) − cost i ( δ ) 9 / 19 10 / 19 Agent-Based Systems Agent-Based Systems Task-Oriented Domains (III) The monotonic concession protocol this oval deals on this line from delimits the space B to C are Pareto optimal, • Start with simultaneous deals proposed by both agents and of all possible deals hence in the negotiation set proceed in rounds • Agreement reached if B - utility 1 ( δ 2 ) ≥ utility 1 ( δ 1 ) or - utility 2 ( δ 1 ) ≥ utility 2 ( δ 2 ) • If both proposals match or exceed other’s offer, outcome is chosen A E at random between δ 1 and δ 2 C • If no agreement, in round u + 1 agents are not allowed to make deals less preferred by other agent than proposal made in round u • If no proposals are made, negotiation terminates with outcome Θ D the conflict • Protocol verifiable and guaranteed to terminate, but not necessarily deal efficient Negotiation set contains individually rational and Pareto optimal deals 11 / 19 12 / 19
Agent-Based Systems Agent-Based Systems The Zeuthen strategy The Zeuthen strategy (II) • Agent with smaller value of risk should concede on round t • The above protocol doesn’t describe when and how much to concede • Concession should be just good enough but of course this is • Intuitively, agents will be more willing to risk conflict if difference inefficient, smallest concession that changes balance of risk between current proposal and conflict deal is low • Problem if agents have equal risk: we have to flip a coin, otherwise • Model agent i ’s willingness to risk conflict at round t as one of them could defect (and conflict would occur) • Looking at our protocol criteria: i = utility lost by conceding and accepting j ’s offer risk t - Protocol terminates, doesn’t always succeed, simplicity? (too many utility lost by not conceding and causing conflict deals), Zeuthen strategy is Nash, no central authority needed, • Formally, we can calculate risk as a value between 0 and 1 individual rationality (in case of agreement), Pareto optimality • Zlotkin/Rosenschein also analysed a number of scenarios in which � if utility i ( δ t i ) = 0 1 agents lie about their tasks: risk t i = utility i ( δ t i ) − utility i ( δ t j ) otherwise - Phantom/decoy tasks: advantage for deceitful agent utility i ( δ t i ) - Hidden tasks: agents may benefit from hiding tasks (!) 13 / 19 14 / 19 Agent-Based Systems Agent-Based Systems Bargaining for Resource Allocation (I) Bargaining for Resource Allocation (II) • A resource allocation setting is a tuple � Ag , Z , v 1 , . . . , v n � , • A pay-off vector p = � p 1 , p 2 , . . . , p n � is a tuple of side payments - Agents Ag = { 1 , . . . , n } such that � n - Resources Z = { z 1 , . . . , z m } i = 1 p i = 0 - Valuation functions v i : 2 Z → R p � , where Z , Z ′ ∈ alloc ( Z , Ag ) are distinct • A deal is a triple � Z , Z ′ , ¯ • An allocation Z 1 , . . . , Z n is a partition of resources over the agents allocations and ¯ p is a payoff vector • Negotiating a change from P i to Q i ( P i , Q i ∈ Z and P i � = Q i ) will • � Z , Z ′ , ¯ p � is individually rational if v i ( Z ′ i ) − p i > v i ( Z ) for each lead to i ∈ Ag , p i is allowed to be 0 if Z i = Z ′ i - v i ( P i ) < v i ( P i ) , • Pareto optimal: every other allocation that makes some agents - v i ( P i ) = v i ( P i ) or strictly better off makers some other agent strictly worse off - v i ( P i ) > v i ( P i ) • Agents can make side payments as compensations 15 / 19 16 / 19
Recommend
More recommend