Abundance profiles The suffix ome refers to a totality of some sort - PDF document

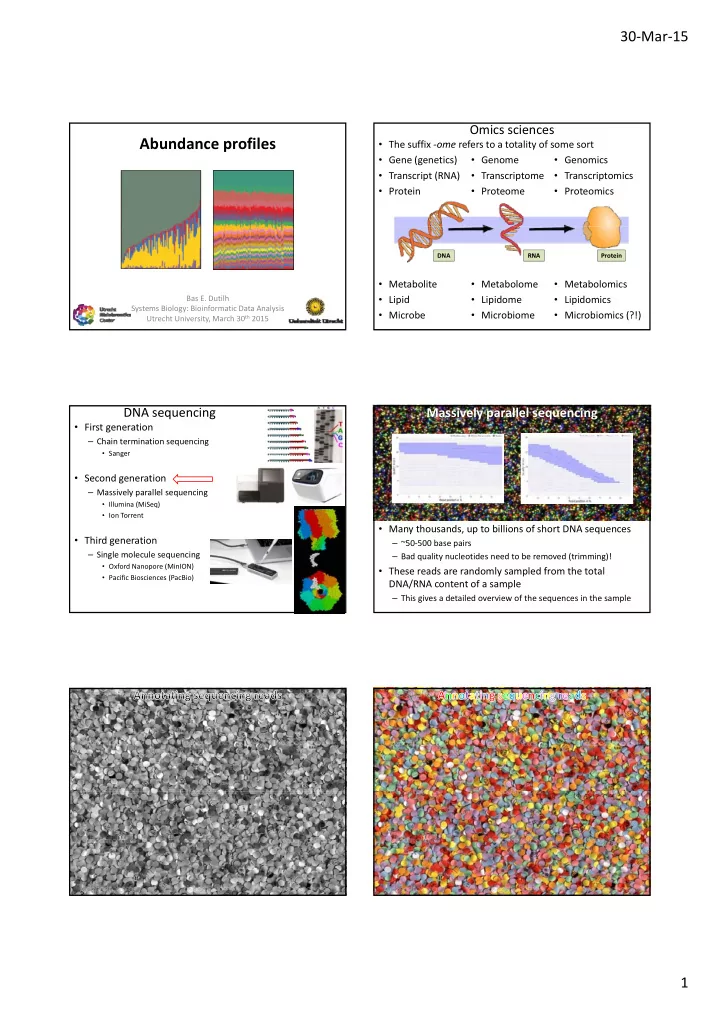
30 ‐ Mar ‐ 15 Omics sciences Abundance profiles • The suffix ‐ ome refers to a totality of some sort • Gene (genetics) • Genome • Genomics • Transcript (RNA) • Transcriptome • Transcriptomics • Protein • Proteome • Proteomics DNA RNA Protein • Metabolite • Metabolome • Metabolomics Bas E. Dutilh • Lipid • Lipidome • Lipidomics Systems Biology: Bioinformatic Data Analysis • Microbe • Microbiome • Microbiomics (?!) Utrecht University, March 30 th 2015 DNA sequencing Massively parallel sequencing • First generation – Chain termination sequencing • Sanger • Second generation – Massively parallel sequencing • Illumina (MiSeq) • Ion Torrent • Many thousands, up to billions of short DNA sequences • Third generation – ~50 ‐ 500 base pairs – Single molecule sequencing – Bad quality nucleotides need to be removed (trimming)! • Oxford Nanopore (MinION) • These reads are randomly sampled from the total • Pacific Biosciences (PacBio) DNA/RNA content of a sample – This gives a detailed overview of the sequences in the sample 1

30 ‐ Mar ‐ 15 Who/what is present in the sample? Micro ‐ arrays • Last week we discussed how to annotate these • Micro ‐ arrays are another way of identifying sequences in a sequencing reads by aligning to a reference database sample – Fast, heuristic similarity search programs are used for this – Micro ‐ arrays can only identify previously known sequences – That is why DNA sequencing is now the standard • The result is an overview of the genes/functions/microbes and their relative abundances in the sequencing reads A micro ‐ array is a glass slide that contains pieces of DNA with a known sequence q High g Many reads Many reads Low Few reads Functions Species Green/red labeled sample or taxa sequences hydridize to the sequences on the micro ‐ array These results are just lists of numbers DNA: human microbiome • Which bacterial phyla are present in different • DNA: metagenome: list of all microbial human body sites? genes and organisms and relative • Which metabolic functions do they encode? abundances in an environment • Can we use this to understand the differences – Micro ‐ organisms play important between people? roles in ecology and thus in health • RNA: transcriptome lists all genes and their relative expression values in a cell/tissue expression values in a cell/tissue – Gene expression is important for phenotype • Protein: proteome lists all proteins in a sample and their relative abundances – Proteins perform most of the functions in a cell • A list of numbers is also known as a a x multidimensional vector, for example: a y a z Different healthy people DNA: microbiome studies RNA: discover cancer biomarker genes • Can we improve the prognosis for cancer patients by analyzing their gene expression profile? Jack Gilbert Jack Gilbert Up ‐ regulated genes Argonne National Lab Argonne National Lab Down ‐ regulated genes ts Patient Genes 2

30 ‐ Mar ‐ 15 RNA: heat shock response • How do Saccharomyces cerevisiae (yeast) genes respond to increased growth temperature? Up ‐ regulated genes Down ‐ regulated genes s Gene 5 15 30 60 Time (minutes) High ‐ throughput sequencing Scaling • Same organism, different tissues or body sites • When analyzing transcriptome data, we find that the RNA expression of gene A consists of: – For example: brain versus liver, mouth versus gut – 4,000 reads in a healthy tissue sample • Same tissue, same organism – 10,000 reads in a tumor sample – For example: treatment versus control, tumor versus healthy • Can we conclude that gene A is over ‐ expressed in cancer? • Same tissue, different organisms – The total volume of the transcriptomic datasets are: – For example: wildtype versus knock ‐ out/transgenic/mutant, • 80 000 sequencing reads from the healthy tissue 80,000 sequencing reads from the healthy tissue comparing monozygotic twin pairs comparing monozygotic twin pairs • 500,000 sequencing reads from the tumor • Time course experiments 4,000 10,000 – For example: effect of a treatment, development of a tissue, Healthy: = 0.05 Tumor: = 0.02 80,000 500,000 response of microbiota to environmental change – No, the gene is actually expressed much lower in the tumor Comparing read counts Gene expression in time • To compare samples, we need to: • Normalized and scaled gene expression values – Scale the numbers so that they add up to 1 – For example, expression of genes in aging Arabidopsis leaves • This accounts for differences in the sample size (total number of reads) 0. 25 • Divide each number by the total number of reads – Normalize numbers so that they are (close to) normally 0. 20 distributed pression Gene 1 • This is important in many statistical tests 0 0. 15 15 • Biological data are often logarithmically distributed – if so, you could take Bi l i l d t ft l ith i ll di t ib t d if ld t k Gene 2 G 2 Abundance/Exp the logarithm of the number of reads to normalize 0. 10 Gene 3 5 0.0 0 Value 1 2 3 4 5 6 7 8 9 10 Time/environments/samples… …or leaves… Log (value) 3

30 ‐ Mar ‐ 15 Microbial abundance in time Research setup 1. Design experimental conditions and sampling strategy • Normalized and scaled microbial abundance values – For example, presence of pathogens on rotting Arabidopsis leaves 2. Extract DNA/RNA/protein 0. 25 3. Sequence nucleotides or proteins 20 0. pression 4. Quality control of sequencing reads or peptides Microbe 1 0 0. 15 15 Microbe 2 Mi b 2 Abundance/Exp 5. Annotate (e.g. align reads to database) and count 0. 10 Microbe 3 6. Normalize and scale the counts 0.0 5 7. Compare samples, clustering (next lecture) 0 1 2 3 4 5 6 7 8 9 10 8. Interpret results and perform verification experiments Time/environments/samples… …or leaves… Quantifying similarity between vectors Distance matrices • Based on these measurements, which genes/microbes/etc are more • Distance matrix • Similarity matrix inverse similar to each other? • Abundance/expression levels 0 x y 1 1 ‐ x 1 ‐ y 0. 25 are most similar between and • Abundance/expression patterns inverse x 0 z 1 ‐ x 1 1 ‐ z 0. 20 are most similar between and pression y z 0 1 ‐ y 1 ‐ z 1 0. 0 15 15 • We can use a distance measure W di t Abundance/Exp to quantify the (dis ‐ )similarity 10 between the lists 0. – Many different distance distance = 1 ‐ similarity measures exist 0.0 5 0 1 2 3 4 5 6 7 8 9 10 Time/Environments/Samples Manhattan distance (levels) Euclidean distance (levels) d AB = (X A – X B ) 2 + (Y A – Y B ) 2 2 2 d AB = |X A – X B | + |Y A – Y B | = + d AB d AB 0 0 0.265 0.799 0.103 0.253 0 0 0.265 0.534 0.103 0.178 0 0 0.799 0.534 0.253 0.178 Example: Example: • • d 2 = (0.20 – 0.15) 2 + d = |0.20 – 0.15| + ( A (Y A – Y B ) 2 (Y A – Y B ) 2 ( A B ) B ) (0.17 – 0.15) 2 + |0.17 – 0.15| + (X A – X B ) 2 (X A – X B ) 2 (0.16 – 0.16) 2 + |0.16 – 0.16| + (0.20 – 0.15) 2 + |0.20 – 0.15| + 1 0.20 0.15 0.12 1 0.20 0.15 0.12 (0.20 – 0.16) 2 + |0.20 – 0.16| + 2 0.17 0.15 0.09 2 0.17 0.15 0.09 3 (0.17 – 0.16) 2 + 3 0.16 0.16 0.08 0.16 0.16 0.08 |0.17 – 0.16| + 4 (0.16 – 0.15) 2 + 4 0.20 0.15 0.11 0.20 0.15 0.11 |0.16 – 0.15| + 5 5 0.20 0.16 0.12 (0.20 – 0.15) 2 + 0.20 0.16 0.12 |0.20 – 0.15| + 6 6 0.17 0.16 0.10 0.17 0.16 0.10 (0.18 – 0.16) 2 + |0.18 – 0.16| + 7 7 0.16 0.15 0.08 0.16 0.15 0.08 (0.16 – 0.15) 2 = 0.0105  d = 0.103 |0.16 – 0.15| = 0.265 8 0.20 0.15 0.12 8 0.20 0.15 0.12 d = 0.799 d = 0.253 9 0.18 0.16 0.11 9 0.18 0.16 0.11 d = 0.534 d = 0.178 10 0.16 0.15 0.08 10 0.16 0.15 0.08 4

30 ‐ Mar ‐ 15 Comparing patterns instead of distances Compare patterns instead of distances • Correlation can be used to quantify the similarity between • Correlation can be used to quantify 1 0 ‐ 0.35 1.35 ‐ 0.16 1.16 patterns the similarity between patterns 1 ‐ 0.35 1.35 0 0.97 0.03 0.25 0. 25 0.25 1 0.20 0.15 0.12 0 1 ‐ 0.16 1.16 0.03 0.97 2 0.17 0.15 0.09 r = ‐ 0.35 3 0.16 0.16 0.08 0.2 r = ‐ 0.35 20 0. 0.2 4 ression pression 0.20 0.15 0.11 Low correlation Little correlation ession 5 0.20 0.16 0.12 6 0.15 0.17 0.16 0.10 0 0. 15 15 0 15 0.15 Abundance/Exp Abundance/Exp Abundance/Expr 7 0.16 0.15 0.08 8 0.20 0.15 0.12 0.1 9 0.18 0.16 0.11 0. 10 0.1 10 0.16 0.15 0.08 0.05 0.0 5 0.05 r = 0.97 r = 0.97 1 0 ‐ 0.35 1.35 ‐ 0.16 1.16 High correlation Positive correlation 0 0 0 0 1 ‐ 0.35 1.35 0.97 0.03 0 0.05 0.1 0.15 0.2 0.25 1 2 3 4 5 6 7 8 9 10 0 0.05 0.1 0.15 0.2 0.25 Abundance/Expression of Time/Environments/Samples Abundance/Expression of 0 1 ‐ 0.16 1.16 0.03 0.97 5