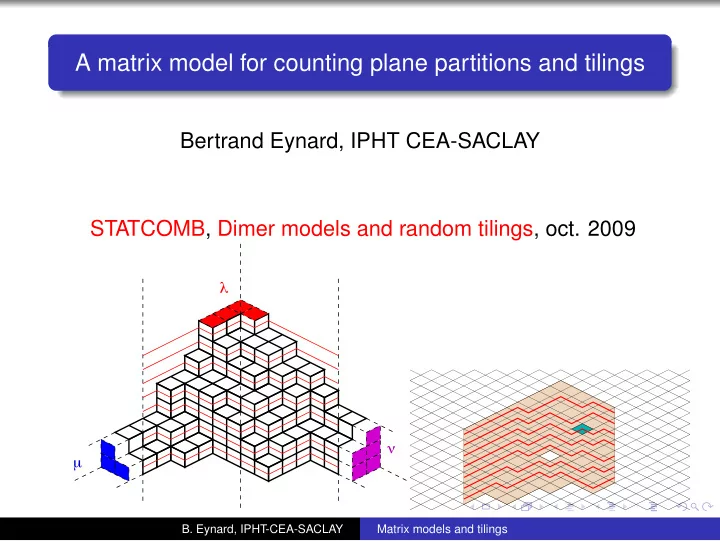
A matrix model for counting plane partitions and tilings Bertrand - PowerPoint PPT Presentation

A matrix model for counting plane partitions and tilings Bertrand Eynard, IPHT CEA-SACLAY STATCOMB, Dimer models and random tilings, oct. 2009 " ! µ B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction cusp: Pearcey edge: Airy tangent edge: Hermit bulk: sine In all those limits: statistics of cubes ∼ random matrix eigenvalues statistics. B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Introduction cusp: Pearcey edge: Airy tangent edge: Hermit bulk: sine Question: is there a matrix model whose eigenvalues statistics = statistics of cubes ? before any limit ? B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Outline Outline: Plane partitions, tilings and TASEP Rewriting as a matrix integral Tools available for matrix models Orthogonal polynomials, determinantal formulae, integrability, loop equations. topological expansion of the matrix model Large size asymptotics, liquid region. Examples Tiling the hexagon, the cardioid, TSSCPPs. Conclusion B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Plane partitions • Plane partition, with 3 given boundaries λ, µ, ν : Left Right N N ! µ " N ! " µ B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Plane partitions • Plane partition, with 3 given boundaries λ, µ, ν : Left Right N N ! µ " N ! " µ B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Plane partitions • Plane partition, with 3 given boundaries λ, µ, ν : Left Right N N ! µ " N ! " µ B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Plane partitions • Plane partition, with 3 given boundaries λ, µ, ν : t " ! ! = N self avoiding particles moving in a given region of the Rhombus lattice. B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Plane partitions • Plane partition, with 3 given boundaries λ, µ, ν : t ! h 7 h 6 h 5 h 4 h 3 h 2 " µ h 1 h = N self avoiding particles moving in a given region of the Rhombus lattice. h i ( t ) , i = 1 , . . . , N , h i ( t ) − t h i ( t + 1 ) = h i ( t ) ± 1 2 ∈ Z , 2 , h 1 ( t ) > h 2 ( t ) > h 3 ( t ) > · · · > h N ( t ) . B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Generalization N self avoiding particles moving in a given arbitrary domain D of the Rhombus lattice. h i ( t ) , i = 1 , . . . , N , h i ( t ) − t 2 ∈ Z , h 1 ( t ) > h 2 ( t ) > h 3 ( t ) > · · · > h N ( t ) , h i ( t + 1 ) = h i ( t ) + 1 2 with proba α ( t + 1 2 ) h i ( t + 1 ) = h i ( t ) − 1 2 with proba β ( t + 1 2 ) Possibility of having forbidden places, obliged places, non flat landscape, jumps other than ± 1 2 ,... B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Partition function Left Right N ! N µ " N ! " µ Plane partitions: � q | π | Z N λ , N µ , N ν ( λ, µ, ν ) = π,∂π =( λ,µ,ν ) Example, Mac-Mahon formula N λ = N µ = N ν = ∞ , λ, µ, ν = ∅ : ∞ � � q | π | = ( 1 − q k ) − k = 1 + q + 3 q 2 + 6 q 3 + 13 q 4 + . . . Z = π k = 1 B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Partition function, TASEP Generalization self-avoiding process in a domain D : t max − 1 N � � � e − V t ( h i ( t )) q h i ( t ) Z = t = t min i = 1 h 1 ( t ) > ··· > h N ( t ) � � � � α ( t ′ ) δ h i ( t ′ + 1 2 + β ( t ′ ) δ h i ( t ′ + 1 2 ) , h i ( t ′ − 1 2 )+ 1 2 ) , h i ( t ′ − 1 2 ) − 1 2 t ′ i B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: � i ∞ − i ∞ dr e r ( h ( t + 1 ) − h ( t )) e ± r / 2 . δ ( h ( t + 1 ) − h ( t ) ± 1 2 ) = • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: α δ ( h ( t + 1 ) − h ( t ) + 1 2 ) + β δ ( h ( t + 1 ) − h ( t ) − 1 2 ) = � i ∞ − i ∞ dr e r ( h ( t + 1 ) − h ( t )) ( α e r / 2 + β e − r / 2 ) . • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: α δ ( h ( t + 1 ) − h ( t ) + 1 2 ) + β δ ( h ( t + 1 ) − h ( t ) − 1 2 ) = � i ∞ − i ∞ dr e r ( h ( t + 1 ) − h ( t )) ( α e r / 2 + β e − r / 2 ) . • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) � U ( N ) dU e Tr R U H U † . det ( e r i h j ) = ∆( H )∆( R ) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings

Transformation into a matrix integral Idea: • Gessel-Viennot: � � i paths = � h i ( t ) det ( paths ) . h 1 ( t ) > ··· > h N ( t ) • Fourrier transform δ -functions: α δ ( h ( t + 1 ) − h ( t ) + 1 2 ) + β δ ( h ( t + 1 ) − h ( t ) − 1 2 ) = � i ∞ − i ∞ dr e r ( h ( t + 1 ) − h ( t )) ( α e r / 2 + β e − r / 2 ) . • Harish Chandra-Itzykson-Zuber: H = diag ( h i ) , R = diag ( r i ) det ( e r i ( t + 1 2 ) h j ( t + 1 ) ) = � U ( N ) dU e Tr R ( t + 1 2 ) U H ( t + 1 ) U † , ∆( H ( t + 1 ))∆( R ( t + 1 2 )) det ( e − r i ( t + 1 2 ) h j ( t ) ) = � U ( N ) dU e − Tr R ( t + 1 2 ) U H ( t ) U † . ∆( H ( t ))∆( R ( t + 1 2 )) • Matrices: M ( t ) = U H ( t ) U † , ∆( H ( t )) 2 dH ( t ) dU = dM ( t ) , M ( t ′ ) = U † R ( t ′ ) U , ∆( R ( t ′ )) 2 dR ( t ′ ) dU = d ˜ and ˜ M ( t ′ ) . h i ( t ) = eigenvalues of M ( t ) , and r i ( t ) = eigenvalues of ˜ M ( t ′ ) . → Matrix model B. Eynard, IPHT-CEA-SACLAY Matrix models and tilings