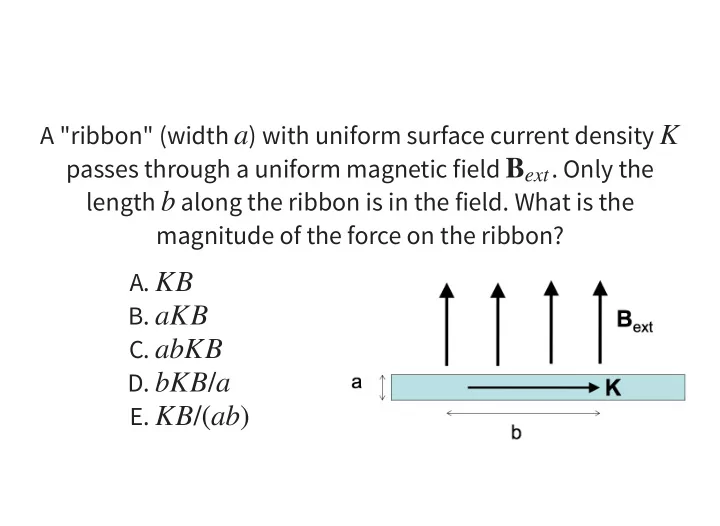

A "ribbon" (width ) with uniform surface current density a K passes through a uniform magnetic field . Only the B ext length along the ribbon is in the field. What is the b magnitude of the force on the ribbon? A. KB B. aKB C. abKB D. bKB / a E. KB /( ab )
To find the magnetic field at P due to a current-carrying B wire we use the Biot-Savart law, ̂ μ 0 d l × ℜ B ( r ) = I ∫ ℜ 2 4 π In the figure, with shown, which purple vector best d l represents ? ℜ
To find the magnetic field at P B due to a current-carrying wire we use the Biot-Savart law, ̂ μ 0 d l × ℜ B ( r ) = I ∫ ℜ 2 4 π What is the direction of the infinitesimal contribution created by current in ? B ( P ) d l A. Up the page B. Directly away from (in the plane of the page) d l C. Into the page D. Out of the page E. Some other direction
̂ What is the magnitude of ? d l × ℜ ℜ 2 A. dl sin θ ℜ 2 B. dl sin θ ℜ 3 C. dl cos θ ℜ 2 D. dl cos θ ℜ 3 E. something else!
̂ What is the value of ? I d l × ℜ ℜ 2 A. I y dx ′ x ′ ) 2 y 2 ] 3/2 z ̂ [( + B. x ′ x ′ I d x ′ ) 2 y 2 ] 3/2 y ̂ [( + C. x ′ x ′ − I d x ′ ) 2 y 2 ] 3/2 y ̂ [( + D. − I y dx ′ x ′ ) 2 y 2 ] 3/2 z ̂ [( + E. Other!
What do you expect for direction of ? How about B ( P ) direction of generated JUST by the segment of d B ( P ) current in red? d l A. in plane of page, ditto for , by red B ( P ) d B ( P ) B. into page, , by red into page B ( P ) d B ( P ) C. into page, , by red out of page B ( P ) d B ( P ) D. complicated, ditto for , by red B ( P ) d B ( P ) E. Something else!!
Recommend
More recommend