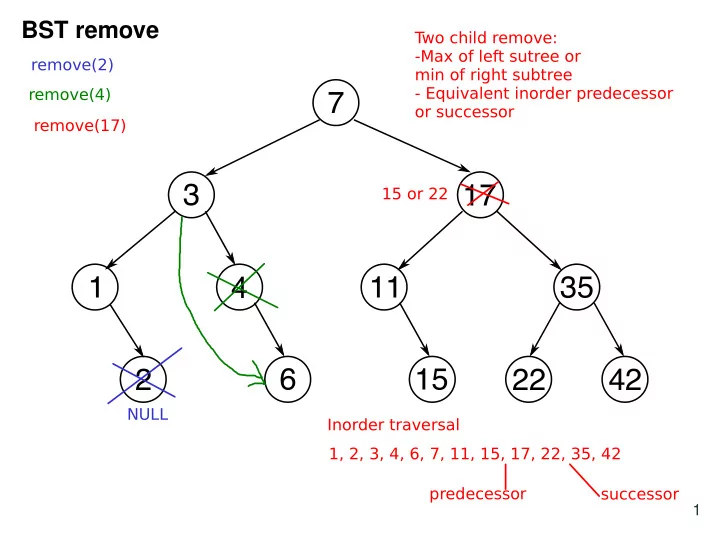

BST remove T wo child remove: -Max of left sutree or remove(2) min of right subtree remove(4) - Equivalent inorder predecessor 7 or successor remove(17) 3 17 15 or 22 1 4 11 35 2 6 15 22 42 NULL Inorder traversal 1, 2, 3, 4, 6, 7, 11, 15, 17, 22, 35, 42 predecessor successor 1
BST remove So we can remove root void remove(Node *& cRoot, const K & key){ Node *& target = find(cRoot, key); 7 doRemoval(target); } 3 17 Get a reference to the pointer to the node to remove. Then we can update node that 1 4 11 35 points to target. 2 6 15 22 42 key By copy L R By reference Node to remove 2
BST remove 7 3 17 1 4 11 35 2 6 15 22 42 void doRemoval(Node *& cRoot){ if ((cRoot->left != NULL) && (cRoot->right != NULL)) T wo 3, 7, 17,25 ____________ChildRemove(cRoot); else ZeroOne 1, 2,4,6,11,15,22,42 ____________ChildRemove(cRoot); } 3
BST remove 7 3 17 35 1 4 11 2 6 15 22 42 void zeroOneChildRemove(Node *& cRoot){ Node * temp = cRoot; if (cRoot->left == NULL) 1 cRoot = cRoot->right; else : What about remove(6)? cRoot = cRoot->left; delete temp; Same code works since right is NULL So we replace the 4->6 with 4->NULL } 4
BST remove 7 15 3 17 35 1 4 11 2 6 15 22 42 rmc remove(17) void twoChildRemove(Node *& cRoot){ 15 Node *& rmc = rightMostChild(croot->left); Overwrite key 17 w/ 15 cRoot->key = rmc->key; Delete old node with key 15 doRemoval(rmc); } 5
BST remove 7 3 17 1 4 11 35 2 6 15 22 42 rightMostChild(17->left) = 15 Node * & 14 void rightMostChild(Node *& cRoot){ if (croot->right == NULL) return cRoot; else : return rightMostChild(cRoot->right); } 6
BST ef fi ciency The runtime of BST algorithms 7 depend on the height ( h ) of the 3 17 tree. 1 4 11 35 The analysis should be in terms of the number of nodes ( n ) the 2 6 15 22 42 tree contains. Reminder: height( T ) is: We need a relationship • between h and n -1 if T is empty • 1 + max { height ( T L ) , heigh ( T R ) } lower bnd f ( n ) h ≥ height(6)=1+max{empty, empty} h g ( n ) upper bnd ≤ =1+-1 =0 7
BST theory What is the maximum number of nodes in a tree of height h ? N(h)=max nodes N ( h ) = 2 h +1 − 1 What is the minimum height of a tree with n nodes? n < 2 h +1 = ⇒ log 2 ( n ) < h + 1 = ⇒ � log 2 ( n ) � ≤ h What is the minimum number Upper bound n-1 is bad if we want to search the tree of nodes in a tree of height h ? h + 1 = ⇒ n ≥ h + 1 What is the maximum height of of a tree with n nodes? a tree of height h ? h ≤ n − 1 Lower bound on h ≥ � log 2 ( n ) � , upper bound on h ≤ n − 1 8
1 BST shape 2 3 7 The height of a BST depends on the order in which data is 4 inserted: 2 6 3 1 5 7 1,2,3,4,5,6,7 vs 4,2,3,6,7,1,5 How many different ways are there to insert n key into a tree? How many ways to order n things? n! Average height, over all arrangements of n keys? log(n) Why? There are more ways to get a "bushy" tree than a "long" tree How many ways to get? 1 How many ways to get? More than 1 4,6,2,1,3,5,7 4,6,2,3,1,5,7 etc 9
BST ef fi ciency BST avg case worst sorted sorted case array list fi nd Θ ( n ) Θ (log 2 ( n )) Θ ( n ) Θ (log 2 ( n )) Binary search Θ ( n ) insert Θ ( n ) Θ (log 2 ( n )) Θ ( n ) shift fi nd Θ (log 2 ( n )) delete Θ ( n ) Θ ( n ) Θ ( n ) shift fi nd Θ ( n ) traverse Θ ( n ) Θ ( n ) Θ ( n ) 10
Tree balance balance = 3 - 6 = -3 x h=3 T L h=6 T R balance(x)=heigh(x.left) - heigh(x.right) If for all nodes x, • balance(x) = 0 then perfectly balanced • |balance(x)| ≤ 1 then tree is “balanced” and height ≤ c log 2 n where c < 2 Are BST s guaranteed to be balanced? No 11 What we want is a way so that insert/remove keep a tree balanced.
Tree rotations 7 3 22 4 35 7 4 17 11 19 32 42 1 3 3 17 Only height of nodes on path to root change 2 0 0 22 4 11 Tree remains a BST 0 19 1 35 Unbalanced 0 0 32 42 Where we are going: - AVL trees are balanced and maintain balance after insertion/removal - We will use rotations to balance the tree after insert/remove 12
Recommend
More recommend