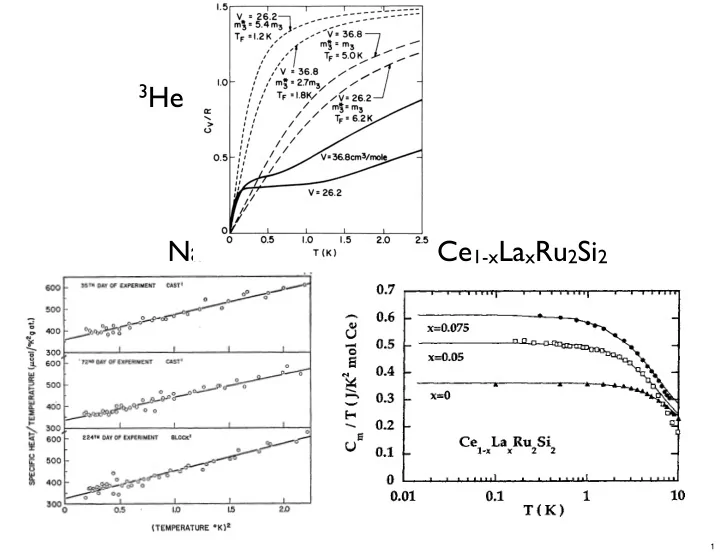
3 he na
play

3 He Na Ce 1-x La x Ru 2 Si 2 1 Rubtsov et al. 05 Gull et al., RMP - PowerPoint PPT Presentation

Sep 30, 2022 •468 likes •589 views

3 He Na Ce 1-x La x Ru 2 Si 2 1 Rubtsov et al. 05 Gull et al., RMP 83 , 349 (2011) b) H 1 [ k ] H 1 [ l ] H 1 [ m ] 0 a) c) 0 0 d) 0 Reasonable expansion order Order controlled through interaction

  1. 3 He Na Ce 1-x La x Ru 2 Si 2 1

  2. Rubtsov et al. ’05 Gull et al., RMP 83 , 349 (2011) b) ˆ ˆ ˆ H 1 [ τ k ] H 1 [ τ l ] H 1 [ τ m ] 0 β a) c) 0 0 β β d) 0 β Reasonable expansion order Order controlled through interaction k / β h ˆ H 1 i 2

  3. 2.5 S/ln(2) 2 4T K χ imp T K γ imp 1.5 R W 1 0.5 0 -6 -4 -2 0 2 4 10 10 10 10 10 10 T/T K 3

  4. 1.2 R(T) Kondo Model 1.0 G(T) Kondo Model R(T)/R(0), G(T)/G(0) R(T) Anderson Model 2 R(T)/R(0)=1 − c(T/T K ) 0.8 Hamann 0.6 0.4 0.2 0.0 − 3 10 − 2 10 − 1 0 1 2 3 4 5 10 10 10 10 10 10 10 T/T K 3

  5. 1.4 1.2 1 0.8 S/ln(2) 0.6 T K χ imp T K γ imp 0.4 R W /(8/3) 0.2 0 -6 -4 -2 0 2 4 10 10 10 10 10 10 T/T K 3

  6. Lattice Lattice A lok ( ω ) /t − 1 DOS 0.15 0.1 0.05 0 10 ε k 5 1 st Brillouin zone ω /t 0 E F ε R M -5 Γ X -10 R X M R Γ k 4

  7. W/2 • Static Néel order: Doubling of unit cell = reduction of BZ = backfolding of bands • New BZ = old Fermi surface E k 0 • Formation of bonding-/ antibonding bands -W/2 -1 0 1 k/ � 5

  8. U = 2W/3 A lok ( ω ) /t − 1 DOS 0.15 0.1 0.05 0 0.4 10 0.3 5 A k ( ω ) /t − 1 ε k ω /t 0 0.2 ε E F R M -5 0.1 -10 Γ X 0 R X M R Γ k Fermi liquid 6

  9. U = 0.87W A lok ( ω ) /t − 1 DOS 0.15 0.1 0.05 0 0.4 10 0.3 5 A k ( ω ) /t − 1 ε k ω /t 0 0.2 ε E F R M -5 0.1 -10 Γ X 0 R X M R Γ k Insulator (no Fermi liquid) 6

  10. 1 real particles quasi-particles n(k) 1 m ∗ 0 Γ k F 1. BZ k 7

  11. Magnetic properties at half filling: 0.8 Kent, TP et al. , ’05 • Calculate staggered susceptibility 0.6 Weiss Heisenberg • Perform finite-size SOPT scaling up to size 32 Staudt T/t 0.4 DMFA Result: DCA • T c (DCA)<T c (DMFT) antiferromagnetic insulator 0.2 DCA • Large U ➫ Heisenberg DMFT „Mott“ model „Slater“ 0 0 5 10 15 20 Interesting: U/t Properties for T<T N ? 8

Recommend

More recommend