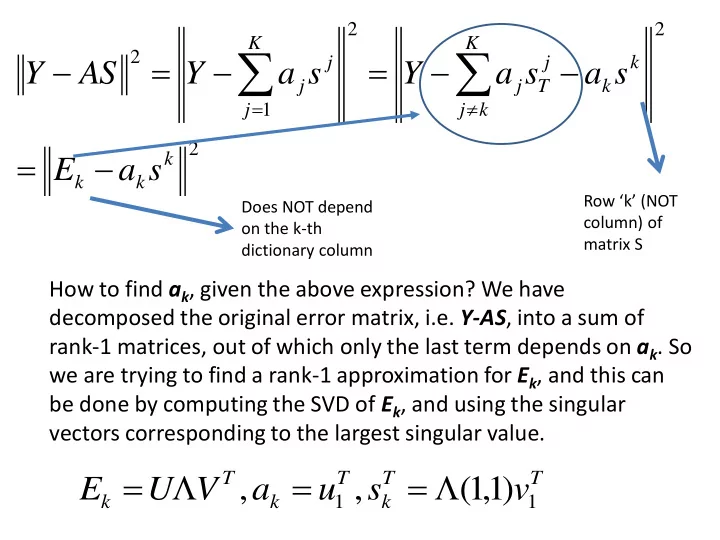

2 2 K K 2 j j k Y AS Y a s Y a s a s j j T k j 1 j k 2 k E a s k k Row ‘k’ (NOT Does NOT depend column) of on the k-th matrix S dictionary column How to find a k , given the above expression? We have decomposed the original error matrix, i.e. Y-AS , into a sum of rank-1 matrices, out of which only the last term depends on a k . So we are trying to find a rank-1 approximation for E k , and this can be done by computing the SVD of E k , and using the singular vectors corresponding to the largest singular value. T T T T E U V , a u , s ( 1 , 1 ) v k k 1 k 1
Problem! The dictionary codes may no more be sparse! SVD does not have any in-built sparsity constraint in it! So, we proceed as follows: Considers only those columns of Y (i.e. only k { i | s ( i ) 0 } those data-points) that k actually USE the k-th dictionary atom, effectively yielding a Consider the error matrix defined as follows: smaller matrix, of size p by | k | 2 2 k Y AS E ( a s ) k , k k k F k k T E U V This update affects the sparse k , k codes of only those data-points k T that used the k-th dictionary a U , s ( 1 , 1 ) V k 1 1 element, i.e. those that are part of k ω k .
http://www.cs.technion .ac.il/~elad/publications /journals/2004/32_KSV D_IEEE_TSP.pdf
Application: Image Compression • Recall JPEG algorithm • It divides the image to be compressed into non- overlapping patches of size 8 x 8. • It computes the 2D-DCT coefficients of each patch, quantizes them and stores only the non- zero coefficients – using Huffman encoding. • KSVD can be used in image compression by replacing the orthonormal 2D-DCT dictionary by an overcomplete dictionary trained on a database of similar images.
Application: Image Compression (Training Phase) • Training set for dictionary learning: a set of 11000 patches of size 8 x 8 – taken from a face image database. Dictionary size K = 441 atoms (elements). • OMP used in the sparse coding step during training – stopping criterion is a fixed number of coefficients T 0 = 10. • Over-complete Haar and DCT dictionaries – of size 64 x 441 – and ortho-normal DCT basis of size 64 x 64 (JPEG), also used for comparison.
http://www.cs.technion.ac.il/~elad/publication s/journals/2004/32_KSVD_IEEE_TSP.pdf
Application: Image Compression (Testing Phase) • A lossy image compression algorithm is evaluated using an ROC curve – the X axis contains the average number of bits (BPP) to store the signal. • The Y-axis is the compression error or PSNR. Normally, the acceptable error e is fixed and the number of bits is calculated. • The test image is divided into non-overlapping patches of size 8 x 8. • Each patch is projected onto the trained dictionary and its sparse code is obtained using OMP given a fixed error e .
http://www.cs.t echnion.ac.il/~el ad/publications/ journals/2004/3 2_KSVD_IEEE_TS P.pdf Even if the error ‘e’ for the OMP was fixed, we need to compute the total MSE between the true and the compressed image. This is due to effects of quantization while storing the sparse coefficient values for each patch.
Application: Image Compression (Testing Phase) • The encoded image contains the following: 1. Sparse-code coefficients for each patch and the indices of each non-zero coefficient (in the dictionary). 2. The number of coefficients used to represent each patch (different patches will need different number of coefficients).
Application: Image Compression (Testing Phase) • The average number of bits per pixel (BPP) is calculated as: Sum total of the number of coefficients a # patches # coeffs ( b Q ) representing BPP each patch # pixels Number of bits Number of bits Number of bits required to store the required to code required to store the dictionary index for each coefficient number of each coefficient (quantization level) coefficients for each patch Huffman encoding
http://www.cs.technion.ac.il/~elad/publication s/journals/2004/32_KSVD_IEEE_TSP.pdf
Application: Image Denoising • KSVD for denoising seeks to minimize the following objective function: 2 2 ( X , D , { }) arg min X Y D R X ij X , D , { } ij ij ij ij ij 0 i , j i , j Y = noisy image X = underlying clean image (to be estimated) ij = sparse dictionary coefficients for patch at location (i,j) D = dictionary R ij = matrix that extracts the patch x ij from image X, i.e. x ij = R ij X
Application: Image Denoising • Note: The dictionary may be learned a priori from a corpus of image patches. The patches from the noisy image can then be denoised by mere sparse coding. • The more preferable method is to train the dictionary directly on the noisy image in tandem with the sparse coding step (as in the previous slide). • This avoids having to depend on the training set and allows for tuning of the dictionary to the underlying image structure (as opposed to the structure of some other images).
KSVD Algorithm for Denoising (Dictionary learned on the noisy image) • Set X = Y, D = overcomplete DCT • Until some “convergence” criterion is satisfied, repeat the following: 1. Obtain the sparse codes for every patch (typically using OMP) as follows: 2 2 i , j , min s.t. R X D C ij ij ij 0 2. Perform the dictionary learning update typical for KSVD. • Estimate the final image X by averaging the reconstructed overlapping patches, OR estimate X given D and ij : 2 2 X arg min X Y D R X X ij ij ij T 1 T X ( I R R ) ( Y R D ) ij ij ij ij ij ij
KSVD Algorithm for Denoising (Dictionary learned on the noisy image) 2 2 X arg min X Y D R X X ij ij ij T 1 T X ( I R R ) ( Y R D ) ij ij ij ij ij ij 30 set to This equation is a mathematically rigorous way to show how X was reconstructed by averaging overlapping denoised patches together with the noisy image as well.
Baseline for comparison: method by Portilla et al, “Image denoising using scale mixture of Gaussians in the wavelet domain”, IEEE TIP 2003. http://www.cs.technion.ac.il/~elad/publication s/journals/2005/KSVD_Denoising_IEEE_TIP.pdf
http://www.cs.technion.ac.il/~elad/publication s/journals/2005/KSVD_Denoising_IEEE_TIP.pdf
http://www.cs.technion.ac.il/~elad/Variou s/KSVD_Matlab_ToolBox.zip
http://www.cs.technio n.ac.il/~elad/publicati ons/journals/2005/KS VD_Denoising_IEEE_TI P.pdf
Application of KSVD: Filling in Missing Pixels http://www.cs.technion.ac.il/~elad/publication s/journals/2004/32_KSVD_IEEE_TSP.pdf
Application of KSVD: Filling in Missing Pixels • An over-complete dictionary is trained a priori on a set of face images. • A test face image (not part of the training set) is synthetically degraded by masking out 50 to 70 percent of the pixels. • Patches from the degraded image are sparse coded by projection onto the trained dictionary using OMP. • OMP is modified so that only the non-degraded pixels are considered during any error computation (the dictionary elements are therefore appropriately re- scaled to unit norm).
Application of KSVD: Filling in Missing Pixels 2 y n 1 patch in corrupted image at location ( i , j ) ij ~ y |P| 1 vector containing the P non - corrupted ij intensitie s from y ij ~ 2 2 P n n K K 1 y Ds where R , D R , s R ij ij ij ij ij 2 ~ E ({ s }) y Ds s.t. s T ij ij ij ij ij 0 0 i , j D learned a - priori Sparse codes determined using OMP or ISTA
Application of KSVD: Filling in Missing Pixels • The patches are reconstructed in the following manner: y Ds ij ij NOTE: Dictionary elements without masking!!
Blind compressed sensing • In standard compressed sensing, we assume knowledge of the basis (may be orthonormal or even overcomplete) in which the signal is sparse. • However this knowledge may not be available to us always. • For example, consider a remote sensing application with compressive acquisitions of water bodies followed by forests over mountain ranges. • Images of the former are likely to be highly sparse in DCT whereas the latter may not be – and another basis may serve a better purpose. • Blind compressed sensing is the task of inferring the signal basis as well as the signal coefficients directly from the compressed data.
Blind compressed sensing • Consider N signals and their compressive measurements in the following form: m n n m y x , R , x R , y R , m n i i i i i i i • Our sparsity model for each signal is as follows: n K K x D , D R , R i i i • Combined model is: y D i i i i
Recommend
More recommend