2 8 G a const H 2 1 /a 4 = , = = . 3 a a 4 - PowerPoint PPT Presentation

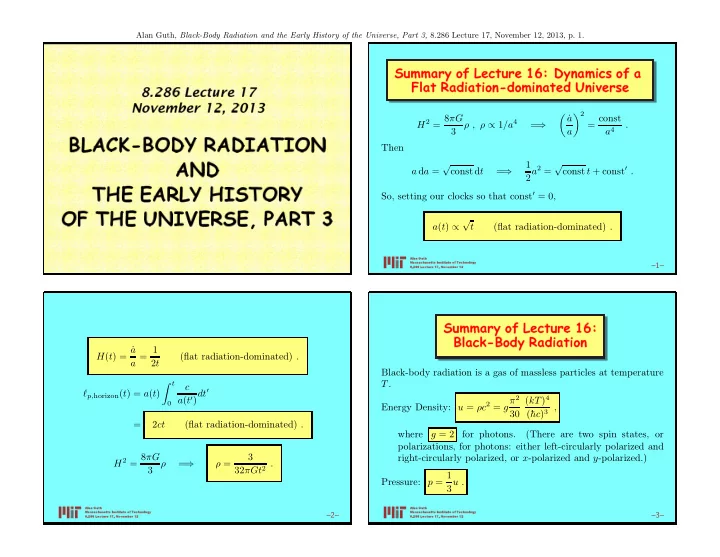
Alan Guth, Black-Body Radiation and the Early History of the Universe, Part 3, 8.286 Lecture 17, November 12, 2013, p. 1. Summary of Le ture 16: Dynami s of a Flat Radiation-dominated Universe 8.286 Le ture 17 November 12, 2013 � ˙ � 2 8 πG a const H 2 ∝ 1 /a 4 = ρ , ρ = = . ⇒ 3 a a 4 BLACK-BODY RADIATION Then √ 1 √ AND a 2 = const t + const ′ . a d a = const d t = ⇒ 2 THE EARLY HISTORY So, setting our clocks so that const ′ = 0, OF THE UNIVERSE, PART 3 √ a ( t ) t (flat radiation-dominated) . ∝ Alan Guth Massa husetts Institute of T e hnology –1– 8.286 Le ture 17, November 12 Summary of Le ture 16: Bla k-Body Radiation a ˙ 1 H ( t ) = = (flat radiation-dominated) . a 2 t Black-body radiation is a gas of massless particles at temperature T . t c � dt ′ ℓ p, horizon ( t ) = a ( t ) 2 ( ) 4 0 a ( t ′ ) π kT u = ρc 2 Energy Density: = g , 30 (¯ hc ) 3 = 2 ct (flat radiation-dominated) . where g = 2 for photons. (There are two spin states, or polarizations, for photons: either left-circularly polarized and 8 πG 3 right-circularly polarized, or x -polarized and y -polarized.) H 2 = ρ = ρ = . ⇒ 3 32 πGt 2 1 Pressure: p = u . 3 Alan Guth Alan Guth Massa husetts Institute of T e hnology Massa husetts Institute of T e hnology –2– –3– 8.286 Le ture 17, November 12 8.286 Le ture 17, November 12

Alan Guth, Black-Body Radiation and the Early History of the Universe, Part 3, 8.286 Lecture 17, November 12, 2013, p. 2. 2 π 2 k 4 T 3 ζ (3) ( kT ) 3 Number density: n = g ∗ , Entropy density: s = g . π 2 hc ) 3 (¯ hc ) 3 45 (¯ where ζ (3) is the Riemann zeta function with argument 3, Entropy is a measure of “disorder,” in the sense that it measures the number of microscopic quantum states that contribute to a given macroscopic state. The second law 1 1 1 ζ (3) = + + + · · · ≈ 1 . 202 , of thermodynamics says that entropy never decreases. If 1 3 2 3 3 3 the system stays close to thermal equilibrium, then entropy is essentially conserved. In the early universe, entropy is and g ∗ = 2 for photons. essentially conserved for all processes except for inflation. Alan Guth Alan Guth Massa husetts Institute of T e hnology Massa husetts Institute of T e hnology –4– –5– 8.286 Le ture 17, November 12 8.286 Le ture 17, November 12

MIT OpenCourseWare http://ocw.mit.edu 8.286 The Early Universe Fall 2013 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.