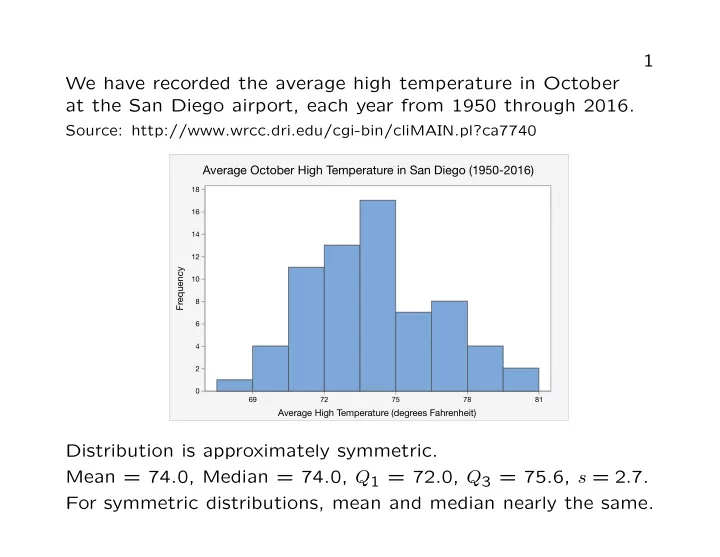
1 We have recorded the average high temperature in October at the - PowerPoint PPT Presentation

1 We have recorded the average high temperature in October at the San Diego airport, each year from 1950 through 2016. Source: http://www.wrcc.dri.edu/cgi-bin/cliMAIN.pl?ca7740 Average October High Temperature in San Diego (1950-2016) 18 16 14 12 Frequency 10 8 6 4 2 0 69 72 75 78 81 Average High Temperature (degrees Fahrenheit) Distribution is approximately symmetric. Mean = 74.0, Median = 74.0, Q 1 = 72.0, Q 3 = 75.6, s = 2 . 7. For symmetric distributions, mean and median nearly the same.

2 We have recorded the amount of precipitation in October at the San Diego airport, each year from 1950 through 2016. Source: http://www.wrcc.dri.edu/cgi-bin/cliMAIN.pl?ca7740 October Precipitation Totals in San Diego (1950-2016) 40 30 Frequency 20 10 0 0.00 0.75 1.50 2.25 3.00 3.75 4.50 Precipitation (inches) There is one outlier (4.98 inches of rain in October, 2004). Mean = 0.43, Median = 0.14, Q 1 = 0.01, Q 3 = 0.58, s = 0 . 75. For distributions skewed to the right, the mean tends to be larger than the median, and the upper quartile tends to be farther from the median than the lower quartile.

3 We have the Shannon Biodiversity Index for 632 soil samples collected from Scripps Coastal Reserve by BILD 4 students. Source: data provided to the instructor by Professor Stanley Lo Biodiversity in soil samples from Scripps Coastal Reserve 200 150 Frequency 100 50 0 2.00 2.20 2.40 2.60 2.80 3.00 3.20 3.40 Shannon Biodiversity Index Mean = 3.08, Median = 3.13, Q 1 = 2.96, Q 3 = 3.24. For distributions skewed to the left, the mean tends to be smaller than the median, and the upper quartile tends to be closer to the median than the lower quartile.

4 Data on eruptions of the Old Faithful geyser in Yellowstone. Source: http://rweb.stat.umn.edu/R/library/alr3/help/oldfaith Old Faithful Eruptions (October, 1980) 35 30 25 Frequency 20 15 10 5 0 90 120 150 180 210 240 270 300 Duration of Eruption (seconds) Distribution is bimodal. Mean = 209.9, Median = 240, Q 1 = 129.8, Q 3 = 268, s = 68 . 4. For bimodal distributions, summary statistics do not describe the distribution well. One should always plot the data.

Examples of Correlations 5 r = 0.01 r = 0.46 r = 0.76 r = 1

Examples of Correlations 6 r = -0.33 r = -0.69 r = -0.98 r = -1

7 r = -0.05 0.5 0.4 0.3 0.2 0.1 0.0 0.0 0.2 0.4 0.6 0.8 1.0 Here there is a strong association but no correlation. Correlation measures only linear association and should not be used to describe nonlinear relationships.

8 r = 0.44 1.1 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Here there is a weak correlation of 0.44. If the outlier is removed, there is a very strong correlation of 0.99. Outliers can have a large effect on correlation.

9 Data on SAT scores, GPAs of 1000 students Source: http://www.cvgs.k12.va.us/DIGSTATS/main/inferant/a gpas.html College GPA and SAT Scores 4 3 College GPA 2 1 0 500 600 700 800 900 1000 1100 1200 1300 1400 Combined SAT Score Correlation between combined SAT score, college GPA is 0.46. Correlation between high school GPA and college GPA is 0.54. High school GPA is a better predictor of college performance than SAT scores.

10 Data on student evaluations in 1184 UCSD Math courses (Fall 2010 – Spring 2017) Source: http://www.cape.ucsd.edu/responses/Results.aspx Learning and Study Time 5.0 4.5 Amount Learned (1-5 scale) 4.0 3.5 3.0 2.5 2.0 2 4 6 8 10 12 14 16 18 Hours of studying per week Correlation between “Hours” and “Learned”: 0.29 Correlation between “Hours” and “Recommend course”: -0.08 Correlation between “Hours” and “Recommend instructor”: 0.08

11 Data on 157 countries with population over 1 million. Source: https://www.cia.gov/library/publications/the-world-factbook/index.html Life Expectancy and Fertility Rate 80 70 Life Expectancy 60 50 40 30 1 2 3 4 5 6 7 8 Children per woman There is a moderately strong negative correlation of -0.77. High fertility rates do not cause shorter lifespans. Correlation does not imply causation. Economic conditions are a lurking variable.

12 Data on 599 women aged 45-74, Whickham, UK. Women surveyed 1972-1974, again 20 years later. Source: Appleton, D.R., French, J.M., and Vanderpump, M.V. Ignoring a covariate: An example of Simpson’s paradox. The American Statistician , 50 (1996), 340-341 . Smokers: 107 of 271 (39.5%) died. Non-smokers: 153 of 328 (46.6%) died. Age Smokers Non-Smokers 45-54 27 of 130 (20.8%) died 12 of 78 (15.4%) died 55-64 51 of 105 (48.6%) died 40 of 121 (33.1%) died 65-74 29 of 36 (80.6%) died 101 of 129 (78.3%) died Simpson’s paradox: A higher percentage of non-smokers died overall. A higher percentage of smokers died in each age group. The positive association between smoking and living 20 more years does not mean that smoking causes people to live longer. Age is a lurking variable.

13 Data on graduate admissions at U.C. Berkeley. Source: D. Freedman, R. Pisani, R. Purves. Statistics . 4th ed. Norton, New York . In the fall of 1973, U.C. Berkeley admitted 44% of 8442 men who applied for graduate school, and 35% of 4321 women. Department Men % Accepted Women % Accepted A 825 62 108 82 B 560 63 25 68 C 325 37 593 34 D 417 33 375 35 E 191 28 393 24 F 373 6 341 7 Most individual departments admitted a similar percentage of male and female applicants. However, male applicants applied more often to departments with a higher acceptance rate.

14 Data on GPA and SAT scores of 1000 college students. Source: http://www.cvgs.k12.va.us/DIGSTATS/main/inferant/a gpas.html Predicting College GPA from SAT Scores 4 3 College GPA 2 1 0 500 600 700 800 900 1000 1100 1200 1300 1400 Combined SAT Score Predictor Coefficient Constant .002 y = . 002 + . 00239 x ˆ SAT Score .00239 SAT = 1200, predicted GPA = .002 + (.00239)(1200) = 2.87.

15 Data on winning times in the Boston marathon, 1940-1990. Source: http://www.bostonmarathonmediaguide.com/champions/ Winning times in the Boston marathon (1940-1990) 155 150 Winning time (minutes) 145 140 135 130 1940 1950 1960 1970 1980 1990 Year y = 1072 . 77 − . 47519 x ˆ

16 Predicted Actual Error 1991 126.7 131.1 4.4 1992 126.2 128.3 2.1 2016 114.8 132.8 18.0 2017 114.3 129.6 15.3 Winning times in the Boston marathon (1940-2017) 155 150 145 Winning time (minutes) 140 135 130 125 120 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 Year Extrapolation (making predictions outside the range of the data) can be dangerous.

17 Outliers in Regression It is important to consider carefully the effect of outliers on the position of the regression line. We say a point has high leverage if it is extreme in the x -direction. We say a point is influential if removing it would greatly change the position of the regression line. A high leverage point is often (not always) influential because the regression line tends to be drawn towards high leverage points. Regression is usually not appropriate when there is an influential point.

18 High Leverage, Not Influential High Leverage, Influential 1.2 2.0 1.0 1.5 0.8 0.6 1.0 0.4 0.5 0.2 0.0 0.0 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 1.5 2.0 Low Leverage, Not Influential 1.6 1.4 1.2 1.0 0.8 0.6 0.4 0.2 0.0 0.0 0.2 0.4 0.6 0.8 1.0

19 Data on mortality rates of white males from melanoma in the 48 contiguous states, 1950-1959. Source: G. van Belle, L. Fisher, P. Heagerty, T. Lumley. (2004) Biostatistics . 2nd ed. Wiley. Mortality Rates from Melanoma (1950-1959) 225 Mortality rate per 10,000,000 200 175 150 125 100 30 35 40 45 50 Latitude R 2 = . 685 ˆ y = 388 . 31 − 5 . 9665 x , The value of R 2 means 68.5 percent of the variation in mortality rates from melanoma is explained by the latitude of the state.

20 Residual Plot 50 40 30 20 Residual 10 0 -10 -20 -30 -40 30 35 40 45 50 Latitude The residual plot looks like a random scatter. There are no apparent patterns. In particular, there is no indication of curva- ture and there are no outliers. Consequently, linear regression is appropriate.

21 Data on length and weight of 42 Rainbow trout Source: http://www.seattlecentral.org/qelp/sets/023/023.html Goal: to predict weight from length so that it is not necessary to weigh fish. Weights and lengths of rainbow trout 1400 1200 1000 Weight (grams) 800 600 400 200 0 250 300 350 400 450 500 Length (millimeters) R 2 = . 939 ˆ y = − 881 . 9 + 3 . 92 x ,

22 Residual Plot 250 200 150 Residual 100 50 0 -50 -100 250 300 350 400 450 500 Length (millimeters) The residual plot shows some curvature. This suggests that the relationship between the variables is not linear. Try taking the cube root of the weights.

23 Cube root of weight vs Length 11 10 Cube root of weight 9 8 7 6 5 250 300 350 400 450 500 Length (millimeters) y 1 / 3 = . 7383 + . 01994 x , R 2 = . 971 ˆ For a fish of length 400 millimeters, our prediction for the cube root of the weight is . 7383 + ( . 01994)(400) = 8 . 7143, so our prediction for the weight in grams is 8 . 7143 3 = 661 . 8. Caution: when making predictions, do not forget to convert back to the original units.