1 Dominance Frontiers Revisited Dominance Frontiers and SSA - PowerPoint PPT Presentation

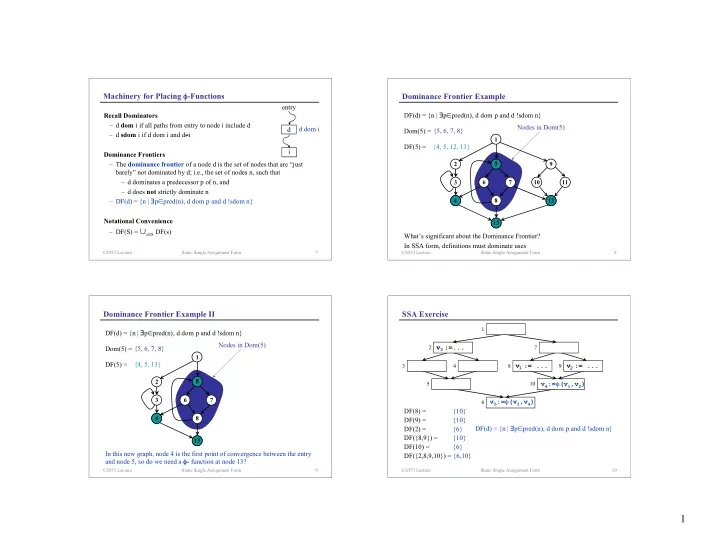
Machinery for Placing φ -Functions Dominance Frontier Example entry Recall Dominators DF(d) = {n | ∃ p ∈ pred(n), d dom p and d !sdom n} – d dom i if all paths from entry to node i include d Nodes in Dom(5) d dom i d {5, 6, 7, 8} Dom(5) = – d sdom i if d dom i and d ≠ i 1 DF(5) = {4, 5, 12, 13} i Dominance Frontiers – The dominance frontier of a node d is the set of nodes that are “just 2 5 5 9 barely” not dominated by d; i.e., the set of nodes n, such that – d dominates a predecessor p of n, and 3 6 7 10 11 – d does not strictly dominate n 4 8 12 – DF(d) = {n | ∃ p ∈ pred(n), d dom p and d !sdom n} Notational Convenience 13 – DF(S) = ∪ s ∈ S DF(s) What’s significant about the Dominance Frontier? In SSA form, definitions must dominate uses CS553 Lecture Static Single Assignment Form 7 CS553 Lecture Static Single Assignment Form 8 Dominance Frontier Example II SSA Exercise 1 DF(d) = {n | ∃ p ∈ pred(n), d dom p and d !sdom n} Nodes in Dom(5) 2 v :=... 7 Dom(5) = {5, 6, 7, 8} 3 1 DF(5) = {4, 5, 13} v := ... v := ... 3 4 8 9 1 2 5 5 2 5 10 v 4 := φ (v 1 ,v 2 ) 3 6 7 v 5 := φ (v 3 ,v 4 ) 6 DF(8) = {10} 4 8 DF(9) = {10} DF(2) = {6} DF(d) = {n | ∃ p ∈ pred(n), d dom p and d !sdom n} DF({8,9}) = {10} 13 DF(10) = {6} In this new graph, node 4 is the first point of convergence between the entry DF({2,8,9,10}) = {6,10} and node 5, so do we need a φ - function at node 13? CS553 Lecture Static Single Assignment Form 9 CS553 Lecture Static Single Assignment Form 10 1

Dominance Frontiers Revisited Dominance Frontiers and SSA Suppose that node 3 defines variable x Let – DF 1 (S) = DF(S) x ∈ Def(3) {5} DF(3) = 1 – DF i+1 (S) = DF(S ∪ DF i (S)) 2 3 4 Iterated Dominance Frontier – DF ∞ (S) 5 Theorem 6 – If S is the set of CFG nodes that define variable v, then DF ∞ (S) is the set Do we need to insert a φ - function for x anywhere else? of nodes that require φ -functions for v Yes. At node 6. Why? CS553 Lecture Static Single Assignment Form 11 CS553 Lecture Static Single Assignment Form 12 Algorithm for Inserting φ -Functions Variable Renaming for each variable v Basic idea WorkList ← ∅ – When we see a variable on the LHS, create a new name for it EverOnWorkList ← ∅ – When we see a variable on the RHS, use appropriate subscript AlreadyHasPhiFunc ← ∅ for each node n containing an assignment to v Easy for straightline code Put all defs of v on the worklist WorkList ← WorkList ∪ {n} x = x 0 = EverOnWorkList ← WorkList = x = x 0 while WorkList ≠ ∅ x = x 1 = Remove some node n from WorkList = x = x 1 for each d ∈ DF(n) if d ∉ AlreadyHasPhiFunc Use a stack when there’s control flow Insert at most one φ function per node Insert a φ -function for v at d – For each use of x, find the definition of x that dominates it AlreadyHasPhiFunc ← AlreadyHasPhiFunc ∪ {d} if d ∉ EverOnWorkList x = x 0 = Traverse the dominance tree WorkList ← WorkList ∪ {d} Process each node at most once EverOnWorkList ← EverOnWorkList ∪ {d} = x = x 0 CS553 Lecture Static Single Assignment Form 13 CS553 Lecture Static Single Assignment Form 14 2

Dominance Tree Example Variable Renaming (cont) The dominance tree shows the dominance relation Data Structures – Stacks[v] ∀ v Holds the subscript of most recent definition of variable v, initially empty 1 – Counters[v] ∀ v 1 Holds the current number of assignments to variable v; initially 0 5 2 5 9 2 4 5 13 9 12 pop Auxiliary Routine push 1 3 6 7 10 11 procedure GenName(variable v) 3 6 8 7 10 11 i := Counters[v] 2 4 5 13 9 12 4 8 12 Dominance Tree push i onto Stacks[v] Counters[v] := i + 1 3 6 8 7 10 11 13 Use the Dominance Tree to remember the most CFG recent definition of each variable CS553 Lecture Static Single Assignment Form 15 CS553 Lecture Static Single Assignment Form 16 Variable Renaming Algorithm Transformation from SSA Form procedure Rename(block b) Proposal if b previously visited return Call Rename(entry-node) – Restore original variable names ( i.e ., drop subscripts) for each φ -function p in b – Delete all φ -functions GenName(LHS(p)) and replace v with v i , where i=Top(Stack[v]) for each statement s in b (in order) for each variable v ∈ RHS(s) Complications replace v by v i , where i = Top(Stacks[v]) x 0 = − What if versions get out of order? for each variable v ∈ LHS(s) x 1 = (simultaneously live ranges) GenName(v) and replace v with v i , where i=Top(Stack[v]) = x 0 for each s ∈ succ(b) (in CFG) = x 1 j ← position in s’s φ -function corresponding to block b Alternative for each φ -function p in s Φ ( , , ) − Perform dead code elimination (to prune φ -functions) replace the j th operand of RHS(p) by v i , where i = Top(Stack[v]) for each s ∈ child(b) (in DT) Recurse using Depth First Search − Replace φ -functions with copies in predecessors Rename(s) − Rely on register allocation coalescing to remove unnecessary copies for each φ -function or statement t in b Unwind stack when done with this node for each v i ∈ LHS(t) Pop(Stack[v]) CS553 Lecture Static Single Assignment Form 17 CS553 Lecture Static Single Assignment Form 18 3

Backward Analyses vs. Forward Analyses Static Single Information Form (SSI) For forward data-flow analysis, at phi node apply meet function For backward data-flow analysis? 1 2 v 0 :=... 3 v 1 :=... v 2 := φ (v 0 ,v 1 ) 4 ...v 2 ... Ananian’s Masters Thesis, 1997 MIT CS553 Lecture Static Single Assignment Form 19 CS553 Lecture Static Single Assignment Form 20 Concepts Next Time SSA construction Assignments – Place phi nodes – HW1 due – Variable renaming Lecture Transformation from SSA to executable code depends on the – Using SSA for program optimization optimizations dead-code elimination and copy propagation Backward data-flow analyses can use SSI modification to SSA CS553 Lecture Static Single Assignment Form 21 CS553 Lecture Static Single Assignment Form 22 4