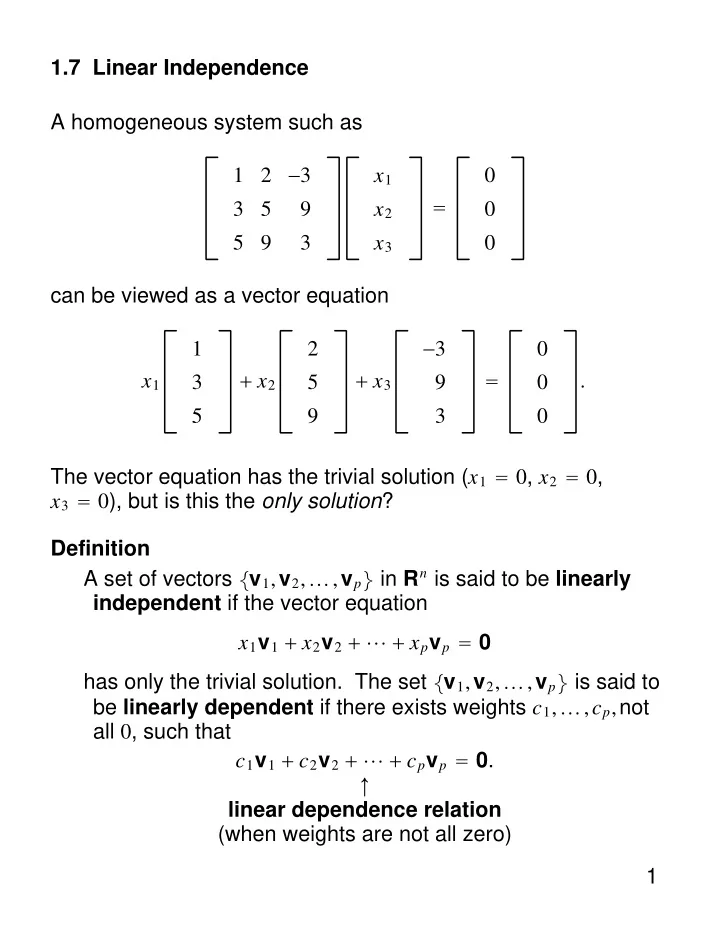
1.7 Linear Independence A homogeneous system such as 1 2 3 x 1 0 - PDF document

1.7 Linear Independence A homogeneous system such as 1 2 − 3 x 1 0 3 5 9 x 2 0 = 5 9 3 x 3 0 can be viewed as a vector equation 1 2 − 3 0 x 1 + x 2 + x 3 . 3 5 9 0 = 5 9 3 0 The vector equation has the trivial solution ( x 1 = 0 , x 2 = 0 , x 3 = 0 ), but is this the only solution ? Definition A set of vectors  v 1 , v 2 , … , v p  in R n is said to be linearly independent if the vector equation x 1 v 1 + x 2 v 2 + ⋯ + x p v p = 0 has only the trivial solution. The set  v 1 , v 2 , … , v p  is said to be linearly dependent if there exists weights c 1 , … , c p , not all 0 , such that c 1 v 1 + c 2 v 2 + ⋯ + c p v p = 0 . ↑ linear dependence relation (when weights are not all zero) 1

1 2 − 3 EXAMPLE Let v 1 = , v 2 = , v 3 = . 3 5 9 5 9 3 a. Determine if  v 1 , v 2 , v 3  is linearly independent. b. If possible, find a linear dependence relation among v 1 , v 2 , v 3 . Solution: (a) 1 2 − 3 0 . x 1 + x 2 + x 3 3 5 9 0 = 5 9 3 0 Augmented matrix: 1 2 − 3 0 1 2 − 3 0 1 2 − 3 0 3 5 9 0 0 − 1 18 0 0 − 1 18 0 ∼ ∼ 5 9 3 0 0 − 1 18 0 0 0 0 0 x 3 is a free variable ⇒ there are nontrivial solutions.  v 1 , v 2 , v 3  is a linearly dependent set 2

1 0 33 0 x 1 = (b) Reduced echelon form: 0 1 − 18 0 x 2  = 0 0 0 0 x 3 Let x 3 = _____ (any nonzero number). Then x 1 = _____ and x 2 = _____ . 1 2 − 3 0 ____ + ____ + ____ 3 5 9 0 = 5 9 3 0 or ____ v 1 + ____ v 2 + ____ v 3 = 0 (one possible linear dependence relation) 3

Linear Independence of Matrix Columns A linear dependence relation such as 1 2 − 3 0 − 33 + 18 + 1 3 5 9 0 = 5 9 3 0 can be written as the matrix equation: 1 2 − 3 − 33 0 . 3 5 9 18 0 = 5 9 3 1 0 Each linear dependence relation among the columns of A corresponds to a nontrivial solution to A x = 0 . The columns of matrix A are linearly independent if and only if the equation A x = 0 has only the trivial solution. 4

Special Cases Sometimes we can determine linear independence of a set with minimal effort. 1 . A Set of One Vector Consider the set containing one nonzero vector:  v 1  The only solution to x 1 v 1 = 0 is x 1 = _____. So  v 1  is linearly independent when v 1 ≠ 0 . 5

2 . A Set of Two Vectors EXAMPLE Let 2 4 2 2 u 1 = , u 2 = , v 1 = , v 2 = . 1 2 1 3 a. Determine if  u 1 , u 2  is a linearly dependent set or a linearly independent set. b. Determine if  v 1 , v 2  is a linearly dependent set or a linearly independent set. Solution: (a) Notice that u 2 = _____ u 1 . Therefore _____ u 1 + _____ u 2 = 0 This means that  u 1 , u 2  is a linearly ________________ set. 6

(b) Suppose c v 1 + d v 2 = 0 . Then v 1 = v 2 if c ≠ 0 . But this is impossible since v 1 is ______ a multiple of v 2 which means c = _____ . Similarly, v 2 = v 1 if d ≠ 0 . But this is impossible since v 2 is not a multiple of v 1 and so d = 0 . This means that  v 1 , v 2  is a linearly _________________ set. A set of two vectors is linearly dependent if at least one vector is a multiple of the other. A set of two vectors is linearly independent if and only if neither of the vectors is a multiple of the other. 7

x 2 4 3 2 1 x 1 1 2 3 4 linearly ___________________ 3 2 1 1 2 3 linearly ___________________ 8

3 . A Set Containing the 0 Vector Theorem 9 A set of vectors S =  v 1 , v 2 , … , v p  in R n containing the zero vector is linearly dependent. Proof: Renumber the vectors so that v 1 = ____. Then ____ v 1 + _____ v 2 + ⋯ + _____ v p = 0 which shows that S is linearly ________________. 4 . A Set Containing Too Many Vectors Theorem 8 If a set contains more vectors than there are entries in each vector, then the set is linearly dependent. I.e. any set  v 1 , v 2 , … , v p  in R n is linearly dependent if p > n . Outline of Proof: is n × p A = v 1 v 2 ⋯ v p Suppose p > n .  A x = 0 has more variables than equations  A x = 0 has nontrivial solutions  columns of A are linearly dependent 9

EXAMPLE With the least amount of work possible, decide which of the following sets of vectors are linearly independent and give a reason for each answer. 3 9 a. , 2 6 1 4 1 2 3 4 5 6 7 8 9 0 b. Columns of 9 8 7 6 5 4 3 2 1 8 10

3 9 0 c. , , 2 6 0 1 3 0 8 2 d. 1 4 11

Characterization of Linearly Dependent Sets Consider the set of vectors  v 1 , v 2 , v 3 , v 4  in R 3 in EXAMPLE the following diagram. Is the set linearly dependent? Explain v 3 x 3 v 2 x 2 x 1 v 1 v 4 12

Theorem 7 An indexed set S =  v 1 , v 2 , … , v p  of two or more vectors is linearly dependent if and only if at least one of the vectors in S is a linear combination of the others. In fact, if S is linearly dependent, and v 1 ≠ 0 , then some vector v j ( j ≥ 2 ) is a linear combination of the preceding vectors v 1 , … , v j − 1 . 13