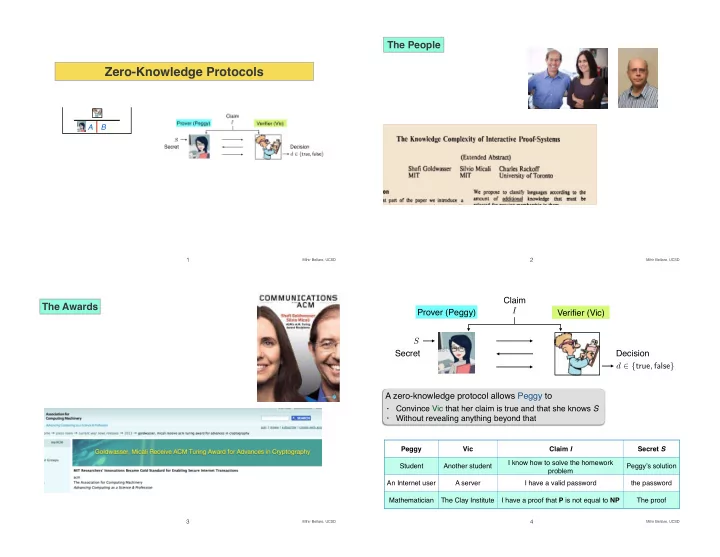

The People Zero-Knowledge Protocols A B 1 Mihir Bellare, UCSD 2 Mihir Bellare, UCSD Claim The Awards I Prover (Peggy) Verifier (Vic) S Secret Decision d ∈ { true , false } A zero-knowledge protocol allows Peggy to Convince Vic that her claim is true and that she knows S • Without revealing anything beyond that • Peggy Vic Claim I Secret S I know how to solve the homework Student Another student Peggy’s solution problem An Internet user A server I have a valid password the password Mathematician The Clay Institute I have a proof that P is not equal to NP The proof 3 Mihir Bellare, UCSD 4 Mihir Bellare, UCSD
Claim Ali-Baba’s Zero-Knowledge Protocol I Prover (Peggy) Verifier (Vic) S Secret Decision d ∈ { true , false } A zero-knowledge protocol allows Peggy to Convince Vic that her claim is true • Without revealing anything beyond that • Peggy Vic Claim I Secret S This story is used to explain zero-knowledge in many places. I know how to solve the homework Student Another student Peggy’s solution problem Including Wikipedia. But it doesn’t make a lot of sense. An Internet user A server I have a valid password the password We will use Joseph Jaeger’s variant. Mathematician The Clay Institute I have a proof that P is not equal to NP The proof 5 Mihir Bellare, UCSD 6 Mihir Bellare, UCSD MW[ A, B ] = Magic Words opening the A → B portal Ali Baba’s Ali Baba’s MW[ B, A ] = Magic Words opening the B → A portal ZK Protocol ZK Protocol Peggy has secret S ∈ { MW[ A, B ] , MW[ B, A ] } Peggy does not want Vic to know which of the two magic words she has. If Peggy knows MW[ A , B ] : If Peggy knows MW[ B , A ] : Peggy goes to A Peggy goes to B Completeness: If Peggy’s claim is true, meaning she knows either MW[ A , B ] or E E MW[ B , A ], and both parties follow the protocol, then Vic will accept. Final step, in either case: A B A B Why? Peggy can appear at whatever side Vic requests. Vic goes to E Vic goes to E C ← $ { A, B } A B C ← $ { A, B } “Peggy, please appear at C ” “Peggy, please appear at C ” If C = A A B A B A B If C = B 7 Mihir Bellare, UCSD 8 Mihir Bellare, UCSD
Ali Baba’s Ali Baba’s ZK Protocol ZK Protocol Completeness: If Peggy’s claim is true, meaning she knows either MW[ A , B ] or Completeness: If Peggy’s claim is true, meaning she knows either MW[ A , B ] or MW[ B , A ], and both parties follow the protocol, then Vic will accept. MW[ B , A ], and both parties follow the protocol, then Vic will accept. Soundness : If Peggy’s claim is false, meaning she knows neither MW[ A , B ] nor Soundness : If Peggy’s claim is false, meaning she knows neither MW[ A , B ] nor MW[ B , A ], then Vic will reject with probability at least 1/2, even if Peggy cheats, MW[ B , A ], then Vic will reject with probability at least 1/2, even if Peggy cheats, meaning does not follow the prescribed protocol. meaning does not follow the prescribed protocol. Why? Cheating Peggy can start at any X 2 { A, B } of her choice, but Vic picks C Zero-knowledge : If Peggy’s claim is true, and Peggy follows the protocol, then at random and cheating Peggy cannot appear at C 6 = X . Vic will not learn which of the two secrets MW[ A , B ], MW[ B , A ] Peggy knows. Why? Regardless of the secret, Vic sees Peggy appearing at whatever side he requests. 9 Mihir Bellare, UCSD 10 Mihir Bellare, UCSD Ali Baba’s Ali Baba’s ZK Protocol ZK Protocol Pegg’s claim is Peggy is Vic will Completeness TRUE honest always accept Soundness FALSE cheating accept with probability at most 1/2 Pegg’s claim is Peggy is Vic will Zero-knowledge TRUE honest not learn which of the two secrets Peggy knows Completeness TRUE honest always accept Soundness FALSE cheating accept with probability at most 1/2 This story may not make complete sense. To make zero-knowledge sensible, we need DEFINITIONS. Zero-knowledge TRUE honest not learn which of the two secrets Peggy knows The definitions are intriguing: how can one mathematically capture the ``knowledge’’ learned by interacting with another party? 11 Mihir Bellare, UCSD 12 12 Mihir Bellare, UCSD
Some math definitions Zero-knowledge protocol for Quadratic Residuosity Let N ≥ 1 be an integer. We say that x ∈ Z ∗ N is a square-root of X ∈ Z ∗ N modulo N if x 2 mod N = X . We say that X ∈ Z ∗ N is a square, or quadratic residue, modulo N , if it has a square root modulo N . N : X = x 2 mod N } SR ( N, X ) = { x 2 Z ∗ The set of square roots of X modulo N QR ( N ) = { X 2 Z ∗ N : SR ( N, X ) 6 = ; } The set of quadratic residues modulo N QR = { ( N, X ) : N � 1 and X 2 QR ( N ) } . The language of quadratic residues Example: Let N = 11. SR (11 , 5) = { 4 , 7 } x 1 2 3 4 5 6 7 8 9 10 SR (11 , 6) = ∅ x 2 mod 11 1 4 9 5 3 3 5 9 4 1 QR (11) = { 1 , 3 , 4 , 5 , 9 } N . Then X ∈ QR ( N ) if and only if X − 1 mod N ∈ QR ( N ). Fact: Let X ∈ Z ∗ N . Then x ∈ SR ( N, X ) if and only if x − 1 mod N ∈ SR ( N, X − 1 mod N ). Fact: Let x, X ∈ Z ∗ 13 Mihir Bellare, UCSD 14 Mihir Bellare, UCSD Complexity of QR Proving quadratic residuosity ( N , X ) Both parties have ( N , X ), the common input N : X = x 2 mod N } SR ( N, X ) = { x 2 Z ∗ The set of square roots of X modulo N x Peggy claims that ( N , X ) is in QR. QR ( N ) = { X 2 Z ∗ N : SR ( N, X ) 6 = ; } The set of quadratic residues modulo N Peggy has x such that x 2 mod N = X Prover Peggy Verifier Vic QR = { ( N, X ) : N � 1 and X 2 QR ( N ) } . The language of quadratic residues Definition: Vic accepts if d = true Input: (N,X) Input: N Return d ∈ { true , false } Question: Is (N,X) in QR? Find: Some X in QR( N ) The protocol is the prescribed, shown steps for the parties. A party can follow the protocol Input: (N,X) in QR This is easy : Pick x ← $ Z ∗ (it is honest) or not (it is cheating). Vic is always honest , but not so Peggy. N Find: A square root x of X modulo N and return X ← x 2 mod N . These problems are hard : There are no (known) ( N,X ) is Peggy is Vic will efficient (polynomial-time) algorithms for them. Completeness in QR honest always accept But easy in some cases: There are polynomial-time algorithms when N is prime. Soundness not in QR cheating accept with probability at most 1/2 Zero-knowledge in QR honest not learn x 15 Mihir Bellare, UCSD 16 Mihir Bellare, UCSD
( N , X ) ( N , X ) A non-ZK protocol A non-ZK protocol x x Prover Peggy Verifier Vic Peggy has x such that x 2 mod N = X Prover Peggy Verifier Vic Cmt Cmt Cmt ← x Cmt ← x d ← (Cmt 2 mod N = X ) d ← (Cmt 2 mod N = X ) ; Return d ; Return d ( N , X ) Soundness: Peggy is cheating ? But X 62 QR ( N ) means there does not exist Cmt such that Cmt 2 mod N = X , so Vic will Prover Peggy Verifier Vic return d = false . Cmt Cmt ← ? d ← (Cmt 2 mod N = X ) ; Return d (N,X) is Peggy is Vic will (N,X) is Peggy is Vic will Completeness in QR honest always accept Completeness in QR honest always accept Soundness not in QR cheating never accept 17 Mihir Bellare, UCSD 18 Mihir Bellare, UCSD ( N , X ) A non-ZK protocol Splitting x Prover Peggy Verifier Vic Peggy has x such that x 2 mod N = X Suppose we split up X as: X = Cmt · Y mod N for some Cmt , Y ∈ Z ∗ N Cmt Then we have: Cmt ← x d ← (Cmt 2 mod N = X ) ; Return d — If (Cmt 2 QR ( N ) and Y 2 QR ( N )) then X 2 QR ( N ) Fact: — If X 62 QR ( N ) then (Cmt 62 QR ( N ) or Y 62 QR ( N )) √ √ √ Cmt · Y = Cmt · Y Proof Intuition: √ = X We are given that Cmt ∈ QR ( N ), so Cmt = c 2 mod N for some c ∈ Z ∗ N We are given that Y ∈ QR ( N ), so Y = y 2 mod N for some y ∈ Z ∗ N Let w = cy mod N Proof, Then w 2 mod N = c 2 y 2 mod N = Cmt · Y mod N (N,X) is Peggy is Vic will formally: But we are given that Cmt · Y mod N = X Completeness in QR honest always accept So w 2 mod N = X Soundness not in QR cheating never accept So X ∈ QR ( N ) Zero-knowledge in QR honest learn x , so ZK fails 19 Mihir Bellare, UCSD 20 Mihir Bellare, UCSD
Recommend
More recommend