x
play

x 0 E x P sin = E x E = x Q, y L 2 Cylindrically - PowerPoint PPT Presentation

Feb 26, 2024 •284 likes •351 views

Lecture 8 Uniformly charged rod, Q, L, with charge density Q y = = Q L Find E at P: Q = y L 2 E E y x 0 E x P sin = E x E = x

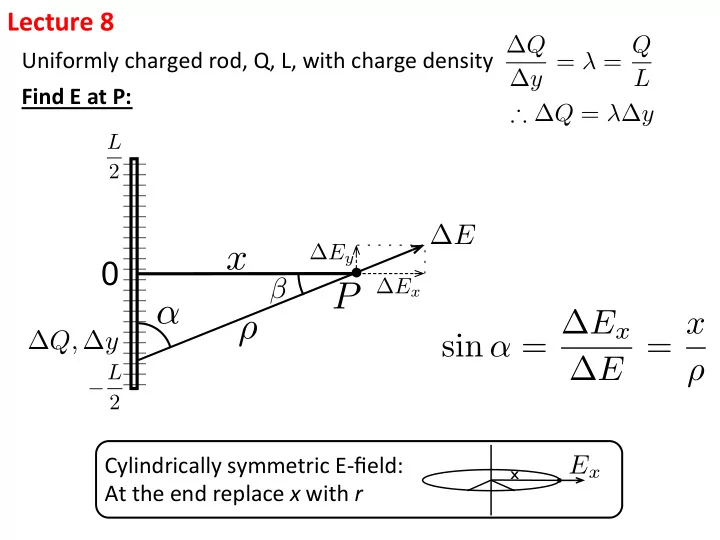
  1. Lecture ¡8 ¡ Uniformly ¡charged ¡rod, ¡Q, ¡L, ¡with ¡charge ¡density ¡ ∆ Q ∆ y = λ = Q L Find ¡E ¡at ¡P: ¡ ∴ ∆ Q = λ ∆ y L 2 ∆ E ∆ E y x 0 β ∆ E x P α sin α = ∆ E x ∆ E = x ρ ∆ Q, ∆ y − L ρ 2 Cylindrically ¡symmetric ¡E-­‑field: ¡ E x x At ¡the ¡end ¡replace ¡ x ¡with ¡ r ¡ ¡ ¡

  2. Uniformly ¡charged ¡rod ¡con1nued... ¡ ∆ E = k ( λ ∆ y ) , ∆ E x = ∆ E sin α ρ 2 Z dy E y = Σ k ( λ ∆ y ) sin α − ρ 2 sin α → k λ ρ 2 α 2 Change variable ∆ y → ∆ α P 0 dy ρ 2 = d α I.D. ¡ α + ∆ α x ∆ α α α 1 Z α 2 α 2 � d α x sin α = k λ = k λ � E x = k λ x ( − cos α ) x (cos α 1 − cos α 2 ) � � α 1 α 1

  3. Uniformly ¡charged ¡rod ¡con1nued... ¡ π − α 1 symmetry α 2 = π − α 1 cos α 1 − cos α 2 = 2 cos α 1 = 2 L/ 2 = L α 1 ρ 1 ρ 1 P 0 α r s ✓ L ◆ x 2 + r 1 = α 1 2 ∴ E x = k λ · L (see ¡pg ¡634) ¡ x 1 ρ 1 = kQ x 1 ρ 1

  4. Derive ¡Math ¡ID: ¡ y Change ¡of ¡Variable ¡in ¡IntegraAon: ¡ dy ρ 2 = d α x P Math ¡ID: ¡ 0 x α x tan α = ( − y ) ⌘ 2 = ρ 2 d α LHS = d d 1 1 d α tan α = cos 2 α = y 2 ⇣ y ρ ◆ dy ✓ 1 − 1 d α RHS = d d ( − y ) = ( − x ) d x d α = x dy y = ( − x ) y 2 y 2 d α d α d α d α LHS = d d d α RHS ∴ dy ρ 2 = d α ρ 2 y 2 = x dy x y 2 d α

  5. Back ¡to ¡Electric ¡Field ¡at ¡P: ¡ kQ E r = q � L � 2 r 2 + r 2 E r = kQ Farfield : r � L ( as expected ) r 2 2 kQ Nearfield : r ⌧ L E r = � L � r 2 2 Later ¡we ¡will ¡see ¡for ¡Gauss ¡Law ¡ one ¡finds ¡the ¡near ¡field ¡is ¡given ¡ by: ¡ � Check: ¡ 2 ⇡✏ 0 r · Q 1 RHS = rL 4 ⇡✏ 0 2 1 · � = r 2 ⇡✏ 0

  6. Ch. ¡16 ¡Hw1.003 ¡ F rod drop = ( − q ) E rod + qE rod < 0 + − E r = 2 k λ r � � � = q 2 k � 1 1 � F rod � � � � 1 − ✏ + � − � � drop r 1 + ✏ � − (1 + ✏ ) + (1 − ✏ ) = − 2 ✏ = − 2 s/ 2 r = − s � 2 kq λ · s r ∝ 1 r � F rod � � drop r 2 r

Recommend

More recommend