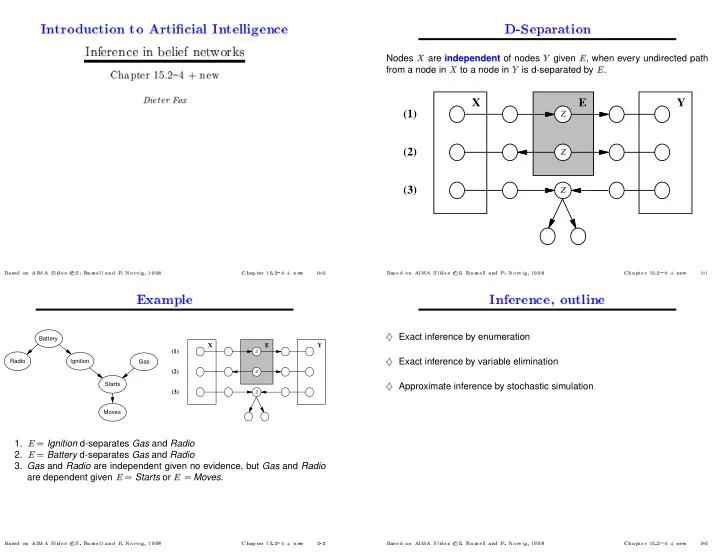
�✁ ❅❆ ❉ ❄ ❈ ❇ ✼ ✽ ✾ ❄ ❋ ❁ ❂❃ ❀❁ ✿ ✻✼✽✾ ✺ ❣ ❝ ❊ ✼ ❝ ■ P ◆❖ ◆ ▼ ▲ ❑ ❆ ❏ ✿ ✼ ❉❍ ● ✾ ❀ ✻ ❅ ❅ ✽ ❣ ❣ ✻ ❑ ❘ ✻ ◗ P ◆❖ ◆ ▼ ✂ ❆ ✽ ❏ ■ ✿ ❉❍ ● ✾ ❀ ✻ ❙ ■ ❝ ▼ ❣ ❝ ✌ ☞ ❵ ❢ ☛ ❞❡ ❬ ▼ ▼ ✽❨ ❀ ❳ ❲ ❱ ❉❯ ❚ ◗ ❘ ❅ ✻ ❆ ❏ ■ ✿ ❉❍ ● ✾ ❀ ❅ ▲ ❅ ✽ ✼ ✼ ❋ ❊ ❉ ❄ ❑ ▼ ❇ ❚ ❬ ❦ ✽❨ ❀ ❳ ❲ ❱ ❉❯ ▼ ◆ ■ ✽ ❙ ❘ ✻ ◗ P ◆❖ ❈ ✼ ❙ ✽❨ ✁ ✌ ✄ ✌ �✁❤ ❯ ❬ ❯ ❀ ✌ ❳ ❲ ❱ ❉❯ ❚ ▼ ■ ✽ ✞ ✐ ✽ ✺ ✾ ❅❆ ❄ ❁ ❂❃ ❀❁ ✿ ✻✼✽✾ ❥ ☎ ❥ ❥ ✌ ✁ ✟ ☞ ✂ ✝ ❅ ▲ ✽ ✱ ❀❁ ✿ ✻✼✽✾ ✺ ✸✹ ✷ ✴✶ ✳✴✵ ✲ ✧ ❁ ✰ ✯ ✮ ✭ ✫✬ ✪ ★✩ ✦✧ ✥ ❂❃ ❄ ✣ ✽ ■ ✿ ❉❍ ● ✾ ❀ ✻ ❅ ❅ ✼ ❅❆ ✼ ❋ ❊ ❉ ❄ ❈ ❇ ✼ ✽ ✾ ✤ ✢ ✼ ✂ ☞ ☞ ✂✌ �✁ ☞ ☛ ✟ ✞ ✟✡ ✄ ✍ ✠ ☎ ✂ ✁ ☎ ✟ ✂ ✝✞ ☎✆ ✄ ✟ ✌ ✜ ✖ ✓✛ ✚ ✒✘✙ ✏ ✑ ✒ ✕ ✗ ✒ ✏ ✁ ✕ ✒ ✔ ✏ ✒ ✓ ✒ ✎✏✑ ✌ ✞ ❏ ❆ ❑ ❀❁ ☎ ✁ ❛ ▲ ❜ ❝ ❛ ❜ ❝ ✺ ✻✼✽✾ ✿ ❂❃ ✂ ❁ ❄ ❅❆ ✾ ✽ ✼ ❇ ❈ ❄ ❉ ❊ ❋ ✼ ✟ ❦ ❲ ✽ ❱ ❉❯ ❚ ☛ ❩ ❬ ❩ ✌ ▼ ✽❨ ■ ❙ ❀ P ✄ ▼ ◆ ◆❖ ☛ ◗ ✻ ❵ ❳ ❘ ❴ ❭❫❪ are independent of nodes Nodes given , when every undirected path from a node in to a node in is d-separated by . X E Y (1) Z (2) Z (3) Z Exact inference by enumeration Battery X E Y (1) Z Exact inference by variable elimination Radio Ignition Gas (2) Z Starts Approximate inference by stochastic simulation (3) Z Moves Ignition d-separates Gas and Radio 1. Battery d-separates Gas and Radio 2. 3. Gas and Radio are independent given no evidence, but Gas and Radio Starts or Moves . are dependent given
♦❫♣ ♦❫♣ ♦❫♣ � ✈ ♥ ② ❮ ❰Ï Ð Ñ ⑥ ⑦ ④ ♦ ② ❣ ❮ ❰ Ï Ð Ò ⑥ ⑧ ♥ ♦ ⑨ q ♣ ✇ ✈ ⑤ st✉✈ ② ❣ ④ ♦ r ❣ st✉ ✈ q ⑨ ② ④ ♦ ① st✉✈ ❮ q ⑨ ② ✈ ♥ q r ❣ st✉✈ ✇ ① ❣ ② Ï ❰ ♣ ⑥ ⑦ ④ ♦ ✈ ② ⑥ ⑧ ♥ ♦ ⑨ q ✇ ♥ ✈ ② ④ ♦ r ❣ st✉✈ q ⑨ ② Ö Õ ♦ ② ⑤ ☎ Ð Ð Ó ④ ♦ r ❣ st✉✈ q ⑨ ② ❮ ❰ Ï Ô ❣ ④ ♦ ① ❣ st✉ ✈ q ⑨ ② ❮ ❰Ï Ð Õ ✁ ✂ ✟ ✃ ➨ ➬ ➀ ➇ ➃ ➯➲➳➵ ➊ ➱ ➊ ➱ ➊ ➴ ➶ ➆ ✺ ✻✼✽✾ ✿ ❀❁ ❂❃ ❁ ❄ ❅❆ ✾ ✽ ✼ ❇ ❈ ➨ ➀ ❉ ✁❤ ➃ ➯➲ ➳ ➵ ➊ ➊ ➼ ➑ ➊ ➍ ➊➎➏ ➍ ➮ ➂➃ ➱ ➪ → ➶ ➹ ➪ ➘ ➜ ❼❽ ❾ ❿ ➀ ➁ ❄ ❊ ② ❧ ❀ ✽❨ ❚ ❬ ❚ �✁❤ ✌ ✄ ✌ ✁ ✞ ✌ ☛ ❲ ✄ ✟ ☛ ❧ ☞ ✌ ✌ ☞ ✟ ❢ ✟ ✁ ☛ ❳ ❱ ❋ ❆ ✼ ✼ ✽ ❅ ❅ ✻ ❀ ✾ ● ❉❍ ✿ ■ ❏ ❑ ❉❯ ▲ ▼ ◆ ◆❖ P ◗ ✻ ❘ ❙ ✽ ■ ▼ ❚ ⑨ ⑤ ❣ ✌ ❲ ❳ ❀ ✽❨ Ý ❬ Ý Þ ☎ ❢ ❵ ☞ ❡ ❉❯ ✟ ✂ ♠ ☎ ❤ ✌ ❡ ☛ ✞ ✂ ✟ ✁❤ ✌ ❱ ❚ ✌ ■ ❋ ✼ ✼ ✽ ❅ ❅ ✻ ❀ ✾ ● ❉❍ ✿ ❏ ▼ ❆ ❑ ▲ ▼ ◆ ◆❖ P ◗ ✻ ❘ ❙ ✽ ■ ✄ ✁ ❉ ✻ ❉❍ ✿ ■ ❏ ❆ ❑ ▲ ▼ ◆ ◆❖ P ◗ ❘ ✾ ❙ ✽ ■ ▼ ❚ ❉❯ ❱ ❲ ❳ ❀ ✽❨ á ❬ ● ❀ ✞ ❅❆ ✌ ❶ ❷ ② à à ✺ ✻✼✽✾ ✿ ❀❁ ❂❃ ❁ ❄ ✾ ✻ ✽ ✼ ❇ ❈ ❄ ❉ ❊ ❋ ✼ ✼ ✽ ❅ ❅ ❊ ❄ ➀ ⑨ ② ⑥ ⑦ ④ ♦ ✈ ② ⑥ ⑧ Ö Ó ♦ ✇ ⑤ × ✇ ✈ ② Ö Ô ♦ ⑨ ② Ö Õ ♦ ⑨ ♥ ❣ ❣ ⑨ ♥ ② ⑥ ⑦ ④ ♦ ✈ ② ⑥ ⑧ ♥ ♦ q ② ♣ ✇ ✈ ② Ö Ô ♦ ⑨ ② Ö Õ ♦ ⑨ ② ⑤ ❈ ♦ ⑤ Ö Ñ ♦ × Ö Ø Ò Ø Ó Ô Õ × ❝ ② ✺ ✻✼✽✾ ✿ ❀❁ ❂❃ ❁ ❄ ❅❆ ✾ ✽ ✼ ❇ ❣ ② ♥ ✈ ② ⑥ ⑦ ④ ♦ ✈ ② Ó Ô Õ ♦ × ✇ ② × Ú ❣ ⑤ ♥ ② Ö Ø Ò Ø Ó Ô Õ ♦ ➇ ➐ ➬ t ♦ ✈ ② ⑥ ⑧ ④ ♦ ⑨ q ♣ ❣ s ✉ ⑦ ✈ ✇ ✈ ② ④ ♦ r ❣ st✉✈ q ⑨ ② ④ ④ ⑥ ① ⑨ s t ✉ ✈ ✇ ✈ ② ④ ♦ r ❣ st✉✈ q ② ② ④ ♦ ① ❣ st✉✈ q ⑨ ② ❣ ⑤ ④ ❣ st✉✈ ♦ ❣ ♣ ■ ❏ ❆ ❑ ▲ ▼ ◆ ◆❖ P ◗ ✻ ❘ ❙ ✽ ▼ ✿ ❚ ❱ ❲ ❳ ❀ ✽❨ ❲ ❬ ❲ ❞ ✁ ✝ ❢ ■ ❉❍ st✉✈ ✼ q ⑨ ② ✺ ✻✼✽✾ ✿ ❀❁ ❂❃ ❁ ❄ ❅❆ ✾ ✽ ❇ ● ❈ ❄ ❉ ❊ ❋ ✼ ✼ ✽ ❅ ❅ ✻ ❀ ✾ ❣ q ✄ ① r ❣ st✉✈ ✇ ① ❣ st✉✈ ♦ r ❣ st✉✈ ✇ ❣ ♥ s t ✉ ✈ ② ❣ ⑤ ♥ ✇ r ❣ s t ✇ ❣ ✈ ✄ ✌ ✄ ✌ ✁ ✞ ✌ ❧ ♠ ✌ ✁ ✝ ❢ ✌ ☛ ② ✂ ✟ ☎ ✁ ♥ q r ❣ st✉✈ ✇ ① ❣ st✉✈ ✉ ✇ ⑨ ⑥ ✈ ✇ ① ❣ s t ✉ ✈ ② ❣ ⑤ ⑥ ⑦ ⑧ ❣ ④ ❣ s t ✉ ✈ ② ④ ♦ ✈ ② ④ ♦ st✉ r ① ⑨ ❣ st✉✈ ② ❣ ⑤ ⑥ ⑦ ⑥ ⑧ ♥ ✇ ✈ ✇ ✇ q r ❣ st✉ ✈ ✇ ① ❣ st✉✈ ② ④ ❣ st✉ ✈ ✌ ❉❯ ☛ ➨ ➝ → ➣ ➜ ❼❽ ❾ ❿➀ ➁ ➂➃ ➀ ➆ ➨ ➭ ➯➲➳➵ ➊ ➍ ➊➎➏ ➍➐ ➑ ➒ ➟ ❼ ❿➸ ➃➺ ➀ ➄ ➯➲ ➇ ❾ ❿➀ ➁ ➂➃ ➀ ➆ ➨ ➨ ➩ ➂ ➁ ➋ ➨ ➌ ➊ ➍ ✂ ➎ ➏ ➍➐ ➫ ➅ ➁ ❿ ➂ ➻ ➳➵ ➞ ➹ ➊ ➐ ➍ ➊ ➎ ➏ ➍ ➐ ➪ → ➶ ➪ ➎ ➘ ➜ ❼❽ ❾ ❿ ➀ ➁ ➂➃ ➀ ➆ ➨ ➨ ➤ ➊ ➎ ➠ ➤ ➊ ➐ ➍ ➊➎➏ ➍➐ ➊ ➼ ➑ ➊ ➧ ➽ ➚ ➞ ➾ ➄ ➁ ➇ ➃ ➯➲ ➳ ➵ ➒ ➟ ➽ ❼❽ ➊ ➜ ➎ ➋➌ ➍ ➊➎➏ ➍➐ ➑ ➉ ➒ ➐ ➦ ➏ ➑ ➉ ➉ ➊ ➋ ➌ ➔ ↔ ↕ ➙ ➙ ➙ ↕ ➊ ➈ ➛ ⑩ ✟ ☎ ✁ ☛ ☞ ✍ ☎ ✄ ✟ ✂ ❢ ➇ ❶ ② ❶ ② ❼❽ ❾ ❿➀ ➁ ➂➃➄ ➅ ❽➆ ➣ ➓ ➜ ➠ ➊➡➢ ➤ ➥ ➦ ➉ ➧ ➝ ➠ ➊ ➥ ➦ ➉ ➝ → ➥ ➍ á ➉ ➜ → ➟ ➞ ➉ storing intermediate results ( factors ) to avoid recomputation Variable elimination: carry out summations right-to-left, Enumeration is inefficient: repeated computation Rewrite full joint entries using product of CPT entries: Simple query on the burglary network: structing its explicit representation Slightly intelligent way to sum out variables from the joint without actually con- ♦❫♣ ♦❫♣ ♦❫♣ e.g., computes ♦❫♣ ♦❫♣ ♦❫♣ ♦❫♣ ♦❫♣ ♦❫♣ ♦❫♣ ♦❫♣ ②ÜÛ ②③❫④ ♠❒❐ ÖÙØ (sum out (sum out ) for each value of ) Multiply connected networks: Singly connected networks (or polytrees ): Exhaustive depth-first enumeration: – equivalent to counting 3SAT models – can reduce 3SAT to exact inference – time and space cost of variable elimination are – any two nodes are connected by at most one (undirected) path extend : , evidence specified as an event , a belief network specifying joint distribution , the query variable has value a distribution over value ( where with value ( ( ) ( of , , ) ( in ) , is ) extended with for →❸➴ ) ( →❸➴ ➜❸➷ 1.0 a real number ♦❸❷ ➜❸➷ a distribution over [ ], ) space, ♦❸❹❻❺ →❸➣ NP-hard #P-complete ♦❸❹❻ß ( time ( ( ( ), ) ), )
Recommend
More recommend
![Faculty/Presenter Disclosure Faculty: [Speakers name] Relationships with commercial](https://c.sambuz.com/802839/faculty-presenter-disclosure-s.jpg)
