. . . x 1 x 1 x 2 x 2 x 3 x 3 x n x n 31 32 3-satisfiability - PowerPoint PPT Presentation

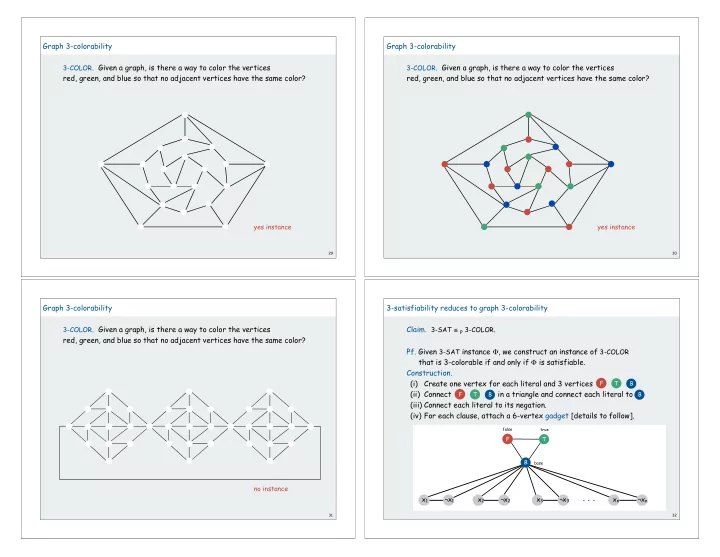
Graph 3-colorability Graph 3-colorability 3-COLOR . Given a graph, is there a way to color the vertices 3-COLOR . Given a graph, is there a way to color the vertices red, green, and blue so that no adjacent vertices have the same color? red, green, and blue so that no adjacent vertices have the same color? yes instance yes instance 29 30 Graph 3-colorability 3-satisfiability reduces to graph 3-colorability 3-COLOR . Given a graph, is there a way to color the vertices Claim. 3-SAT � P 3-COLOR . red, green, and blue so that no adjacent vertices have the same color? Pf. Given 3-SAT instance � , we construct an instance of 3-COLOR that is 3-colorable if and only if � is satisfiable. Construction. (i) Create one vertex for each literal and 3 vertices F T B (ii) Connect in a triangle and connect each literal to B. F T B B (iii) Connect each literal to its negation. (iv) For each clause, attach a 6-vertex gadget [details to follow]. false true F T B base no instance . . . x 1 ¬x 1 x 2 ¬x 2 x 3 ¬x 3 x n ¬x n 31 32

3-satisfiability reduces to graph 3-colorability 3-satisfiability reduces to graph 3-colorability Claim. If graph is 3-colorable then � is satisfiable.. Claim. If graph is 3-colorable then � is satisfiable.. Pf. Pf. � Suppose graph is 3-colorable. • Consider assignment where corresponds to false and to true . • Consider assignment where corresponds to false and to true . F T F T • (ii) [triangle] ensures each literal is true or false. • (ii) [triangle] ensures each literal is true or false. • (iii) ensures a literal and its negation are opposites. false false true true F T F T B B base base . . . . . . x 1 ¬x 1 x 2 ¬x 2 x 3 ¬x 3 x n ¬x n x 1 ¬x 1 x 2 ¬x 2 x 3 ¬x 3 x n ¬x n 33 34 3-satisfiability reduces to graph 3-colorability 3-satisfiability reduces to graph 3-colorability Claim. If graph is 3-colorable then � is satisfiable. Claim. If graph is 3-colorable then � is satisfiable. Pf. Pf. • Consider assignment where corresponds to false and to true . • Consider assignment where corresponds to false and to true . F T F F • (ii) [triangle] ensures each literal is true or false. • (ii) [triangle] ensures each literal is true or false. • (iii) ensures a literal and its negation are opposites. • (iii) ensures a literal and its negation are opposites. • (iv) [gadget] ensures at least one literal in each clause is true. • (iv) [gadget] ensures at least one literal in each clause is true. Therefore, � is satisfiable. stay tuned B B (x 1 � ¬x 2 � x 3 ) (x 1 � ¬x 2 � x 3 ) x 3 x 3 x 1 ¬x 2 x 1 ¬x 2 T 6-node gadget 6-node gadget F ?? T T F true false true false 35 36

3-satisfiability reduces to graph 3-colorability 3-satisfiability reduces to graph 3-colorability Claim. If � is satisfiable then graph is 3-colorable. Claim. If � is satisfiable then graph is 3-colorable. at least one in each clause Pf. Pf. • Color nodes corresponding to false literals T and to true literals F . • Color nodes corresponding to false literals T and to true literals F . • Color vertex below one T vertex F , and vertex below that B . (x 1 � ¬x 2 � x 3 ) x 3 x 3 x 1 ¬x 2 x 1 ¬x 2 T 37 38 3-satisfiability reduces to graph 3-colorability 3-satisfiability reduces to graph 3-colorability Claim. If � is satisfiable then graph is 3-colorable. Claim. If � is satisfiable then graph is 3-colorable. Pf. Pf. • Color nodes corresponding to false literals T and to true literals F . • Color nodes corresponding to false literals T and to true literals F . • Color vertex below one T vertex F , and vertex below that B . • Color vertex below one T vertex F , and vertex below that B . • Color remaining middle row vertices B . • Color remaining middle row vertices B . • Color remaining bottom vertices T or F as forced. Works for all gadgets, so graph is 3-colorable. � (x 1 � ¬x 2 � x 3 ) (x 1 � ¬x 2 � x 3 ) x 3 x 3 x 1 ¬x 2 x 1 ¬x 2 T 39 40

3-satisfiability reduces to graph 3-colorability Claim. 3-SAT � P 3-COLOR . Pf. Given 3-SAT instance � , we construct an instance of 3-COLOR that is 3-colorable if and only if � is satisfiable. Construction. (i) Create one vertex for each literal. (ii) Create 3 new vertices T, F, and B; connect them in a triangle, � designing algorithms and connect each literal to B. � proving limits (iii) Connect each literal to its negation. (iv) For each clause, attach a gadget of 6 vertices and 13 edges � classifying problems � polynomial-time reductions Conjecture: No polynomial-time algorithm for 3-SAT � NP-completeness Implication: No polynomial-time algorithm for 3-COLOR. Reminder Construction is not intended for use, just to prove 3-COLOR difficult 41 42 More Poly-Time Reductions Implications of Karp + Cook All of these problems poly-reduce to one another! 3-SAT 3-SAT 3-SAT 3-COLOR reduces to 3-SAT reduces to 3-COLOR reduces to 3-COLOR 3-SAT Dick Karp 3-COLOR 3DM VERTEX COVER 3-COLOR 3DM VERTEX COVER '85 Turing award PLANAR-3-COLOR HAM-CYCLE PLANAR-3-COLOR HAM-CYCLE EXACT COVER CLIQUE EXACT COVER CLIQUE SUBSET-SUM INDEPENDENT SET TSP HAM-PATH SUBSET-SUM INDEPENDENT SET TSP HAM-PATH PARTITION INTEGER PROGRAMMING PARTITION INTEGER PROGRAMMING Conjecture: no poly-time algorithm for 3-SAT. Conjecture: no poly-time algorithm for 3-SAT. KNAPSACK BIN-PACKING KNAPSACK BIN-PACKING (and hence none of these problems) (and hence none of these problems) 43 46

Poly-Time Reductions: Implications Poly-Time Reductions: Implications 47 48 Poly-Time Reductions: Implications 49